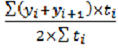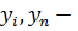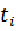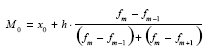Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя гармоническая простая и взвешенная.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Средняя гармоническая - используется, когда статистическая информация не содержит данных о весах по отдельным вариантам совокупности, но известны произведения значений варьирующего признака на соответствующие им веса. Общая формула средней гармонической взвешенной имеет следующий вид:
х – величина варьирующего признака, w – произведение значения варьирующего признака на его веса (xf) В том случае, если общие объемы явлений, т.е. произведения значений признаков на их веса равны, то применяется средняя гармоническая простая:
х – отдельные значения признака (варианты), n – общее число вариант. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия. 20. Средняя геометрическая и средняя хронологическая. Средняя геометрическая Если имеется n коэффициентов роста, то формула среднего коэффициента:
Это формула средней геометрической. Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего. Средняя хронологическая - средняя, рассчитанная из значений, изменяющихся во времени. Используется для расчета среднего уровня моментного ряда. В том случае, если имеющиеся данные относятся к фиксированным моментам времени c равными интервалами, то используется следующая формула:
Х – значение уровней ряда, n – число имеющихся показателей. Средний уровень моментных рядов динамики с неравноотстоящими датами определяется по формуле средней хронологической взвешенной:
, где
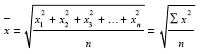
Средняя квадратическая. Взаимосвязь степенных средних величин. Если осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Например, с помощью средней квадратической можно определить диаметры труб, колес и т. д. Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число.
Средняя квадратическая взвешенная равна:
Понятие моды. Расчет моды для дискретного и интервального рядов распределения. Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана. Мода (Мо) – чаще всего встречающийся вариант. Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений. Мода представляет наиболее часто встречающееся или типичное значение. Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен. В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность). В пределах интервала надо найти то значение признака, которое является модой.
где хо – нижняя граница модального интервала; h – величина модального интервала; fm – частота модального интервала; fт—1 – частота интервала, предшествующего модальному; fm+1 – частота интервала, следующего за модальным. Мода зависит от величины групп, от точного положения границ групп. Мода – число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя).
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1932; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

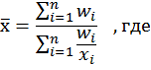
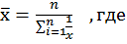
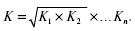
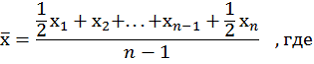
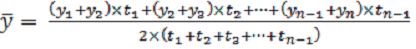 =
=