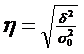Средняя гармоническая и средняя геометрическая, методы их расчета

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т. е. характеризует средний коэффициент роста.

Средняя геометрическая (простая):

Средняя геометрическая (взвешенная):

Средняя гармоническая

Определяющее свойство средней гармонической заключается в том, чтобы при осреднении оставалась неизменной сумма величин, обратных осредняемым.

 

 

Простая Взвешенная

Мода в дискретных и интервальных вариационных рядах

Модой- это варианта которая чаще всего встречается в данной совокупности.

В вариационном ряду-это будет варианта кот.имеет наибольшую частоту.

Мода в дискр. И интерв. Рядах определ. по разному. Мода в дискр. Ряду находится непосредственно по определению.

Сначала опр-ся мод интервал по наибольшей частоте, а затем по формуле:

х-minграница мод.интервала,fmo-частота мод.инт,fmo-1-предшеств инт,плюс 1- следующий инт

 

 

Медиана в дискретных и интервальных вариационных рядах

Медиана- наход.в серед. Вариационого ряда.Медиана делит ряд пополам.

Медиана в дискрет. и интерв.рядах определ. По разному. Медиана в дискр ряду находится непосредственно определению на основе накопленных частот. Медиана находится там, где накопл. Част. Равна или превышает полусумму частот.

Медиана в интервальных рядах аналогично опред номер медианы и медианый интервал.

Хme-minграница мед интервала,i-величина интервала,Sme-нак.частота интервала предшеств медианному.

Показатели вариации и способы их расчета

Простые взвешенные

Размах вариации

среднее линейное откл

дисперсия абс

среднеквадратичное

Коэф вариации

Правило сложения дисперсии и его применение в корреляционном анализе

Показатели вариации могут быть использованы не только в анализе изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями.

При проведении такого анализа совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным и результативным.

Для выявления взаимосвязи исходная совокупность делится на две или более групп по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:

- общая дисперсия;

- средняя из внутригрупповых дисперсий;

- межгрупповая дисперсия.

Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней:

Если факторный признак, по которому производится группировка, не оказывает никакого влияния на результативный признак, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая средняя будет равна нулю.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака фактора, положенного в основание группировки.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:

 

 

Эмпирический коэффициент детерминации представляет собой долю межгрупповой дисперсии в общей дисперсии.

Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.