
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахункова схема будівлі (споруди)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Література: [1, с. 6–21]; [3, с. 3–6]; [4, с. 9–12]; [5, с. 8–12]. Основні поняття та ключові слова розділу: реальний об’єкт, розрахункова схема, стержневі (дискретні) й суцільні (континуальні) системи, види навантажень і впливів, типи опор, проліт (прогін), розпір, стріла підйому, балка, рама, криволінійний брус, арка, ферма (стояк, розкіс, верхній та нижній пояс, панель). Методичні вказівки Інженерні споруди являють собою сукупність різних конструктивних елементів (стержнів, балок, плит, оболонок тощо), з'єднаних між собою у вузлах в'язями. Для розрахунку споруд необхідно визначити розрахункову схему, в якій окремі елементи споруди заміняють їх ідеалізованими схемами. При цьому відкидають ті другорядні фактори, що суттєво не впливають на роботу системи в цілому. Такі спрощення необхідні, оскільки без них розрахунок споруди є принципово неможливим через невичерпаність властивостей споруди. Спрощуються геометричні форми, фізико-механічні властивості матеріалу, характер навантаження тощо. Розрахункові схеми, в яких початкова та деформована форми збігаються з площиною, називаються плоскими. Крім того, є просторові системи, котрі при навантаженні відзначаються просторовим характером деформації. Вибір розрахункової схеми є важливим етапом розрахунку будівель і споруд (надалі – систем). При цьому необхідно знати, що від вдалого вибору розрахункової схеми споруди залежить трудомісткість i точність розрахунку. Потрібно засвоїти, яким чином прикріпляються елементи системи до основи, які бувають типи вузлів та опор; що являють собою шарнірно-рухома, шарнірно-нерухома, пружно-податлива, затиснута й затиснуто-рухома опори, скільки вони мають кінематичних в'язей. Запитання для самоконтролю 1. Яка схема називається розрахунковою? 2. Які спрощення приймаються при виборі розрахункових схем реальних об’єктів? 3. Назвіть і накресліть види опор. 4. Скільки кінематичних в’язей має кожний окремий вид опори? 5. Яка опора називається пружно-податливою? 2.3 Кінематичний аналіз розрахункових схем будівель (споруд) Література: [1, с. 28–46]; [2, с. 16–26]; [3, с. 6–13]; [4, с. 12–32, 45–51]; Основні поняття та ключові слова розділу: ступінь вільності системи, аналіз геометричної структури розрахункової схеми, геометрично змінна система (механізм), геометрично незмінна система, миттєво змінна система, статично визначувана й статично невизначувана система, шарнірно-стержнева та дискова система, диск, стержень, простий шарнір, кратний шарнір, опорна в’язь, опора, замкнений контур, вузол. Методичні вказівки Будівельні споруди мають бути нерухомими, тобто геометрично незмінними. Для визначення нерухомості розрахункової схеми виконують її кінематичний аналіз, який складається з розрахунку ступеня вільності W та аналізу її геометричної структури. Ступінь вільності W розрахункової схеми – кількість незалежних геометричних параметрів, що характеризують переміщення системи на площині або у просторі. Якщо плоска система складається з дисків Д, об'єднаних між собою простими шарнірами Ш, і опирається на нерухому основу за допомогою опорних в'язей Во, то кількість ступенів вільності W такої системи обчислюється за формулою W = 3Д – 2Ш - Во. (1) Необхідно звернути увагу на підрахунок кількості простих шарнірів. При цьому треба засвоїти, що шарнір, який з'єднує не два, а n дисків, називається кратним і дорівнює кількості n - 1 простих шарнірів. Крім того, потрібно мати на увазі, що диск - це така частина системи, геометрична незмінність якої раніше вже встановлена. Сам по собі диск може бути статично невизначуваний (наприклад, замкнений контур). При обчисленні ступеня вільності для шарнірно-стержневих систем доречно використовувати формулу W = 2В - С – Во, (2) де В – кількості вузлів; С – кількість стержнів. У випадку, коли W = 0, система буде статично визначуваною за умови її геометричної незмінності. При W < 0 система є статично невизначуваною і може бути геометрично незмінною. Установлення геометричної незмінності системи є важливим етапом кінематичного аналізу. Для цього необхідно вивчити закони утворення незмінних систем, засвоїти поняття про миттєву змінність та її характерні ознаки. Запитання для самоконтролю 1. Яка мета кінематичного аналізу розрахункових схем систем? 2. Які складові кінематичного аналізу? 3. Що називається ступенем вільності системи? 4. Як визначити ступінь вільності для дискових систем? 5. Простий і кратний шарніри. Як обчислюється кратність шарніра? 6. Як визначити ступінь вільності для шарнірно-стержневих систем? 7. Як довести, що система статично визначувана або невизначувана? 8. Чому необхідно виконувати аналіз геометричної структури розрахункової схеми? 9. Правила утворення незмінних систем. Випадки миттєвої змінності. Статично визначувані стержневі системи Методи визначення зусиль від нерухомого навантаження в статично визначуваних системах Література: [1, с. 98–120]; [2, с. 27–31, 51–59, 62–64]; [3, с. 14–17]; [4, с. 33–45]; [5, с. 25–28]. Основні поняття та ключові слова розділу: зовнішнє навантаження, зосереджена сила, розподілене навантаження, зосереджений момент, опорні реакції, епюра, внутрішні зусилля, згинальний момент, поперечна сила, поздовжня сила, принцип суперпозиції (незалежності дії), переміщення (кутові, лінійні). Методичні вказівки Основні дані про навантаження й визначення внутрішніх зусиль уже відомі з курсу опору матеріалів. У цьому розділі необхідно засвоїти класифікацію навантажень залежно від тривалості їх дії. Згідно з діючими нормативними документами навантаження класифікуються як постійні та тимчасові (тривалі, короткочасні, особливі тощо). Розпочинаючи розрахунок статично визначних систем, необхідно повторити метод перерізів, правила побудови епюр внутрішніх зусиль, залежність між навантаженнями і зусиллями. Запитання для самоконтролю 1. Види навантажень. Їх класифікація згідно із чинними нормативними документами. 2. Які внутрішні зусилля можуть виникати в перерізі стержневої системи при дії навантажень та інших впливів? 3. Що називається епюрою? 4. Правила побудови епюр внутрішніх зусиль і їх перевірки. 5. У чому полягає принцип незалежності дії сил (принцип суперпозиції)? Тришарнірні системи Література: [1, с. 182–200]; [2, с. 70–82, 87–95]; [3, с. 65–72]; [4, с. 126–144]; [5, с. 50–58]. Основні поняття та ключові слова розділу: тришарнірна система (арка, рама), ключовий шарнір, опорний шарнір, розпір, раціональне окреслення осі арки, затяжка (затяг), прогін арки, стріла підйому арки. Методичні вказівки При вивченні даної теми необхідно засвоїти, які системи називаються тришарнірними, та вивчити їх класифікацію. Особливу увагу слід звернути на те, що при дії на тришарнірну систему вертикального навантаження в її опорах виникають не тільки вертикальні, але й горизонтальні опорні реакції (розпір). Для визначення розпору необхідно скласти рівняння статики, які ґрунтуються на рівності нулю згинального моменту в ключовому шарнірі тришарнірної системи. Потрібно також вивчити способи визначення внутрішніх зусиль у перерізах тришарнірної системи від довільного навантаження. При вертикальному навантаженні на тришарнірну систему внутрішні зусилля можна визначати за формулами:
Необхідно знати, як одержані ці формули і їх зміст, а також вивчити питання про раціональне окреслення осей арок. Вивчаючи тришарнірні системи із затяжкою, слід засвоїти, що являє собою затяжка i для чого вона призначена, а також ознайомитися зі способами визначення в ній поздовжнього зусилля. Особливості розрахунку тришарнірних рам. Розрахунок тришарнірної рами необхідно починати з кінематичного аналізу (визначення ступеня вільності W та аналізу геометричної структури заданої розрахункової схеми). Наступним кроком є визначення складових опорних реакцій. Опорні реакції обчислюються в такій послідовності:
де А та В - опорні шарніри; С - ключовий шарнір. Для побудови епюр М, Q і N необхідно скласти рівняння цих зусиль на ділянках рами залежно від розташування перерізу (х). Задаючись різними значеннями аргументу (х), отримують величини згинальних моментів, поперечних та поздовжніх сил у перерізах на ділянках рами, згідно з якими будуються епюри М, Q і N. Статична перевірка епюри М виконується шляхом розгляду рівноваги жорстких вузлів рами. Епюри Q та N перевіряються сумісно, шляхом розгляду рівноваги вузлів рами або будь-якої відсіченої її частини (сума проекцій усіх зовнішніх i внутрішніх сил відсіченої частини рами на вертикальну та горизонтальну осі повинна дорівнювати нулю). Запитання для самоконтролю 1. Яка система називається тришарнірною? 2. Як виконати кінематичний аналіз тришарнірних систем? 3. Які існують види тришарнірних систем? 4. Що являє собою розпір тришарнірної системи? 5. Яке призначення затяжки у тришарнірних системах? 6. Як визначаються опорні реакції тришарнірних систем та виконується перевірка їх обчислень? 7. Як визначаються внутрішні зусилля у тришарнірних системах при довільному навантаженні? 8. Які особливості обчислення внутрішніх зусиль у тришарнірних системах при вертикальному навантаженні? 9. Яке окреслення осі арки є раціональним?
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 705; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.63 (0.008 с.) |

 ; (3)
; (3)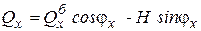 ; (4)
; (4) . (5)
. (5)


 ,
,


