Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вибір основної системи методу сил. Канонічні рівняння методу силСодержание книги
Поиск на нашем сайте
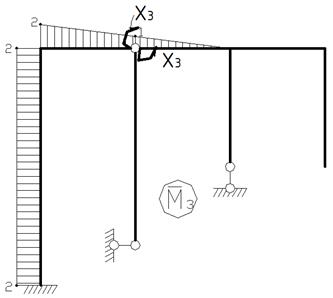
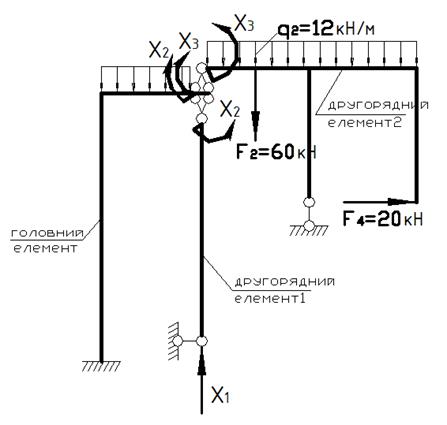
Основну систему методу сил (ОСМС) вибираємо шляхом відкидання зайвих в’язей, навантаживши при цьому її зовнішніми силами та зусиллями відкинутих зайвих в’язей Х1, Х2, Х3. Х1, Х2, Х3 – основні невідомі методу сил.
Поверхова схема основної системи методу сил має такий вигляд:
Для основної системи методу сил запишемо канонічні рівняння у вигляді системи лінійних алгебраїчних неоднорідних рівнянь:
Зміст канонічних рівнянь: – першого – переміщення перерізу, де прикладена невідома Х1 у напрямку невідомої Х1, від основних невідомих і зовнішнього навантаження дорівнює нулю; – другого – переміщення перерізів, де прикладені невідомі Х2 у напрямку невідомих Х2, від основних невідомих і зовнішнього навантаження дорівнює нулю; – третього – переміщення перерізів, де прикладені невідомі Х3 у напрямку невідомих Х3, від основних невідомих і зовнішнього навантаження дорівнює нулю. У матричному вигляді система має вигляд:
де
2.4. Побудова в основній системі епюр згинальних моментів від Епюри згинальних моментів від одиничних значень основних невідомих.
Для перевірки коефіцієнтів та вільних членів канонічних рівнянь методу сил виконуємо побудову одиничної епюри моментів від сумісної дії Х1=1, Х2=1, Х3=1 за формулою
Епюра згинальних моментів в осно
2.5. Обчислення коефіцієнтів матриці податливості, вектора Коефіцієнти канонічних рівнянь методу сил (матриці податливості) визначаємо за формулою
Отже, маємо Перевірка коефіцієнтів матриці податливості
Отже, коефіцієнти матриці податливості обчислені правильно. Вільні члени канонічних рівнянь методу сил (вектор вільних членів) визначаються за формулою
де
Перевірка вільних членів канонічних рівнянь методу сил
Отже, вільні члени канонічних рівнянь методу сил обчислені правильно. 2.6. Розв’язок системи канонічних рівнянь методу сил, Система канонічних рівнянь методу сил має вигляд:
Після розв'язування системи одержимо
Перевірка розв'язування системи канонічних рівнянь методу сил
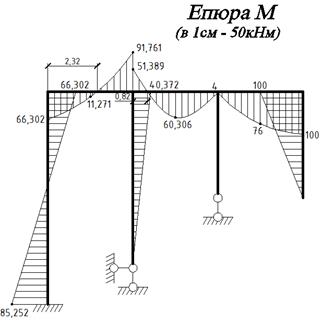
2.7. Побудова епюр внутрішніх зусиль для заданої системи, 1. Побудова епюри згинальних моментів Згідно з принципом суперпозиції, епюру згинальних моментів М для заданої системи будуємо таким чином:
а) кінематична перевірка епюри згинаючих моментів для заданої системи
Відносна похибка: Висновок: епюру Mх побудовано правильно. б) статична перевірка епюри згинальних моментів для заданої системи
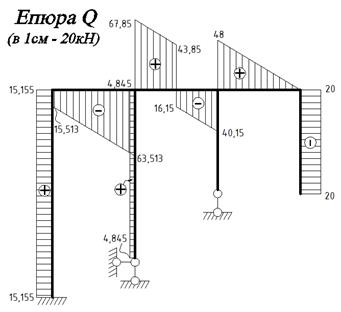
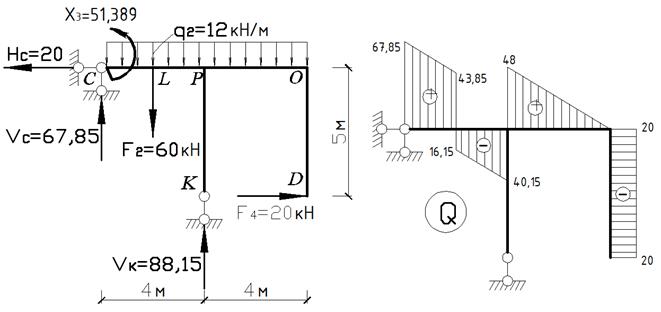
2. Побудова епюри поперечних зусиль Епюру поперечних зусиль Q будуємо з використанням епюри згинальних моментів для заданої системи, розглядаючи окремо кожний її елемент.
Елемент DCК Опорні реакції
Перевірка:
Ділянка DO:
Ділянка CL:
Елемент BC Опорні реакції:
Ділянка BC:
Елемент AЕC Ділянка CE:
Ділянка EA:
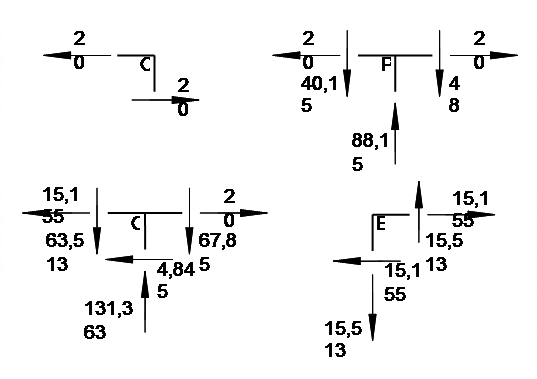
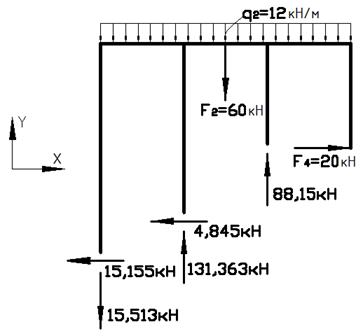
Отже, епюра Q для заданої системи буде мати такий вигляд:
3. Побудова епюри поздовжніх зусиль Епюру поздовжніх зусиль N будуємо шляхом використання умов рівноваги окремих вузлів системи
У результаті розрахунків отримаємо епюру N для заданої системи.
4. Загальна статична перевірка заданої системи
Висновок. Задана система знаходиться в рівновазі, епюри Q та N побудовано правильно.
Література 1. Смирнов А.Ф., Александров А.В., Лащеников Б.Я., Шапошников Н.Н. Строительная механика стержневых систем. – М.: Стройиздат, 1981. 2. Дарков А.В., Шапошников Н.Н. Строительная механика. – 8-е изд., перераб. и доп. – М.: Высшая школа, 1986. 3. Киселев В.А. Строительная механика, общий курс – 4-е изд., исправленное и доп. – М.: Стройиздат, 1986. 4. Бутенко Ю.И., Канн С.Н., Пустовойтов В.П. и др. Строительная механика стержневых систем и оболочек. – К.: Вища школа, 1980. 5. Строительная механика. Руководство к практическим занятиям / Под ред. Ю.И. Бутенко. – К.: Вища школа, 1989. 6. Руководство к практическим занятиям по курсу строительной механики (статически определимые и неопределимые системы) / Под ред. Г.К. Клейна. – 7. Методичні вказівки із завданнями до виконання самостійної та розрахунково-графічної роботи з дисципліни “Будівельна механіка” для студентів усіх форм навчання спеціальності “Теплогазопостачання і вентиляція”. – Полтава: ПолтНТУ, 2011. – 58 с. Укладачі: О.А. Шкурупій, В.О. Северин, А.М. Пащенко, О.О. Голов.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.112.15 (0.006 с.) |





 ,
, – матриця податливості;
– матриця податливості; – вектор невідомих;
– вектор невідомих; – вектор вільних членів.
– вектор вільних членів.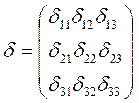 ;
; 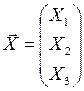 ;
;  .
.

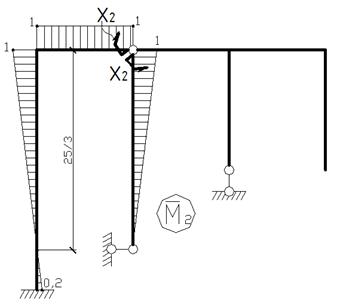




 .
.
 вній системі від заданого навантаження.
вній системі від заданого навантаження.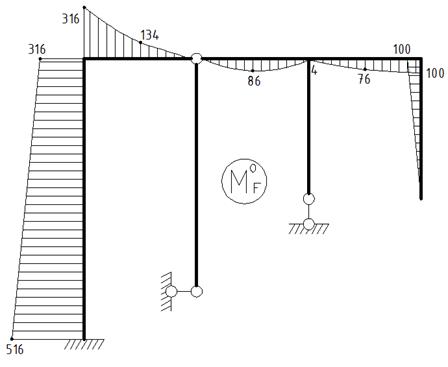
 ; i, k =1,2,3.
; i, k =1,2,3. ;
; ;
;  ;
;

 ;
;
 .
. .
.
 ;
;
 .
.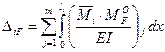 ,
, – епюра згинальних моментів в основній системі від заданого навантаження;
– епюра згинальних моментів в основній системі від заданого навантаження;
 ;
;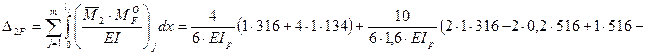
 ;
;
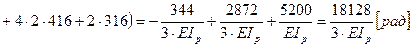 .
.
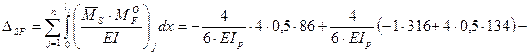
 ;
;  .
.
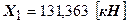 ;
; ;
; .
.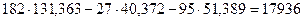 ;
; .
.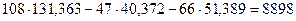 ;
; .
. ;
; .
.
 .
.




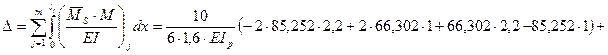

 .
. .
.

 ;
; ;
; ;
; .
.


 ;
; ;
; :
:  ;
; :
:  ;
; .
. :
: 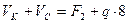 ;
; .
. Ділянка OP:
Ділянка OP: 
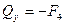 ;
;  ;
; .
.  ;
; .
. Ділянка OP:
Ділянка OP:  ;
;  ;
; ;
;  ;
; .
.  .
.


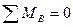 :
:  ;
; ;
; .
.
 ;
; .
.
 ;
;



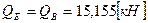




 ;
;  .
. ;
;  .
.