
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розподіл Максвелла-БольцманаСодержание книги
Поиск на нашем сайте
де Для знаходження функції
де
У лівій частині рівняння (3.2) стоятиме нуль за відсутності зіткнень електронів з іншими частинками чи квазічастинками у відповідності до теореми Ліувілля. Теорема стверджує: об’єм елемента фазового простору У реальному кристалі відбуваються процеси зіткнення електронів із фононами, дефектами, домішками та електронами і тому в правій частині замість нуля необхідно записати похідну змінної функції розподілу -
де Труднощі при розв’язанні (3.3) вимагають використання наближення часу релаксації, що дає можливість записати інтеграл зіткнень у вигляді
де f0 – локально і миттєво рівноважна функція розподілу (вона була б, якщо при даних Припущення (3.4) означає, що швидкість зміни числа частинок у даному стані пропорційна відмінності цього числа від того, яке б було за умови, що миттєві значення всіх параметрів, що впливають на нього, були б «заморожені», і мала б місце рівновага. Зміст самостійної роботи: Розглянути рисунок 3.1 та опрацювати матеріал про розмиття функції Фермі-Дірака Типи електропровідності Здатність твердих тіл пропускати електричний струм характеризується їх електричною провідністю або електропровідністю. Величина обернена електропровідності називається питомим опором. Чим більше в твердому тілі електронів, тим більшою є його електронна провідність. Чим більше в твердому тіле дірок, тем більшою є його діркова провідність. Однак, на величину електропровідності впливає не тільки концентрація вільних носіїв заряду, але і їх рухливість. Рухливість формально можна ввести як деякий коефіцієнт пропорційності між середньою швидкістю дрейфу носіїв заряду в електричному полі та величиною самого електричного поля: V=μE. Як видно з формули, μE має розмірність [см2/(В·с)]. Рухливість є тим вищою, чим рідше електрони або дірки зіштовхуються з атомами решітки, домішок чи дефектами. Співвідношення лежить в основі закону Ома, який встановлює пропорційність між струмом через взірець та напругою, прикладеною до нього:
В твердому тілі, яке поміщене в електричне поле, електрон бере участь в двох типах руху: хаотичному тепловому та напрямленому дрейфі під дією електричного поля (див. рисунок). Як видно з цього рисунка, середня швидкість і, відповідно, рухливість тим вища, чим є більшою довжина вільного пробігу і чим менша ефективна маса носіїв заряду (зменшення ефективної маси призводить до збільшення нахилу ліній на лівому рисунку). Рухливість слабо залежить від температури. Для нелегованих напівпровідників вона зменшується зі збільшенням температури пропорційно T-3/2. Тому електропровідність для нелегованих матеріалів визначається змінною концентрації, яка експоненційно зростає при зростанні температури. Залежність електропровідності від температури показана на правому рисунку. Як видно з графіків, чим є більшою ширина забороненої зони, тем менше абсолютне значення провідності, однак, тим сильніше провідність залежить від температури (більший нахил). В напівпровідниковій електроніці, головним чином, використовуються леговані матеріали. В легованих напівпроводниках домішка вносить додаткову концентрацію домішковихх носіїв заряду, котрі мають свою власну залежність від температури, яка накладується на температурну залежність власних носіїв заряду. В області високих температур, там, де домінують міжзонні переходи і власна концентрація носіїв є більшою за домішкову (ni>>nд), напівпровідник веде себе як власний (область I). В області низьких температур (область III), там де домішка не іонізована рівень Фермі повинен знаходитись вище донорного рівня (ймовірність заповнення електронами більше 1/2). По мірі того, як температура підвищується донори віддають електрони в зону віддали свої електрони, а концентрація власних електронів усе ще дуже мала, концентрація електронів в цій області залишається постійною і приблизно рівною концентрації домішкових атомів. Іменно ця температурна область і є основною областю роботи значної кількості напівпровідникових діодів та транзисторів. Рис.4.2.
Оскільки в області II концентрація носіїв змінюється в незначній мірі, то в електропровідності (крива В) стає замітним вклад рухливості, що призводить до деякого падіння електропровідності зі зростанням температури (що взагалі не характерно для напівпровідників) в деякому інтервалі температур за рахунок домінування розсіяння на коливаннях решітки. Потім з підвищенням температури відбувається перехід до власної провідності, концентрація електронів та електропровідність починають зростати за експоненційним законом зі зростанням температури. Зміст самостійної роботи: Опрацювати матеріал про області високих за допомогою рисунка 4.2.
|
||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.130.151 (0.01 с.) |

 У стані рівноваги всі вільні електрони беруть участь у невпорядкованому тепловому русі. При цьому, виходячи із симетрії функції розподілу, кількість електронів, що рухаються у протилежних напрямках, однакова, а, отже, макроскопічні електричні струми відсутні. Якщо до зразка прикладено електричне поле, то, рухаючись під його дією, електрон набуде не тільки додаткової швидкості
У стані рівноваги всі вільні електрони беруть участь у невпорядкованому тепловому русі. При цьому, виходячи із симетрії функції розподілу, кількість електронів, що рухаються у протилежних напрямках, однакова, а, отже, макроскопічні електричні струми відсутні. Якщо до зразка прикладено електричне поле, то, рухаючись під його дією, електрон набуде не тільки додаткової швидкості  , а й додаткової енергії
, а й додаткової енергії  . Якби ніякі процеси не перешкоджали збільшенню швидкості електрона, то вона нескінченно б зростала. Але в дійсності електрони час від часу зіштовхуються один з одним, з фононами та дефектами. У зв’язку з цими процесами було введено величину
. Якби ніякі процеси не перешкоджали збільшенню швидкості електрона, то вона нескінченно б зростала. Але в дійсності електрони час від часу зіштовхуються один з одним, з фононами та дефектами. У зв’язку з цими процесами було введено величину  - середній час релаксації, час впродовж якого електрон безперешкодно прискорюється. Отже, для того щоб підтримувався стаціонарний стан, необхідне існування таких зіткнень, при яких електрон міг би втрачати не тільки імпульс, а й додаткову енергію. Зіткнення першого типу (тобто без значних втрат енергії) називаються пружними, другого – непружними. Розгляд цих процесів показав, що можливі два типи майже пружних зіткнень електронів – з дефектами і акустичними фононами і два непружних – з оптичними фононами та міжелектронні, які відіграють суттєву роль лише в обмеженому інтервалі температур і концентрацій. Отже, рівнянь напівкласичної динаміки виявилося недостатнім для розрахунку інтегральних характеристик твердого тіла, які визначаються блохівськими електронами, - провідності, потоку тепла та ін. Необхідно знати ще нерівноважну функцію розподілу
- середній час релаксації, час впродовж якого електрон безперешкодно прискорюється. Отже, для того щоб підтримувався стаціонарний стан, необхідне існування таких зіткнень, при яких електрон міг би втрачати не тільки імпульс, а й додаткову енергію. Зіткнення першого типу (тобто без значних втрат енергії) називаються пружними, другого – непружними. Розгляд цих процесів показав, що можливі два типи майже пружних зіткнень електронів – з дефектами і акустичними фононами і два непружних – з оптичними фононами та міжелектронні, які відіграють суттєву роль лише в обмеженому інтервалі температур і концентрацій. Отже, рівнянь напівкласичної динаміки виявилося недостатнім для розрахунку інтегральних характеристик твердого тіла, які визначаються блохівськими електронами, - провідності, потоку тепла та ін. Необхідно знати ще нерівноважну функцію розподілу  , оскільки проходження струму - це нерівноважний процес. Функція
, оскільки проходження струму - це нерівноважний процес. Функція  -просторі (
-просторі ( -просторі), яка визначається так: середнє число електронів, що знаходяться у деякому нерівноважному стані з квазіімпульсом
-просторі), яка визначається так: середнє число електронів, що знаходяться у деякому нерівноважному стані з квазіімпульсом  в момент часу t, становить
в момент часу t, становить  . Якщо n -а енергетична зона заповнена повністю, то густина струму в ній (і потік енергії, яку переносять електрони) дорівнює нулю. Якщо n -а енергетична зона заповнена не повністю (наприклад, у металах), то густина струму в ній
. Якщо n -а енергетична зона заповнена повністю, то густина струму в ній (і потік енергії, яку переносять електрони) дорівнює нулю. Якщо n -а енергетична зона заповнена не повністю (наприклад, у металах), то густина струму в ній , (3.1.)
, (3.1.) - частка функції розподілу Фермі-Дірака, яка пов'язана лише із тими електронами, які беруть участь в електропровідності (їх енергетичні стани розміщуються у розмитті функції Фермі-Дірака, яка показана на рис. 3.1).
- частка функції розподілу Фермі-Дірака, яка пов'язана лише із тими електронами, які беруть участь в електропровідності (їх енергетичні стани розміщуються у розмитті функції Фермі-Дірака, яка показана на рис. 3.1).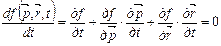 , (3.2)
, (3.2) - градієнт функції розподілу в напрямку
- градієнт функції розподілу в напрямку 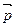 ;
;  - градієнт функції розподілу в напрямку
- градієнт функції розподілу в напрямку  .
.
 ; 3- при Т>0К і
; 3- при Т>0К і  ; 4 -
; 4 -  для кривої 2
для кривої 2
 зберігається під час руху, якщо відсутні зіткнення (тобто зберігається і число частинок), отже, функція розподілу залишається постійною, а
зберігається під час руху, якщо відсутні зіткнення (тобто зберігається і число частинок), отже, функція розподілу залишається постійною, а  .
. , яку Больцман назвав інтегралом зіткнень, оскільки при її обчисленні необхідно інтегрувати за всіма змінними, що впливають на імовірність зіткнень. Тоді кінетичне рівняння у самому загальному випадку запишеться так:
, яку Больцман назвав інтегралом зіткнень, оскільки при її обчисленні необхідно інтегрувати за всіма змінними, що впливають на імовірність зіткнень. Тоді кінетичне рівняння у самому загальному випадку запишеться так: , (3.3)
, (3.3) - сила, яка діє на електрон;
- сила, яка діє на електрон;  - середня швидкість дрейфу електрона у зовнішньому електричному полі.
- середня швидкість дрейфу електрона у зовнішньому електричному полі.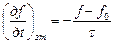 , (3.4)
, (3.4) мала б місце рівновага);
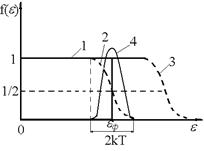
мала б місце рівновага);  - параметр, що визначає швидкість наближення до рівноваги (час релаксації),
- параметр, що визначає швидкість наближення до рівноваги (час релаксації),  .
.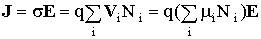
 Рис. 4.1.
Рис. 4.1. провідиності і поступово повністю іонізуються (область II). Область II прийнято називати областю спустошення домішки, оскільки усі атоми донорів
провідиності і поступово повністю іонізуються (область II). Область II прийнято називати областю спустошення домішки, оскільки усі атоми донорів


