
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
У чому перевага супутникового телебаченняСодержание книги
Поиск на нашем сайте
Особливості ультракоротких хвиль забезпечили їх широке застосування в супутниковому телебаченні. Супутникове телебачення — система передання телевізійного сигналу від передавального центра до споживача через штучний супутник Землі, розташований на геостаціонарній навколоземній орбіті. Із центральної керувальної станції на супутник передають високочастотний сигнал. Передавач, установлений на супутнику, передає цей сигнал на Землю. Приймальний пристрій складається із супутникової тарілки, конвертора, що знижує частоту прийнятого сигналу, і приймача. Перевагою супутникового телебачення є те, що можна приймати тисячі телевізійних каналів, перебуваючи на великій відстані від передавальних телевізійних центрів. Питання для самоконтролю: 1. На яких принципах базується робота радіолокатора? 2. Чому для радіолокації використовують електромагнітні хвилі дуже малої довжини? 3. Чому антена радіолокаційної станції обертається? 4. Радіохвилі якого діапазону використовують для телемовлення? 5. Чому стійкий прийом телевізійного передання можливий тільки в межах видимості випромінювальної антени? Зміст самостійної роботи: 1. Якісні питання 1. Чому радіолокаційна установка повинна надсилати радіосигнали у вигляді коротких імпульсів, що йдуть через рівні проміжки часу один за одним? 2. Який прилад у радіолокаційній установці служить для вимірювання часу між відправленням сигналу й прийомом відбитого імпульсу? 3. Чому дальність дії передавальної телевізійної станції обмежена лінією горизонту? 4. Навіщо передавальні антени телецентрів розташовують на багатометрових вишках? 2. Розв’яжіть задачі 1. Тривалість імпульсу радіолокатора tiмп = 2 мкс, а проміжок часу між імпульсами Δt = 0,6 мс. Визначте максимальну й мінімальну відстань визначення цілей цим радіолокатором. 2. Антена корабельного радіолокатора перебуває на висоті h = 20 м над водою. На якій найбільшій відстані цей радіолокатор може виявити вночі рятувальний пліт, якщо хвиль на море немає? Радіус Землі 6400 км.
Тема 5. Основи теорії твердого тіла План самостійної роботи до теми
Будова твердого тіла
Кристали – це тверді тіла, в яких атоми або молекули мають чітку тривимірну періодичність. Структурукристала можна зобразити як нескінченні симетричні ряди, сітки і решітки з періодично повторюваних частинок. Для характеристики внутрішньої структури кристалів користуються поняттям кристалічної решітки. Кристалічна решітка - періодична тривимірна структура, в якій атоми чи молекули займають фіксовані положення і перебувають на певних відстанях. Найбільш загальними макроскопічними властивостями кристалічної решітки є її однорідність, анізотропія і симетрія. Багатогранник, трансляціями якого можна без пропусків і перекривань повністю заповнити всю безкінечну решітку, називається елементарною коміркою. Вибір такої комірки неоднозначний. Наприклад, це може бути паралелепіпед, ребрами якого є основні трансляції. Довжини ребер називають постійними решітки. Елементарна комірка мінімально можливого об’єму називається примітивною елементарною коміркою. Вона може мати чи не мати всі елементи симетрії решітки. Зокрема, всі елементи симетрії решітки має примітивна елементарна комірка Вігнера-Зейтца. Вона будується так: будь-який вузол решітки (взятий за початковий) з’єднують відрізками з іншими вузлами, а потім через середини цих відрізків проводять площини, перпендикулярні до них. Багатогранники, обмежені цими площинами, утворюють комірку Вігнера-Зейтца (рис. 1.1).
Рис. 1.1. - Побудова елементарної комірки Вігнера-Зейтца (для двовимірної решітки)
Геометрична будова елементарних комірок характеризує кристалографічну структуру речовини. Тому за формою зручно класифікувати не кристали, а елементарні комірки. При цьому всі кристали поділяються на кристалографічні системи (сингонії) різних типів. Як і будь-який багатогранник, елементарна комірка (рис. 1.3) характеризується шістьма параметрами: довжинами ребер (
На основі кристалічних решіток, що відповідають різним кристалографічним системам, Н. Франкенгейм (1835р.), а потім О. Браве (1850р.) виділили 14 видів трансляційних решіток, які тепер називаються решітками Браве. Решіткою Браве називається система точок з радіусами-векторами
де Як видно із таблиці 1.1, кристалографічні сингонії Таблиця 1.1 - Типи кристалографічних сингоній та решіток Браве
об’єднують у собі чотирнадцять типів решіток Браве. Властивістю решітки Браве є те, що із будь-якої її точки весь (безкінечний) кристал «спостерігається однаково». Примітивна комірка може містити декілька (іноді дуже багато) атомів - різних або однакових, що знаходяться в нееквівалентних положеннях. Такі групи атомів називають базисом; говорять про одноатомний, двоатомний і т.д. базис.
У фізиці твердого тіла опис кристалів можна значно спростити, якщо ввести поняття оберненого простору і відповідно оберненої решітки. Визначити її можна таким чином: якщо система точок (1.1) — пряма решітка, то обернена решітка - це система точок
де n1, n2 та n3 – цілі числа; Слід також відмітити, що кожному вектору оберненої решітки Базисні вектори оберненої решітки визначаються через вектори прямої решітки:
де У випадку кубічної та інших прямокутних решіток
тобто вектори оберненої решітки визначаються через хвильові числа. Із цієї причини простір оберненої решітки може розглядатись як простір хвильових векторів (k -простір) або простір імпульсів (p -простір), оскільки імпульс
а б
Рис. 1.3 - Приклади зон Бриллюена для дво- (а) та тривимірної (б) решіток
Наступні зони Бриллюена будуються так: будь-який вузол оберненої решітки (взятий за початковий) з’єднують відрізками з іншими вузлами, а потім через середини цих відрізків проводять перпендикулярні площини. Багатогранники, обмежені цими площинами, утворюють зони Бриллюена. Об’єми всіх зон однакові.
Зміст самостійної роботи: Розв’яжіть задачу: Написати індекси напрямку прямої, яка проходить через вузли [[100]] та [[001]] примітивної кубічної решітки
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 776; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.52.109 (0.009 с.) |


 ,
,  ,
,  ) і кутами між ними (α, β, γ). Залежно від співвідношення між цими відрізками (сталими решітки) і кутами розрізняють сім кристалографічних систем (сингоній).
) і кутами між ними (α, β, γ). Залежно від співвідношення між цими відрізками (сталими решітки) і кутами розрізняють сім кристалографічних систем (сингоній). , (1.1)
, (1.1) ,
,  і
і  - основні вектори трансляцій; m1, m2 та m3 – цілі числа.
- основні вектори трансляцій; m1, m2 та m3 – цілі числа.
 і площина
і площина


 і площина
і площина















 , (1.2)
, (1.2) ,
,  ,
,  - основні вектори оберненої решітки.
- основні вектори оберненої решітки. відповідає сімейство атомних площин (в яких лежать точки прямої решітки), перпендикулярних до вектора
відповідає сімейство атомних площин (в яких лежать точки прямої решітки), перпендикулярних до вектора  , відстані між якими
, відстані між якими  , де Bmin –довжина найменшого вектора оберненої решітки, паралельного
, де Bmin –довжина найменшого вектора оберненої решітки, паралельного  .
. ,
,  ,
, 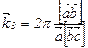 ,
, - об’єм елементарної комірки прямої решітки.
- об’єм елементарної комірки прямої решітки. ,
,  ,
,  ,
, . Елементарна комірка Вігнера-Зейтца в такому просторі являє собою першу зону Бриллюена. На рис. 1.6 наведено приклади побудови зон для двовимірної простої квадратної решітки (три зони) і для прямої ГЦК-решітки (перша зона).
. Елементарна комірка Вігнера-Зейтца в такому просторі являє собою першу зону Бриллюена. На рис. 1.6 наведено приклади побудови зон для двовимірної простої квадратної решітки (три зони) і для прямої ГЦК-решітки (перша зона).




