Особенности операций десятичной арифметики

Арифметические операции над десятичными числами (сло­жение, вычитание, умножение, деление) выполняются аналогич­но операциям над целыми двоичными числами. Основой АЛУ десятичной арифметики является сумматор двоично-деся­тичных кодов. Такой сумматор, как правило, строится на осно­ве двоичного путем добавления некоторых цепей.

Рассмотрим, каким образом можно выполнить сложение двоично-десятичных кодов. Пусть необходимо сложить модули двух двоично-десятичных чисел X и Y. Первое слагаемое X преобразуем в код с избытком 6 (обозначим Х6), полу­чаемый путем прибавления к каждой цифре X двоичного числа 6. Переход от X к Х6 изменяет все тетрады X так, что в каждой тетраде Х6 находится число 6 - 15.

Складывая Х6 и Y по правилам двоичного сложения, полу­чаем результат Z'. В Z' одни тетрады совпадают, а другие не совпадают с тетрадами двоично-десятичной суммы Z.

Если результат сложения в i-м разряде X [i] + Y[i] + Р [i] >= 10, где Р [i] - десятичный перенос в i-й разряд, то i-я десятичная цифра Z [i] = X [i] + Y[i] + Р [i] – 10 и Р [i + 1] = 1, где Р [i + 1] - десятичный перенос в (i + 1)-й разряд. Для Z'[i] в этом случае получаем

Z'[i] = Х6[1] + У[i] +P[i] - 16= 6+ X[i] + Y[i] + Р[i] - 16 = Z[i].

При этом возникает перенос в (i+1)-ю тетраду.

Если 1-я десятичная цифра Z(i) должна получаться из X [i] + Y[i] + Р [i] < 10, то Z[i] = X [i] + У[i] + Р [i] и Р[i+1] = 0.

Для Z'(i) в этом случае получаем

Z’[i] =X6[i] + Y[i] + Р[i] = 6 + Х[i] + У[i] + Р[i] =Z[i] + 6.

Перенос в (i + 1)-ю тетраду здесь не возникает (Р[i+1] = 0), так как

Z' [i] < 16.

Таким образом, складывая Х6 и Y как двоичные числа, по­лучаем Z'. В Z' тетрады, из которых возникал перенос, совпа­дают с тетрадами двоично-десятичного результата Z, а те­трады, из которых не было переноса при сложении, предста­влены с избытком 6. Для получения суммы Z необходимо откорректировать Z' путем уменьшения на 6 тех тетрад Z, из которых не было переноса при сложении Х6 и Y.

Вычитание числа 6 из тетрад, требующих коррекции, можно ре­ализовать путем подсуммирования числа 10 с одновременным игно­рированием переноса, возникающего при этом из тетрад. Если Z' [i] нуждается в коррекции, то Z' [i] = Z[i]+ 6. Поэтому Z'[i] + 10 >= 16, значит, после прибавления 10 из тетрады возни­кнет перенос, т. е. в тетраде останется (Z' [i] + 10)-16 = Z[i]-6.

Вычитание двоично-десятичных модулей X-Y осущест­вляется следующим образом.

Все разряды Y инвертируются, что дает дополнение каждой цифры Y до 15, при этом получается обратный код двоично-де­сятичного Y с избытком 6, обозначенный Уобр6. Затем, склады­вая X + Уобр6 и прибавляя 1 к младшему разряду, получаем Z. Результат Z' является положительным числом, если из старшей тетрады его возникает перенос, при этом Z' корректируется по тем же правилам, что и при сложении модулей.

Если из старшей тетрады 2' нет переноса, то получен отри­цательный результат, представленный в дополнительном коде. В этом случае код Z' инвертируется и к нему прибавляется 1 младшего разряда. Новое Z' корректируется, при этом к те­традам, из которых возникал перенос при получении (X + Уобр6 + 1), прибавляется 10, а к остальным не прибавляется.

Выполнение сложения и вычитания чисел со знаками сво­дится к выполнению сложения или вычитания модулей путем определения фактической выполняемой операции по знакам опе­рандов и виду выполняемой операции. Знак результата опреде­ляется отдельно. Например, при X < 0 и Y < 0 вычитание X- Y заменяется вычитанием | Y | - | X |. Затем знак результата меняется на противоположный знаку (| Y | - | X |).

Двоично-десятичное умножение сводится к образованию и многократному сложению частичных двоично-десятичных произведений. Умножение двоично-десятичных чисел выпол­няется следующим образом:

1) сумма частичных произведений полагается равной нулю;

2) анализируется очередная цифра (тетрада) множителя, и множимое прибавляется к сумме частичных произведений столько раз, какова цифра множителя;

3) сумма частичных произведений сдвигается вправо на 1 тетраду, и повторяются действия, указанные в п. 2, пока все цифры множителя не будут обработаны.

Для ускорения умножения часто отдельно формируются кратные множимого 8Х, 4Х, 2Х и IX, при наличии которых уменьшается число сложений при выполнении п. 2.

Двоично-десятичное деление выполняется путем много­кратных вычитаний, подобно тому, как это делается при обыч­ном делении.

Операции над числами с плавающей запятой

Арифметические операции над числами с плавающей запя­той более сложны, чем операции над числами с фиксированной запятой. Алгоритм сложения и вычитания чисел с плавающей запятой выглядит следующим образом:

Производится выравнивание порядков чисел. Порядок меньшего (по модулю) числа принимается равным порядку большего, а мантисса меньшего числа сдвигается вправо на число разрядов, равное разности порядков чисел.

Производится сложение (вычитание) мантисс, в результа­те чего получается мантисса суммы (разности).

Порядок результата принимается равным порядку большего числа.

Полученная сумма (разность) нормализуется.
Выравнивание порядков начинается с их сравнения. Мантисса числа с меньшим порядком при выравнивании сдвигается впра­во на число разрядов, равное разности порядков.

Сложение (вычитание) мантисс производится по правилам сложения (вычитания) чисел с фиксированной запятой.

При умножении чисел с плавающей запятой порядки сомножителей складываются, а мантиссы перемножаются. Произведение нормализуется, и ему присваивается знак плюс, если сомножители имеют одинаковые знаки, и знак минус, если знаки разные.

Если мантисса множимого или множителя равна 0, то про­изведению можно присвоить значение 0 без выполнения умно­жения мантисс. Если при суммировании порядков возникло переполнение и порядок отрицательный, то это означает, что произведение меньше минимального представляемого в маши­не числа, и в качестве результата операции может быть записан 0 без перемножения мантисс.

Если при суммировании порядков возникает переполнение и порядок положительный, может оказаться, что результат все-таки находится в диапазоне чисел, представляемых в машине, так как при умножении мантисс возможно нарушение норма­лизации вправо, и после нормализации мантиссы переполнение в порядке может исчезнуть.

При делении чисел с плавающей запятой мантисса частного равна частному от деления мантиссы делимого на мантиссу де­лителя, а порядок частного - разности порядков делимого и делителя. Частное нормализуется, и ему присваивается знак плюс, если делимое и делитель имеют одинаковые знаки, и знак минус, если разные.

Если делимое равно 0, то в частное может быть записан 0 без выполнения деления. Если при вычитании порядков обра­зовалось переполнение с положительным знаком или если де­литель равен 0, то деление не производится и формируется сиг­нал прерывания.

При делении нормализованных чисел с плавающей запятой может оказаться, что мантисса делимого больше мантиссы де­лителя, и мантисса частного образуется с переполнением. Для устранения этого явления перед делением мантисс нарушают нормализацию делителя сдвигом на разряд влево. Тогда нару­шения нормализации частного влево не возникает.

 

Устройства управления

Классификация УУ

Устройство управления (УУ) управляет работой процессора, обеспечивая автоматическое выполнение команд программы. Выполнение команды процессором представляет собой последовательность следующих действий (иногда называемых машинными циклами):

-выборка команды из памяти и ее декодирование (дешифрация кода операции);

-формирование адреса следующей команды;

-формирование исполнительного адреса операнда и выборка его из памяти;

-исполнение операции и запись результата в память.

Для выполнения каждого машинного цикла необходим ряд управляющих сигналов, формируемых устройством управления.

В зависимости от способа формирования управляющих сигналов различают два основных типа УУ:

- аппаратные (с жесткой или схемной логикой);

- микропрограммные (с хранимой в памяти логикой).

В аппаратных УУ для каждой операции, задаваемой кодом операции команды, строится набор схем, которые в нужных тактах формируют соответствующие управляющие сигналы.

В УУ с микропрограммным управлением каждой операции соответствует набор микрокоманд, хранимых в памяти микрокоманд. Каждая микрокоманда несет информацию о микрооперациях, подлежащих выполнению в течение машинного такта и указания, какая микрокоманда должна быть выбрана из памяти следующей. Последовательность микрокоманд, выполняющая одну машинную команду или некоторую процедуру, образует микропрограмму.

 

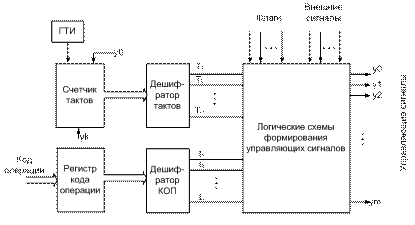
Аппаратные УУ

Управляющие устройства с жесткой логикой представляют собой логические схемы, вырабатывающие распределенные во времени управляющие сигналы. В отличие от управляющих устройств с хранимой в памяти логикой в аппаратных УУ нельзя изменить логику работы без изменения их схемы. Типичная структурная схема управляющего автомата с жесткой логикой показана на рисунке 4.9. Данный УА можно рассматривать в качестве автомата с конечным числом состояний (конечный автомат), который на каждом такте переходит из одного

Рисунок 4.9 - Схема блока формирования сигналов управления

 

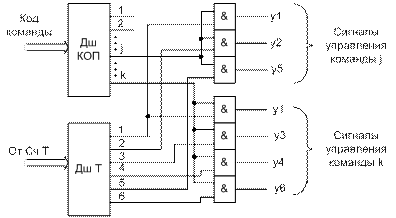
состояния в другое, определяемое содержи­мым регистра команды, кодами условий и внешними сигналами. Выходами такого автомата являются управляющие сигналы. Формируемая им последовательность операций задается физическими связями между логическими элементами.

В состав схемы входят регистр кода операции, являющейся частью регистра команд процессора, счетчик тактов, дешифратор тактов и дешифратор кода операции (Дешифратор КОП), а также логические схемы формирования управляющих сигналов. На счетчик тактов поступают сигналы от генератора тактовых импульсов (ГТИ). Состояние счетчика представляют собой номера тактов, изменяющие от 1 до m. Дешифратор тактов формирует на i-м выходе единичный сигнал при i-м состоянии счетчика тактов, т.е. во время i-го такта.

Принцип построения логических схем формирования управляющих сигналов поясняется на рисунке 4.10. На нем изображен фрагмент схемы, обеспечивающий выработку управляющих сигналов y1_, y2 и y3 выполнения команды сложения на тактах T₁,T₂, T₆.

В общем случае значения управляющих сигналов зависят еще от оповещающих сигналов U={u₁, u₂… u_n}, отражающих ход вычислительного процесса. Для реализации этих зависимостей логические элементы, представленные на рисунке 4.10, берутся многовходовыми и на них подаются требуемые сигналы логических условий.

 

 

Рисунок 4.10 - Фрагмент логической схемы формирования управляющих сигналов

 

Сигналы y0 и yk (см. рисунок 4.9) обычно используются для определения моментов начала и окончания выполнения команд. С этой целью они используются для управления работой счетчика тактов. Управ­ляющий сигнал y0 (Пуск) указывает на начало выполнения команды. Когда он установлен в 1, в конце каждого такто­вого цикла значение счетчика увеличивается на 1. Если же его значение становится рав­ным 0, отсчет шагов прекращается. Сигнал yk (Останов) сбрасывает счетчик тактов в начальное состояние, обеспечивая начало нового цикла выборки команды.

Серьезным недостатком рассмотренных схем является одинаковое число тактов, необходимых для выполнения всех команд, значение которого выбирается по наиболее длинной команде. Это приводит к непроизводительным затратам времени и, как следствие, к уменьшению быстродействия процессора. Для устранения этого недостатка применяют УУ с переменным числом тактов, в котором используют счетчик тактов с изменяемым модулем счета. Для коротких команд используют счетчик с небольшим модулем счета и наоборот.

При реализации простой системы команд узлы устройства управления с жесткой логикой экономичны и позволяют обеспечить наибольшее быстродействие среди всех возможных методов построения УУ. Однако с возрастанием сложности системы команд усложнялись и схемы автоматов с жесткой логикой, при этом их быстродействие уменьшалось.

 

Микропрограммные УУ

Альтернативой аппаратного способа реализации УУ является микро­программное управление, согласно которому сигналы генерируются под управлением программы, подобной программе, написанной на машинном языке для ЭВМ. Этотпринципиально иной подход был предложен английским ученым М. Уилксом в начале 50-х годов. Его называют принципом микропрограммного управления. Он позволяет преодолеть сложности реализации УУ с жесткой логикой. В основу принципа микропрограммного управления заложен тот факт, что каждой машинной команде соответствует уникаль­ный код, называемый микрокомандой. Последовательность микрокоманд, реализующих машинную команду, образует микропрограмму. Микропрограммы размещаются в специальной управляющей памяти, называемой памятью микропрограмм. Выполнение любой команды в процессоре реализуется путем последовательного извлечения микрокоманд из памяти микропрограмм с последующей их дешифрацией для формирования управляющих сигналов, необходимых при выполнении конкретной команды.

Идея заинтересовала многих конструкторов ЭВМ, но на момент возникновения она была нереализуема, поскольку требовала использования быстрой памяти относительно большой емкости. Вернулись к ней в 1964 году, в ходе создания системы 360 фирмой IBM. С этого времени устройства управления с программируемой логикой стали чрезвычайно популярными и были встроены во многие компьютеры.

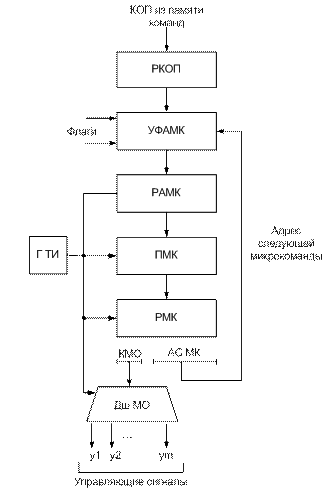
Структура блока микропрограммного управления (БМУ) с принудительной адресацией микрокоманд (МК) приведена на рис. 4.11. В состав БМУ входят память микрокоманд (ПМК), регистр адреса микрокоманд (РАМК), регистр микрокоманд (РМК), дешифратор микроопераций (ДшМО), генератор тактовых импульсов (ГТИ).

Код операции (КОП) поступает из ОП системы на регистр кода операции (РКОП), который задает начальный адрес микропрограммы. Адрес микропрограммы формируется устройством формирования адреса МК (УФАМК) и хранится в РАМК. По этому адресу из памяти микрокоманд (ПМК) БМУ считывается микрокоманда и фиксируется в регистре МК (РМК).

Микрокоманда содержит два основных поля: код микрооперации (КМО) и адрес следующей МК (АСМК)

КМО дешифрируется и преобразуется в набор сигналов y₁…y_m, управляющих функционированием процессора. Поле адреса следующей микрокоманды заносится в УФАМК, в результате чего производится выборка следующей МК.

 

 

Рисунок 4.11- Структура БМУ с принудительной адресацией МК

 

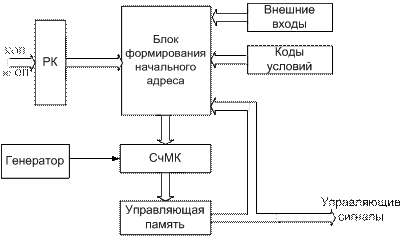
Структурная схема БМУ, использующего естественную адресацию микрокоманд, показана на рис. 4.12. Последовательное чтение слов из управляющей памяти обеспечивается счетчиком микропрограмм (СчМК). При каждой загрузке в регистр команд (РК) новой машинной команды в счётчик загружается выходное значение из блока формирования начального адреса. После этого на очередном такте производится автоматическое приращение содержимого СчМК для выбора из управ­ляющей памяти очередной команды. Благодаря этому управляющие сигналы по­ступают в разные части процессора в необходимой, для выполнения конкретной команды, последовательности и в нужные моменты времени.

Для поддержки ветвления в микропрограммах блок формирования начального адреса имеет входы, на которые заводятся коды условий (флаги) из регистра признаков и внешние сигналы, например, сигналы прерываний. Необходимые проверки кодов условий выполняются с по­мощью микрокоманд условного перехода.

Рисунок 4.12 - Структура БМУ с естественной адресацией МК

 

На формирователь начального адреса в этом случае возлагает­ся дополнительная функция - генерирование адреса перехода. По указанию мик­рокоманды этот блок загружает в счетчик СчМК новый адрес. Для поддержки услов­ных переходов на входы данного блока подаются не только КОП команды с РК, но и сигналы с внешних входов, а также коды условий.

В БМУ с естественной адресацией МК после выборки очередной микрокоманды из управляющей памяти происходит приращение значе­ния СчМК. Естественный порядок выборки МК нарушается в следующих случаях:

- если в РК загружается новая команда, в счетчик СчМК загружается начальный адрес ее микропрограммы;

- когда в последовательности выбираемых МК встречается микрокоманда перехода и условие пере­хода выполняется, в СчМК загружается адрес перехода;

- в случае появления микрокоманды “Останов” в СчМК загружается адрес микропрограммы для последующего выполнения очередной машинной команды.

БМУ с принудительной адресацией используются чаще, чем БМУ с естественной адресацией. Их общим достоинством является то, что замена одной системы команд на другую производится путем установки памяти микропрограмм с новой прошивкой. Кроме того, легко осуществляется эмуляция системы команд любого серийно выпускаемого процессора, что особенно важно при разработке контроллеров и специализированных ЭВМ. В этом случае можно использовать наработанное системное программное обеспечение серийной машины для отладки программ новой ЭВМ. Кроме того, микропрограммное управление позволяет легко создавать проблемно ориентированную систему команд в терминах управляемого объекта. Например, система команд для управления роботом - манипулятором может состоять из следующих команд: “Вправо”, “Влево”, “Поднять”, “Опустить”, и т.д. При использовании таких команд процесс написания программ для специализированной ЭВМ становится простым и может производиться оператором робота - манипулятора.