Как появились меры длины. Как измеряли на Руси

– Нельзя представить себе жизнь человека, не производящего измерений: это и портные, и механики, и обыкновенные школьники. Сегодня мы все знакомы с линейкой, метром. А что же существовало до того, как все это изобрели? Первыми измерительными приборами были части тела: пальцы рук, ладонь, ступня. Так, у древних египтян основной мерой длины служил локоть (расстояние от конца пальцев до согнутого локтя). Он делился на семь ладоней, а ладонь на четыре пальца.

(Учитель показывает, как измеряют локтем длину ленты, а затем предлагает проделать это двум-трем ученикам. Количество локтей получилось разное.)

– Чтобы измерения были более точными и не зависели от роста людей, в Древнем Египте придумали образцовые меры: локоть, ладонь, палец. Теперь было уже неважно, какой длины локоть или ладонь у человека, он измерял не своим, а общим локтем, т. е. условной палочкой. В Англии также существовали единицы длины, связанные с частями тела человека: дюйм (2,54 см) в переводе с голландского означает «большой палец»; фут (30 см 48 мм, или 12 дюймов) в переводе с английского – «нога»; ярд – это расстояние от носа короля Генриха I до конца среднего пальца его вытянутой руки.

Многие народы измеряли длину шагами, двойными шагами, тростями. Очень большие расстояния измерялись переходами, привалами или даже днями.

В Японии существовала мера, называемая лошадиным башмаком. Она была равна пути, в течение которого изнашивалась соломенная подошва, привязанная к копытам лошади.

У многих народов расстояние определялось длительностью полета стрелы или пушечного ядра. До сегодняшнего дня сохранилось выражение «не подпустить на пушечный выстрел».

– А кто знает, какие меры длины использовали издавна на Руси? (Сажень (маховая, косая), верста, локоть, аршин.) О локте мы уже говорили. Маховая сажень (1,76 м) – расстояние между раскинутыми в стороны руками. Косая сажень (2,48 м) – расстояние от каблука правой ноги до кончиков пальцев вытянутой вверх левой руки. Слово аршин пришло с Востока. Приезжие купцы торговали невиданными тканями: китайским шелком, индийской парчой, бархатом, которые отмеряли аршинами (с персидского – «локоть»). Он равен 71 см.

Учитель может предложить следующие вопросы-задания:

1. Измерить длину парты в локтях, ладонях.

2. Какого роста была Дюймовочка?

3. Каков был рост человека, про которого говорят «от горшка два вершка»?

4. 7 футов под килем – это сколько метров?

Для выполнения этого задания удобно пользоваться следующей таблицей:

Сажень = 3 аршина = 7 футов = 2 м 13 см Фут = 12 дюймов = 30 см 48 мм Аршин = 71 см Вершок = 4 см 45 мм Дюйм = 2 см 54 мм

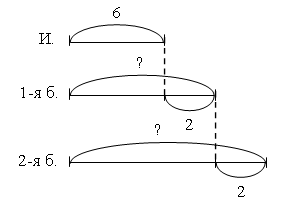
Задание № 18 (с. 35).

– Прочитайте старинную задачу.

– Что вам известно? Что требуется узнать?

– Какую новую единицу длины содержит эта задача? (Аршин.)

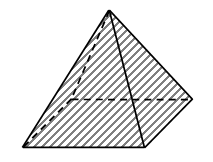
I способ:

1) 6 + 2 = 8 (аршин) – высота 1-й березы.

2) 8 + 2 = 10 (аршин) – высота 2-й березы.

II способ:

1) 2 + 2 = 4 (аршина) – выше 2-я береза, чем изба.

2) 6 + 4 = 10 (аршин) – высота 2-й березы.

Ответ: 10 аршин.

3. Фронтальная работа.

– Рассмотрите чертеж. Как называется данное геометрическое тело? (Пирамида.)

Учитель демонстрирует модель пирамиды.

– Сравните данную модель пирамиды с ее чертежом в тетради.

– Сколько всего граней у пирамиды? (Пять.)

– Сколько граней вы видите на модели? (Две.)

– Какие это грани? (Боковые.)

– Сколько невидимых граней на модели? (Три.)

– Какие это грани? (Две боковые грани и одна нижняя, т. е. основание.)

– Сколько граней нужно раскрасить на чертеже? (Три.)

После этого учитель предлагает раскрасить невидимые грани пирамиды на чертеже. (Раскрашенным окажется весь чертеж.)

4. Работа в печатной тетради № 1.

Задание № 47.

– Какие числа ввели в «машину»?

Учащиеся. В «машину» ввели неизвестное число. Машина прибавила к нему 7. Вышло из «машины» число 13. К неизвестному числу стрелка не идет. Изображаем «машину», обратную данной: –7.

Идем по стрелке: 13 – 7. Выполняем вычисление.

Получаем 6. Значит, неизвестное число 6. Записываем его в «окошко».

Выполняем проверку. Идем по верхней стрелке: 6 + 7 = 13 (верно).

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите старинные русские единицы длины.

– Назовите признаки пирамиды.

Домашнее задание: № 14, 16 (учебник); № 46, 49, 51 (рабочая тетрадь).

Урок 15
Многоугольник и его элементы

Цели урока: ввести понятие «многоугольник»; научить находить и показывать вершины, стороны и углы многоугольника; рассмотреть обозначение многоугольника латинскими буквами; совершенствовать навыки решения задач; развивать внимание и пространственное мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Имя какого сказочного героя здесь зашифровано?

15 – 7 + 4	А		16 – 10 + 8	О
12 – 6 + 2	Д		6 + 5 + 0	Е
9 + 9 – 1	Р		9 + 5 – 7	Г

 

Г	Е	Р	Д	А

2. Нарисуйте недостающую фигуру, чтобы в каждом ряду были фигуры разной формы.

3. Сравните тексты задач. Чем они похожи? Чем отличаются?

На одной остановке из автобуса вышли 10 человек, на другой – 20. На сколько меньше пассажиров стало в автобусе?

На одной остановке из автобуса вышли 10 человек, на другой – 20. Сколько человек вышло из автобуса?

– Можно ли утверждать, что решения этих задач одинаковы?

III. Сообщение темы урока.

– Рассмотрите чертежи на доске:

– Какую закономерность вы обнаружили? (У каждой следующей фигуры увеличивается количество углов и сторон на 1.)

– Название каких фигур вы знаете?

– Какие затруднения у вас возникли?

– Как можно назвать все эти фигуры одним словом?

– Об этом мы и будем говорить сегодня на уроке.