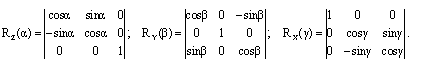Заполнение области в компьютерной графике

Задача заключается в закрашивании произвольного контура, нарисованного в растре. Задается область, ограниченная набором пикселей заданного цвета, и точка (x,y), лежащая внутри этой области.

Простейший алгоритм заполнения заключается в следующем. Цвет текущего пикселя изменяется на нужный цвет заполнения. Затем проводится анализ цветов всех соседних пикселей. Если цвет некоторого соседнего пикселя не равен цвету границы контура или цвету заполнения, то цвет этого пикселя изменяется на цвет заполнения. Затем анализируется цвет пикселей, соседних с предыдущими. И так далее до тех пор, пока внутри контура все пиксели не перекрасятся в цвет заполнения.

 

Алгоритм закрашивания линиями отличается тем, что на каждом шаге закрашивания рисуется горизонтальная линия, которая размещается между пикселями контура.

 

Волновой алгоритм закрашивания основан на поиске трассы на графе. Здесь для начальной точки (вершины на графе) находятся соседние точки (другие вершины), которые отвечают двум условиям: эти вершины связаны с начальной и они рассматриваются впервые. Соседние вершины текущей итерации становятся текущими точками для поиска новых соседних вершин в следующей итерации. По достижении конечной точки (границы области) совершается обратный цикл к начальной точке, в ходе которого находятся все кратчайшие пути между двумя заданными точками на графе и определяется порядок закраски пикселей.

 

13. Понятие двумерных геометрических преобразований

Геометрические преобразования – такие преобразования графического объекта, которые не нарушают структуру изображения, то есть если некоторая точка a(x,y) принадлежит линии А, то преобразованная точка a’(x’,y’) принадлежит преобразованной линии А’; А принадлежит поверхности A и А’ принадлежит поверхности A’ после выполнения преобразования. Изображение может двигаться, наклоняться, расширяться, но структура изображения не должна теряться. Поэтому тип примитива не влияет на выполнение геометрических преобразований.

Существует всего три типа двухмерных геометрических преобразований:1. Поворот.2. Перенос.3. Масштабирование.

 

14. 2D геометрические преобразования. Поворот

Из геометрических соображений получаем (рис. 18):

x’ = x·cos a + y·sin a;

y’ = - x·sin a + y·cos a.

Если выполним поворот изображения, заданного в системе координат XOY, получим координаты точек этого изображения в системеX’OY’. Повернем затем систему X’OY’ назад в первоначальное положение.

При замене a на –a получим поворот в другую сторону.

Кроме того, этот поворот в плоскости XOY можно представить как частный случай поворота в пространстве XYZ, а именно как плоский поворот относительно оси Z на угол a в трехмерном пространстве XYZ:

x’= x·Сos a + y·Sin a + z·0

y’= - x·Sin a + y·cos a + z·0

z’= x·0 + y·0 + z·1.

То же в матричном виде:

[x’ y’ z’] = [x y z]

Аналогично получается соотношение для новых координат точки, полученных в результате ее поворота относительно оси Y на угол b:

x’=x·cos b + y·0 - z·sin b

y’=x·0 + y·1 + z·0

z’= x·sin b + y·0 + z·cos b.

Поворот вокруг оси Х на угол g:

x’= x·1 + y·0 + z·0

y’= x·0 + y·cos g + z·sin g

z’= x·0 – y·sin g + z·cos g.

Соответствующие матрицы поворотов имеют вид (рис. 19):

 

 

15. 2D геометрические преобразования. Перенос

Перенос точки производится добавлением к каждой координате точки положительной или отрицательной константы. Если обозначить параметры переноса через Т_х (перенос в направлении оси х), Т_у (перенос в направлении оси у), T_z (перенос в направлении оси z), получим координаты перенесенной точки Р(x,y,z):

P’(x’,y’,z’) = Р(x,y,z) + T(Т_х,Т_у,T_z) или (x’,y’,z’) = (x,y,z) + (Т_х,Т_у,T_z).

Можно сюда добавить операцию поворота:

P’(x’,y’,z’) = Р(x,y,z) · R(x,y,z)+ T(Т_х,Т_у,T_z).

 

16. 2D геометрические преобразования. Масштабирование

 

Операция масштабирования заключается в том, что каждая координата точки умножается на некоторую величину. Преобразование выполняется с помощью матрицы масштабирования S: P’= P·S, или

где S_x,S_y,S_z – коэффициенты масштабирования, являющиеся масштабными множителями соответственно в х-, у-, z- направлениях. Если масштабные множители меньше единицы, то преобразуемый объект сжимается, если они больше единицы, то объект растягивается. Если S_x= S_y = S_z = C, объект сжимается или растягивается одинаково по всем направлениям, что соответствует операции общего масштабирования. При общем масштабировании (равномерно по всем осям без изменения формы объекта) матрицу S можно заменить скаляром C:

(x’,y’,z’) = С· (x,y,z), где С=const.

Можно объединить все три преобразования в общую формулу:

P’ = S · R · P + T,

где P – исходная точка; P’ – преобразованная точка; S, R, T – соответствующие матрицы.

 

17. 2D геометрические преобразования. Матричные уравнения

 

Решение геометрических задач в однородной системе координат становится проще и эффективнее, чем в неоднородных, хотя размерность задачи возрастает на единицу. Это происходит потому, что в однородных координатах выполнение всех геометрических преобразований сводится к одной операции – перемножению двух квадратных матриц 3x3 или матрицы 3x3 и вектора размерностью 3.

В однородных координатах вектор точки Р и матрицы поворота R, переноса T и масштабирования S принимают вид

 

18. 2D геометрические преобразования. Общий алгоритм

1. Определение графического объекта (исходные координаты всех базовых точек).

2. Определение констант геометрических преобразований (a, T_x, T_y, S_x, S_y);

3. Вычисление матриц геометрических преобразований S, R, T (вызов функций Tran2, Rot2, Scale2).

4. Вычисление общей матрицы всех геометрических преобразований: M = R·T; Q = S·M (применяем функцию Mult2).

5. Вычисление необходимых дополнительных точек графического объекта по базовым (точки на дуге по центру и радиусу и др.).

6. Вычисление новых координат всех необходимых точек: P’ = Q·P, где P = (х, у, 1) – исходная точка; P’ = (х’, у’, 1) – полученная в результате преобразования.

7. Визуализация точек P’ и построение отрезков, соединяющих предыдущую построенную точку с последующей (текущей).

Шаги 5, 6, 7 повторяются для всех точек объекта.

 

19. Преобразование области. Задача кадрирования

Кадрирование точек выполняется просто. Необходимо лишь проверить условие |ix| + |iy| = 0. Если точка находится внутри экранной области, она изображается, в противном случае – отбрасывается.

Кадрирование отрезков – более сложная задача. Здесь различается несколько случаев, определяемых тем, какая часть (или какие части) отрезка выходят за пределы графического окна.

При выполнении операции кадрирования решаются две задачи – отсечения и покрытия.