
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многоразрядные параллельные сумматорыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Параллельные многоразрядные сумматоры строятся на основе ПОС. На рис. 15.8 приведена схема параллельного n-разрядного сумматора с последовательным переносом, составленного из одноразрядных сумматоров. Правильные значения
частичных сумм S0 … Sn-1 будут устанавливаться последовательно, начиная с младшего разряда. Самым последним устанавливается правильное значение частичной суммы Sn-1. Максимальное время суммирования в таком сумматоре составляет:
Примером интегрального параллельного сумматора с последовательным переносом является микросхема К564ИМ1. Это - четырёхразрядный сумматор, выполненный по КМДП-технологии. Его структурная схема и УГО показаны соответственно на рис.15.9,а и 15.9,б. Он отличается от схемы рис.15.8 наличием схемы ускоренного формирования выходного переноса c4 (подробно такая схема рассмотрена в п.15.1.4), подаваемого на вход переноса следующей микросхемы при наращивании разрядности. Благодаря наличию такой схемы удаётся увеличить быстродействие многоразрядных параллельных сумматоров с последовательным переносом. При напряжении источника питания Uп =10 В время задержки по трактам от входа c0 до выхода переноса c4 и от входов слагаемых младших разрядов до выхода суммы старшего разряда составляет 140 нc. При Uп = 5 В задержка сигналов увеличивается до 300 нc.
Недостатком параллельных многоразрядных сумматоров с последовательным переносом является их сравнительно низкое быстродействие, связанное с большим временем суммирования. Увеличение быстродействия сумматоров можно осуществить по двум направлениям: 1) уменьшением параметров tas, tap, tps, tpp и объема оборудования, оцениваемого числом входов используемых ЛЭ; 2) уменьшением времени суммирования tсум. Первое направление представляет собой классическую задачу синтеза сумматора, не решенную окончательно до настоящего времени. За время существования ЭВМ эта задача решалась эмпирически и были получены удачные решения. В настоящее время широкое распространение получили сумматоры, построенные на основании уравнений (15.5) и (15.8), представляющих самодвойственные функции. Второе направление связано с уменьшением (или даже исключением) влияния разрядности суммируемых чисел на tcyм путем одновременного формирования переносов во все разряды. Такие сумматоры называют параллельными с параллельным переносом. Для синтеза таких сумматоров представим выражение (15.5) для переноса в старший разряд в виде:
или где Сигнал gi = 1 вырабатывается тогда, когда a i = b i =1 и не зависит от значения переноса c i в данный разряд. Поэтому функцию gi = a i b i называют функцией генерации переноса. Сигнал pi = a i Для четырехразрядного сумматора функции генерации и распространения переноса будут иметь вид:
Тогда функции переноса для первого и последующего разрядов можно записать в виде:

Формулы (15.13) показывают, что переносы из каждого разряда можно выразить непосредственно через функции генерации gi и распространения переноса pi, определяемые только значениями слагаемых независимо от их положения в разрядной сетке, и перенос c0 в младший разряд. Можно показать также, что
Следовательно, одновременно (параллельно) с формированием сигналов переноса по сформированным значениям функций gi и pi можно формировать частичные суммы si (но небольшая задержка должна быть, чтобы успели выработаться сигналы переноса).
Структурная схема рассмотренного сумматора с параллельным поразрядным переносом приведена на рис. 15.10. Блок генерации и распространения совместно с блоком переноса образуют схему (блок) ускоренного переноса (сокращенно СУП или БУП). Для реализации этого сумматора в базисе И-НЕ необходимо преобразовать уравнения (15.12) следующим образом:
В уравнениях (15.14)...(15.17) множители, стоящие после знака
Схема четырехразрядного параллельного сумматора, построенная в соответствии с уравнениями (15.14)... (15.17), приведена на рис.15.11. На этом рисунке пунктирными линиями обведены участки, которые не используются при c0 = 0. Из рисунка видно, что быстродействие параллельного сумматора с параллельным переносом равно времени задержки трех схем И-НЕ, формирующих сигнал переноса, плюс время задержки ПОС. В зависимости от типа одноразрядного сумматора время суммирования при параллельном переносе составляет tсум = (5-6) tзд.ла.. С ростом разрядности сумматора увеличивается число входов конъ-юнкторов, используемых для формирования переносов в старшие разряды. Поэтому сумматоры с параллельным переносом реализуют лишь для малого числа разрядов (обычно для четырех). Однако принцип параллельного переноса используется в широко распространенных сумматорах с групповой структурой.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.87 (0.011 с.) |


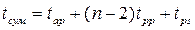 . (15.9)
. (15.9)


 (15.10)
(15.10)
 . (15.11)
. (15.11) b i = 1 разрешает прохождение переноса на выход сумматора, когда a i либо b i равно нулю и называется функцией распространения переноса.
b i = 1 разрешает прохождение переноса на выход сумматора, когда a i либо b i равно нулю и называется функцией распространения переноса.
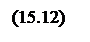
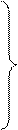 c1 = g0
c1 = g0 
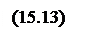
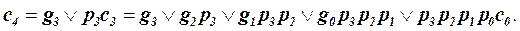
 . Действительно:
. Действительно:




 Поступая аналогичным образом, получим:
Поступая аналогичным образом, получим:

 (конъюнкции), присутствуют только в том случае, если c0 =1.
(конъюнкции), присутствуют только в том случае, если c0 =1.



