
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Другие области применения мультиплексоровСодержание книги
Поиск на нашем сайте
Уравнение (14.4) для мультиплексора 4-1 без учета разрешающего сигнала
В этом уравнении переменные Функции трех переменных F = f (x 1, х 2, х 3) соответствует карта Карно из восьми ячеек (рис. 14.10,а). Если на управляющие входы подать переменные х1, х2, то на информационные входы возможно поступление сигналов D0, D1 D2 и D3 определяемых значениями третьей переменной х3. При этом когда х1 =0 и х2 =0, то две верхние ячейки соответствуют значению D0. Значению D1 соответствуют две ячейки, у которых х 1=1 и х 2=0, ячейки, для которых х 1=0 и х 2=1 определяют значение D2, а ячейки, для которых х 1=1 и х 2=1- значение D3 (рис. 14.10,б). Таким образом, восьмиячеечная карта Карно для трех переменных оказалась разделенной на четыре двухъячеечные карты Карно для одной переменной, и каждой паре ячеек ставится в соответствие информационный вход.
Вместо переменных х 1 и х 2на управляющие входы мультиплексора можно подавать переменные x 1и х 3 либо х 2 и х 3. При подаче на управляющие входы переменных х 1 и х 3значения сигналов D0...D3 определятся парами ячеек, показанными на рис. 14.10,в. Если на управляющие входы подать переменные х 2 и х 3, то пары ячеек, определяющих сигналы D0...D3, определятся так, как показано на рис. 14.10,г. В качестве примера рассмотрим реализацию на мультиплексоре 4–1 функцию трех переменных Если в качестве управляющих переменных выбрать х 1 и х 3, то информационные сигналы D 0... D 3 будут определяться парами ячеек, показанными на рис. 14.10,в, минимизация которых дает: D 0 = x 2, D 1 = l, D 2 = 0, D 3 = x 2, а если бы управляющими переменными были x 2 и х 3,то в соответствии с рис. 14.10,г информационные сигналы имели бы следующий вид: D 0=0, D 1= Сумматоры Сумматором называют операционный узел ЭВМ, выполняющий операцию сложения двух чисел, представленных в двоичном коде. Известно, что все многообразие математических операций (сложение, вычитание, деление, возведение в степень, вычисление тригонометрических функций и т.п.) можно получить с помощью операций сложения прямых и обратных кодов чисел, сдвинутых влево или вправо на то или иное число разрядов. Поэтому скорость выполнения вычислительных процессов в ЭВМ существенно зависит от быстродействия сумматоров. По принятой в ЭВМ системе счисления и кодирования сумматоры подразделяются на двоичные, десятичные, двоично-десятичные и др. По способу организации суммирования чисел сумматоры могут быть комбинационными и накапливающими. В комбинационных сумматорах результат суммирования не запоминается. В накапливающих сумматорах, имеющих память, после добавления к содержимому сумматора очередного слагаемого происходит запоминание полученного результата. По способу организации межразрядных переносов сумматоры делятся на параллельные, последовательные и c групповой структурой. В параллельных сумматорах суммирование одноименных разрядов чисел осуществляется одновременно (параллельно), а в последовательных — последовательно от младших к старшим. В сумматорах с групповой структурой суммируемые числа разбиваются на группы, построенные как параллельные сумматоры, а полученные в группах переносы складываются затем последовательно (параллельно-последовательные сумматоры) или параллельно. В последнем случае сумматоры называют параллельными с параллельно-параллельным переносом. По способу тактирования различают синхронные и асинхронные сумматоры. В синхронных сумматорах для выполнения процесса суммирования отводится постоянное время независимо от разрядности суммируемых чисел, а в асинхронных после завершения процесса суммирования вырабатывается специальный сигнал (признак). Поэтому у асинхронных сумматоров среднее время суммирования меньше, чем у синхронных.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.144.139 (0.006 с.) |

 При выполнении различных математических операций часто возникает необходимость сдвига кода числа вправо (в сторону младших разрядов) или влево (в сторону старших разрядов) на один или несколько разрядов. На рис.14.12 показан один, i -й разряд параллельного сдвигателя. В полной схеме сдвигателя ко входу каждого разряда регистра RG2 подключено по такому же мультиплексору, входы данных которого в свою очередь подключены к выходам нескольких разрядов регистра RG1. На адресные (управляющие) входы мультиплексоров всех разрядов подается один и тот же код А1А0, в зависимости от которого в i -й разряд RG2 будет переписываться содержимое различных разрядов RG1. При А1А0=01 данные регистры RG1 будут передаваться в одноименные разряды RG2 без сдвига. При коде А1А0=00 в i -й разряд регистра RG2 поступит содержимое соседнего младшего, (i -1)- разряда регистра RG1, т.е. передача информации произойдет со сдвигом на один разряд влево. При кодах А1А0=10 и А1А0=11 передача информации из регистра RG1 в регистр RG2 будет происходить со сдвигом справо соответственно на один или два разряда. Применяя мультиплексор с большим числом входов (8 – 1, 16 – 1), подключаемых к соответствующим разрядам регистра-передатчика, можно строить сдвигатели, способные очень быстро (за время, определяемое задержкой мультиплексора и регистра-приемника) сдвигать код числа в любую сторону на любое заданное число разрядов.
При выполнении различных математических операций часто возникает необходимость сдвига кода числа вправо (в сторону младших разрядов) или влево (в сторону старших разрядов) на один или несколько разрядов. На рис.14.12 показан один, i -й разряд параллельного сдвигателя. В полной схеме сдвигателя ко входу каждого разряда регистра RG2 подключено по такому же мультиплексору, входы данных которого в свою очередь подключены к выходам нескольких разрядов регистра RG1. На адресные (управляющие) входы мультиплексоров всех разрядов подается один и тот же код А1А0, в зависимости от которого в i -й разряд RG2 будет переписываться содержимое различных разрядов RG1. При А1А0=01 данные регистры RG1 будут передаваться в одноименные разряды RG2 без сдвига. При коде А1А0=00 в i -й разряд регистра RG2 поступит содержимое соседнего младшего, (i -1)- разряда регистра RG1, т.е. передача информации произойдет со сдвигом на один разряд влево. При кодах А1А0=10 и А1А0=11 передача информации из регистра RG1 в регистр RG2 будет происходить со сдвигом справо соответственно на один или два разряда. Применяя мультиплексор с большим числом входов (8 – 1, 16 – 1), подключаемых к соответствующим разрядам регистра-передатчика, можно строить сдвигатели, способные очень быстро (за время, определяемое задержкой мультиплексора и регистра-приемника) сдвигать код числа в любую сторону на любое заданное число разрядов. Мультиплексоры удобно применять в устройствах используемых для передачи информации с регистра или другого устройства прямым или обратным кодом в зависимости от значения управляющего сигнала. С этой целью каждый разряд регистра дополняется мультиплексором 2-1, к одному входу которого подключается прямой выход разряда регистра, а ко второму – инверсный. При отсутствии мультиплексора 2-1 в используемой серии его можно построить по рис.14.13. В этом случае при А=0 на выходе мультиплексора получается обратный код сигнала от i-го разряда, а при А=1 –прямой.
Мультиплексоры удобно применять в устройствах используемых для передачи информации с регистра или другого устройства прямым или обратным кодом в зависимости от значения управляющего сигнала. С этой целью каждый разряд регистра дополняется мультиплексором 2-1, к одному входу которого подключается прямой выход разряда регистра, а ко второму – инверсный. При отсутствии мультиплексора 2-1 в используемой серии его можно построить по рис.14.13. В этом случае при А=0 на выходе мультиплексора получается обратный код сигнала от i-го разряда, а при А=1 –прямой.
 имеет вид:
имеет вид:
 и
и  представляют собой сигналы на управляющих (адресных) входах. Всегда
представляют собой сигналы на управляющих (адресных) входах. Всегда  или 1. В общей сложности существует
или 1. В общей сложности существует  =256 возможных комбинаций четырех входных сигналов и мультиплексор «4-1» может сгенерировать любую из 256 возможных логических функций от трех переменных.
=256 возможных комбинаций четырех входных сигналов и мультиплексор «4-1» может сгенерировать любую из 256 возможных логических функций от трех переменных.
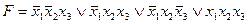 .Сначала эту функцию изображаем на карте Карно (рис. 14.11,а) и произвольно выбираем переменные, которые следует подать на управляющие входы мультиплексора. Пусть это будут переменные x 1 и х 2. Тогда сигналы D 0... D 3, подаваемые на информационные входы, будут определяться парами ячеек, показанными на рис. 14.10,б. Минимизируя набор из четырех функций одной переменной х 3, получим: D 0 = x3, D 1 = l, D 2 = 0, D 3 = x3. Реализация функции показана на рис. 14.11,б.
.Сначала эту функцию изображаем на карте Карно (рис. 14.11,а) и произвольно выбираем переменные, которые следует подать на управляющие входы мультиплексора. Пусть это будут переменные x 1 и х 2. Тогда сигналы D 0... D 3, подаваемые на информационные входы, будут определяться парами ячеек, показанными на рис. 14.10,б. Минимизируя набор из четырех функций одной переменной х 3, получим: D 0 = x3, D 1 = l, D 2 = 0, D 3 = x3. Реализация функции показана на рис. 14.11,б. , D 2=
, D 2= 


