
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы мезонной теории ядерных силСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Основываясь на свойствах ядерных сил, японский теоретик Юкава предложил теорию, которая объясняла, как удерживаются нуклоны внутри ядра. За основу теории была взята теория Дирака и подобно фотону, Юкава предложил существование тяжелой частицы, служащей посредником ядерного взаимодействия, т.о. роль π – мезона для ядерной физики была понята в результате теоретического рассуждения. В микромире соотношение Гейзенберга Процессы, идущие с нарушением энергии в течение времени называются виртуальными, а частицы, участвующие в этих процессах называются виртуальными частицами. Виртуальная частица, двигаясь даже со скоростью света, может пройти расстояние не больше чем Оказалось, что при данных оценках получается масса Таким образом, была оценена масса кванта ядерного поля в первом приближении. Отметим, что из-за допущения, что протон и нейтрон являются состояниями одной и той же частицы (нуклона), из обменного характера нуклонного взаимодействия вытекает следующая картина: между двумя нуклонами, находящимися на малых расстояниях происходит обмен π – мезоном, который является переносчиком ядерного взаимодействия
Согласно выше сказанному, виртуальными будем называть такие процессы, которые идут с нарушением энергетического баланса и поэтому неспособны отойти от источника на расстояние
ГЛАВА V. Радиоактивность В природе существует достаточно большое число радиоактивных изотов и все существующие радиационные изотопы, как оказывается, важно распределить в виде трех семейств: 1. Семейство урана: начинается с изотопа 2. Семейство актино – урана начинается с изотопа 3. Семейство тория: начинается с изотопа Анализ закономерности изменения массового числа приводит к некоторому соотношению
Оказалось, что такое семейство есть и оно состоит из изотопов, невстречающихся в природе, т.е. искусственно полученных изотопов- это семейство нептуния. На рисунке показана N-Z диаграмма атомных ядер. Черными точками показаны стабильные ядра. Область расположения стабильных ядер обычно называют долиной стабильности. С левой стороны от стабильных ядер находятся ядра, перегруженные протонами (протоноизбыточные ядра), справа – ядра, перегруженные нейтронами (нейтроноизбыточные ядра). Протоноизбыточные ядра являются радиоактивными и превращаются в стабильные в основном в результате Неограниченность и нестабильность изотопов показывает протонно-нейтронная диаграмма, которую можно представить следующим образом
Эта диаграмма показывает, что все стабильные изотопы распределены по биссектрисе. Все нестабильные группируются вокруг биссектрисы. Подробный анализ показывает, что слева сверху группируются β+ нестабильные ядра; слева снизу Закон радиоактивного распада имеет следующий вид λ– постоянная распада; N0–число ядер в момент времени t=0; Постоянная распада находится по формуле Т - период полураспада или время, за которое распадается половина ядер.
§1. α – распад Известно, что условием стабильности ядер является энергия связи. Когда энергия связи отрицательна, происходит самопроизвольный распад. Энергетическое условие возможности самопроизвольного α –распада записывается в виде:
При этом основная часть энергии уносится α – частицей: α – распад характеризуется периодом полураспада, длиной пробега и кинетической энергией. Перечислим основные особенности α – распада, установленные опытным путем. 1. В большинстве случаев α – частицы, вылетающие при распаде ядер данного элемента, имеют одинаковые энергии, т. е. являются моноэнергетическими. 2. Наблюдаются ядра испускающие несколько типов моноэнергетических α – частиц, тонкая структура. Например,
-4,68 МэВ (4%).
3. Энергия α – частиц всех известных ядер заключена от 4МэВ< 4. Наблюдается группа ядер, испускающих α – частиц с энергией 10,5 МэВ., такие α – частицы называют длиннопробежными. 5. Периоды полураспада α – радиоактивных ядер меняются в очень широких пределах 10-7 С < Т < 1015 лет. 6. В 1911 г. Гейгер и Нэттол нашли, что для а-радиоактивных элементов всех трех радиоактивных семейств существует зависимость между постоянной распада ядра Энергетическая схема α – распада объясняла все свойства α – распада, кроме закона Гейгера — Нэттола, который связывает постоянную распада ядра Если представить α – частицу в ядре некоторого радиуса Оценим коэффициент прозрачности. Впервые была применена в ядерной физике квантовая механика, для рассмотрения α – распада. В данном случае рассмотрим задачу для прямоугольного барьера. Краевые эффекты не учитываются. Если слева к барьеру подходит частица с энергией Е, которая Если представить частицу как волну, то
Отбросив временную часть, будем иметь в 1 области
В третьей области Эти оба выражения являются решением данного уравнения Шредингера
В области 2 уравнение Шредингера имеет вид:
Мы имеем 5 неизвестных и 4 уравнения. Т.к. коэффициент прозрач-ности равен
Где
Подставив
откуда
Аналогично можно получить другие коэффициенты, решая 3 и 4 уравнение
где
а
Тогда получим коэффициент прозрачности, Величина коэффициента прозрачности барьера представляет собой вероятность прохождения частицы сквозь потенциальный барьер. Полученная зависимость может быть представлена как Перечислим основные недостатки теории α – распада: 1. Отсутствие надежных методов вычисления предэкспоненциального множителя 2. В квантовой теории не вводится поправка на радиус самой α – частицы, следовательно, не учитывается вероятность образования самой α – частицы, т.к. считается, что она в самом ядре. Если учесть вероятность образования самой α – частицы внутри ядра, то это уменьшит общую вероятность; 3. Вероятность уменьшается еще больше, если учитывать роль момента количества движения, выносимого α – частицей, но этот эффект не значителен. §2. β – распад Явление радиоактивности было открыто в 1896 г. Беккерелем и через несколько лет стало ясно, что распадающиеся ядра испускают 3 типа излучения, названные согласно первым буквам греческого алфавита α, β, γ – излучение. Самым загадочным из них оказался β − распад. β − распад - это есть процесс превращения нестабильного ядра в ядро изобар, отличающегося по заряду на Известно три типа β− распада: 1. или
2.
3. При
Измерение энергии, вылетевшего электрона показало, что электроны имеют непрерывный спектр.
Таким образом, существует некоторая максимальная интенсивность, которая потом монотонно убывает и β − спектр каждого электрона имеет определенную величину β−распад – это процесс не внутриядерный, а внутринуклонный, т.е. он гораздо сложнее чем α
Основы теории Ферми Впервые количественную теорию β− распада постулировал в 1935 г. Э. Ферми. Исходное положение Ферми аналогично представлениям, положенным в основу квантовой электродинамики. Ферми, исходил из того, что электрон и нейтрино в ядре не содержатся, а возникают в момент распада, как кванты света. Это подтверждается наличием β+ – распада, т.к. в противном случае надо было допустить, что в ядре есть и 1. Действительно, заряд и масса β− частицы совпадают с такими же характеристиками электронов и атомов; 2. 3. Наличие 4. Справедливость принципа Паули. Итак, Ферми допустил существование связи между протоном и нейтроном с одной стороны и электронов и нейтрино с другой стороны. Если допустить, что состояние частицы можно описать плоскими волнами с количеством движения Вид матричного элемента в теории β −распада неизвестен, хотя возможно несколько видов записи. Например, для перехода от нейтрона в протон матричный элемент- это есть
В теории Ферми находят время жизни ядра относительно β − распада, которое как оказалось, связано с энергией β − распада:
β-
β+
1 ε0 ε
При Чтобы сравнить теорию Ферми с опытом представляются два подхода: 1. Сравнить кривую 2. Исходя из известных Из теории Ферми:
Отметим, что начальные и конечные состояния ядра удовлетворяют определенным условиям, связанным с выполнением закона сохранения момента количества движения и четности и называются правилами отбора для разрешенных переходов. Существуют два правила отбора: 1. правила Ферми 2. правила – Гамова-Теллера. Существует 5 вариантов теории: скалярный, векторный, тензорный, псевдовекторный, псевдоскалярный. Отметим, что каждый вариант имеет свои правила отбора для разрешенных переходов: скалярный, векторный подчиняются правилам Ферми; тензорный, псевдовекторный подчиняются правилам Гамова-Теллера, псевдоскалярный не описывается Важную роль в слабых взаимодействиях сыграло определение четности. Понятие четности на примере волновой функции, удовлетворяющей уравнению Шредингера, понимается следующим образом: правая система координат никаким смещением или поворотом не может быть переведена в левую систему. Этот переход возможен только при зеркальном отражении, т.е. при инверсии координат. При зеркальной симметрии волновая функция делится на 2 класса: четные и нечетные функции. Четные функции - это функции, не изменяющиеся при инверсии координат. Нечетные функции - это функции, изменяющие свой знак при замене местами координат: Закон сохранения четности, физики считают универсальным, как и закон сохранения энергии. Однако, последние измерения К - мезонов показали, что они ведут себя и как четные и как нечетные в разных схемах. Т.к. константа взаимодействия Итак, теория Ферми для β−распада продержалась 25 лет, и только в 1957 г. потребовалось внести некоторые исправления. Они были внесены Фейманом и Гелманом. Слабые взаимодействия во всем похожи на электромагнитные, поэтому по аналогии с виртуальными фотонами электромагнитного взаимодействия Ферми вводится в рассмотрение промежуточный бозон, который до сих пор не обнаружен. ГЛАВА VI. Ядерные реакции Виды ядерных реакций Ядерные реакции в лабораторных условиях выполняются путем бомбардировки ядер, содержащихся в реакциях, в процессе которого меняется структура ядра. В основном, они осуществляются для выяснения механизма взаимодействия нуклонов друг с другом и нуклонов с ядрами или для определения той или иной квантовой характеристики ядра. Число известных ядерных реакций более тысячи. Рассмотрим типы ядерных реакций, имеющих историческое значение. В общем виде ядерные реакции можно записать в следующем виде:
Столкновения, при которых меняется структура ядра, называются ядерными столкновениями, а реакцию при этом обозначают Рассмотрим типы реакций: I) Ядерные реакции под действием а-частиц. В значительном числе случаев реакции под действием а-частиц сводятся к образованию составного ядра, которое потом распадается. Этим они сходны с реакциями, идущими под действием нейтронов и протонов. Существующее же различие в зарядах сказывается лишь на проницаемости кулоновского потенциального барьера. Сечения ядерных реакций, обусловленных захватом а-частиц в области малых энергий, ничтожно малы и быстро возрастают с увеличением энергии. Под действием частиц идут преимущественно реакции типа Высота кулоновского барьера для реакций на тяжелых ядрах имеет порядок 25 МзВ. При энергиях а - частиц, превышающих это значение, реакции типа 1) Реакция
2) Реакция
Примером такой реакции может быть реакция на алюминии, которая позволила супругам Кюри обнаружить исскуственную радиоактивность
3) В 1932 г. Чедвиг открыл существование нейтрона в подобной реакции на бериллии:
Эта реакция и в настоящее время широко используется как простейший источник нейтронов, α-частицы, так же как протоны и дейтроны, могут вызвать возбуждение ядер путем кулоновского взаимодействия. В каждом таком случае возбужденное ядро избавляется, в конце концов, от избыточной энергии путем испускания
II) Ядерные реакции под действием протонов. Под действием протонов идут реакции 1) Реакции типа 2) Реакции типа 3) Реакции типа 4) Реакции типа 5) Реакции типа III) Реакции, идущие под действием дейтрона. Ядерные реакции под действием дейтронов имеют большое практическое значение. Выход этих реакций обычно гораздо больше выходов соответствующих реакций под действием других заряженных частиц. Кроме того, следствием малой величины энергии связи дейтрона является большая энергия возбуждения промежуточного ядра, и, как правило, реакции с поглощением дейтрона экзоэнергетические Особенности протекания реакций под действием дейтронов определяются тем, что дейтрон представляет собой слабосвязанное «рыхлое» ядро ( При этом идут реакции Такие реакции при высоких энергиях называются реакциями срыва, а при малых энергиях — процессом Оппенгеймера — Филипса (или процессом неполного проникновения дейтрона в ядра). В отличие от рассмотренного выше механизма протекания ядерной реакции с образованием промежуточного ядра в процессах 3-го типа дейтрон вообще не попадает в атомное ядро. Благодаря большим размерам дейтрона при его приближении к ядру нейтрон может проникнуть в ядро мишени, когда протон будет находиться еще довольно далеко от ядра. При этом произойдет развал дейтрона, а из-за кулоновского отталкивания протон не проникнет в ядро. Поэтому при малых энергиях реакция 1) Реакции типа 2) Реакции типа 3) Бомбардировка ядра дейтроном, приводящая, как обычно, к образованию составного ядра. При этом идет реакция | ||||||
|
| Поделиться: |

 истолковывается как возможность отклонения от закона сохранения энергии, при переходах и превращениях энергии
истолковывается как возможность отклонения от закона сохранения энергии, при переходах и превращениях энергии  в течении времени
в течении времени  . Отсюда
. Отсюда  , а
, а  , и
, и  .
. , которое определяется размером ядра
, которое определяется размером ядра 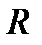 . Виртуальная частица не может пройти расстояние больше чем R от места своего рождения. Таким образом, если воспользоваться размерами ядра, то можно определить массу ядерного кванта
. Виртуальная частица не может пройти расстояние больше чем R от места своего рождения. Таким образом, если воспользоваться размерами ядра, то можно определить массу ядерного кванта 
 , что соответствует массе π – мезона.
, что соответствует массе π – мезона. ,
,  ,
, ,
, 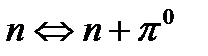 .Это следует понимать так. Часть времени нуклон находится в заряженном состоянии, а часть в виртуальном. Обмен виртуальными π – мезонами обусловлен взаимодействием между нуклонами.
.Это следует понимать так. Часть времени нуклон находится в заряженном состоянии, а часть в виртуальном. Обмен виртуальными π – мезонами обусловлен взаимодействием между нуклонами. . Для получения потенциала Юкава рассматривается поле ядерных сил по аналогии с электрическим взаимодействием. Взаимодействие между нуклонами включает в себя множество π– мезонов и должно включать в себя выводы, необходимые для решения задачи многих тел. Следовательно, ядерный потенциал не будет окончательно определен для области, где неупругие процессы играют существенную роль; кроме того, необходимо чтобы потенциал ядерного взаимодействия кроме обменного взаимодействия учитывал бы сильное отталкивание на малых расстояниях.
. Для получения потенциала Юкава рассматривается поле ядерных сил по аналогии с электрическим взаимодействием. Взаимодействие между нуклонами включает в себя множество π– мезонов и должно включать в себя выводы, необходимые для решения задачи многих тел. Следовательно, ядерный потенциал не будет окончательно определен для области, где неупругие процессы играют существенную роль; кроме того, необходимо чтобы потенциал ядерного взаимодействия кроме обменного взаимодействия учитывал бы сильное отталкивание на малых расстояниях.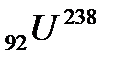 и кончается изотопом
и кончается изотопом  ;
; и кончается изотопом
и кончается изотопом  ;
; и кончается изотопом
и кончается изотопом 


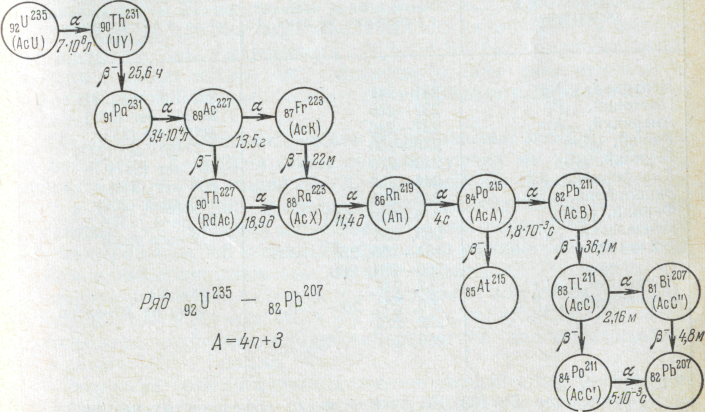

 -распадов, протон, входящий в состав ядра при этом превращается в нейтрон. Нейтроноизбыточные ядра также являются радиоактивными и превращаются в стабильные в результате
-распадов, протон, входящий в состав ядра при этом превращается в нейтрон. Нейтроноизбыточные ядра также являются радиоактивными и превращаются в стабильные в результате  -распадов, с превращением нейтрона ядра в протон.
-распадов, с превращением нейтрона ядра в протон.
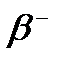 активные ядра; справа снизу α− активные ядра; у основания происходит деление ядер.
активные ядра; справа снизу α− активные ядра; у основания происходит деление ядер. , где
, где , где
, где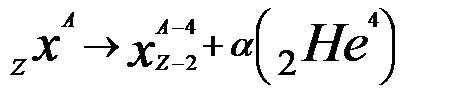

 .
. -4,48 МэВ (96%);
-4,48 МэВ (96%);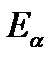 <9 МэВ, за среднее значение энергии принимается 6 МэВ.
<9 МэВ, за среднее значение энергии принимается 6 МэВ. , и пробегом
, и пробегом  , где А и В — постоянные величины. Если учесть, что пробег зависит от кинетической энергии, то закон Гейгера — Нэттола можно переписать и в таком виде
, где А и В — постоянные величины. Если учесть, что пробег зависит от кинетической энергии, то закон Гейгера — Нэттола можно переписать и в таком виде  .
. , то а α – частица с энергией порядка 6 МэВ не сможет пройти через потенциальный барьер. В рамках классической механики этот факт не может быть понят, однако квантовая механика показывает, что при любой конечной высоте
, то а α – частица с энергией порядка 6 МэВ не сможет пройти через потенциальный барьер. В рамках классической механики этот факт не может быть понят, однако квантовая механика показывает, что при любой конечной высоте раз, и вероятность прохождения частицы сквозь потенциальный барьер будет пропорциональна некоторому коэффициенту, называемого коэффициентом проницаемости барьера
раз, и вероятность прохождения частицы сквозь потенциальный барьер будет пропорциональна некоторому коэффициенту, называемого коэффициентом проницаемости барьера 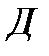 или просто прозрачностью, а вероятность пройти через барьер будет определяться
или просто прозрачностью, а вероятность пройти через барьер будет определяться 
 то согласно классическим законам частица должна отразиться, а согласно квантовым – частично отразиться и пройти.
то согласно классическим законам частица должна отразиться, а согласно квантовым – частично отразиться и пройти.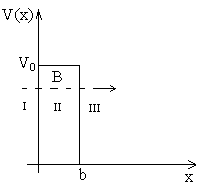
 ,
, ,
, .
. - сумме падающей и отраженной волн.
- сумме падающей и отраженной волн. .
.
 , и тогда решение этого уравнения имеет вид:
, и тогда решение этого уравнения имеет вид:  , где
, где 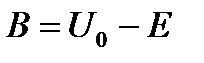 . Все постоянные
. Все постоянные 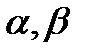
 определяются при выполнении условий непрерывности функции и ее производных на границе
определяются при выполнении условий непрерывности функции и ее производных на границе  : X=b эти условия приводят к:
: X=b эти условия приводят к: ,
, ,
,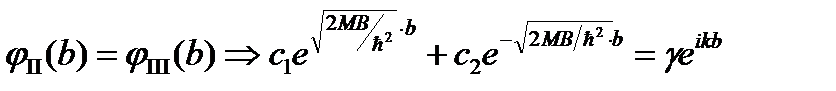 ,
,
 , то 4 уравнения нас устроят, хотя мы имеем 5 неизвестных. Решая первое и второе уравнение из четырех, мы получим
, то 4 уравнения нас устроят, хотя мы имеем 5 неизвестных. Решая первое и второе уравнение из четырех, мы получим  :
: 



 в 1-ое уравнение
в 1-ое уравнение























 ,
,
 и он оказался большим для частиц с меньшей массой и при
и он оказался большим для частиц с меньшей массой и при  получаем классический предел Д=0.
получаем классический предел Д=0. , таким образом мы приходим к зависимости, полученной Гейгером – Неттолом.
, таким образом мы приходим к зависимости, полученной Гейгером – Неттолом. , который по классическим оценка получается равной
, который по классическим оценка получается равной  . Ландау приравнял к частоте такого осциллятора расстояние между уровнями, которое равно среднему расстоянию
. Ландау приравнял к частоте такого осциллятора расстояние между уровнями, которое равно среднему расстоянию  рассматриваемыми между уровнями ядра и
рассматриваемыми между уровнями ядра и  ;
; (т.е. когда
(т.е. когда  , а
, а  ) и сопровождается испусканием электрона или позитрона или захватом ядром электрона. Период полураспада β− активных ядер меняется
) и сопровождается испусканием электрона или позитрона или захватом ядром электрона. Период полураспада β− активных ядер меняется  . β− распад наблюдается как у ядер с малым значением масс, так и с большим.
. β− распад наблюдается как у ядер с малым значением масс, так и с большим. распад. В этом случае ядро продукт испускает
распад. В этом случае ядро продукт испускает 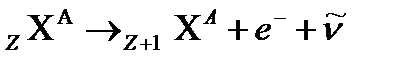


 распад. В этом случае ядро продукт испускает
распад. В этом случае ядро продукт испускает  или
или

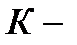 захват.
захват. 
 распадах освобождается энергия
распадах освобождается энергия 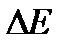 , равная
, равная .
.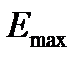 , которая и определяет верхнюю границу β − спектра. Теоретически, спектр должен быть дискретным, а экспериментально получили непрерывный. Встает вопрос, почему спектр непрерывный? Непрерывность β− спектра создает первую трудность на пути создания теории β− распада и приводит к нарушению закона сохранения энергии. Более того, при таком рассмотрении, оказалось, что нарушается закон сохранения количества движения (четности). Отметим, что свойства спина ядра быть целым или полуцелым определяется только четностью и нечетностью нуклонов, т.е. спин может изменяться только на целое число. В случае β− - распада
, которая и определяет верхнюю границу β − спектра. Теоретически, спектр должен быть дискретным, а экспериментально получили непрерывный. Встает вопрос, почему спектр непрерывный? Непрерывность β− спектра создает первую трудность на пути создания теории β− распада и приводит к нарушению закона сохранения энергии. Более того, при таком рассмотрении, оказалось, что нарушается закон сохранения количества движения (четности). Отметим, что свойства спина ядра быть целым или полуцелым определяется только четностью и нечетностью нуклонов, т.е. спин может изменяться только на целое число. В случае β− - распада  - изменение спина происходит не на целое число. Выход из этих трудностей был предложен В. Паули в 1931 г. Паули высказал гипотезу о существовании частицы с нулевой массой покоя и спином равным 1/2, которую он назвал нейтрино. Эта частица создается и испускается вместе с β− частицей и решает обе трудности. Во-первых, в каждом акте распада ядро отдает одну и ту же энергию
- изменение спина происходит не на целое число. Выход из этих трудностей был предложен В. Паули в 1931 г. Паули высказал гипотезу о существовании частицы с нулевой массой покоя и спином равным 1/2, которую он назвал нейтрино. Эта частица создается и испускается вместе с β− частицей и решает обе трудности. Во-первых, в каждом акте распада ядро отдает одну и ту же энергию  выполняется закон сохранения спина. В соответствии с законом сохранения заряда электрический заряд должен быть равен нулю, а масса значительно меньше массы электрона, т.к. нейтрино уносит большую часть энергии и спин нейтрино должен быть полуцелым. Благодаря слабому взаимодействию с веществом (одна ионизация при прохождении через весь земной шар) нейтрино и антинейтрино долгое время были неуловимы и только через 25 лет частицы были обнаружены. Главной особенностью β− распада является то, что он обусловлен не ядерными, не электромагнитными, а слабыми взаимодействиями, интенсивность которых на 24 порядка меньше ядерного взаимодействия.
выполняется закон сохранения спина. В соответствии с законом сохранения заряда электрический заряд должен быть равен нулю, а масса значительно меньше массы электрона, т.к. нейтрино уносит большую часть энергии и спин нейтрино должен быть полуцелым. Благодаря слабому взаимодействию с веществом (одна ионизация при прохождении через весь земной шар) нейтрино и антинейтрино долгое время были неуловимы и только через 25 лет частицы были обнаружены. Главной особенностью β− распада является то, что он обусловлен не ядерными, не электромагнитными, а слабыми взаимодействиями, интенсивность которых на 24 порядка меньше ядерного взаимодействия.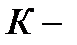 захвата подтверждает тот факт, что захватываются электроны ядрами;
захвата подтверждает тот факт, что захватываются электроны ядрами; - для нейтрино и
- для нейтрино и  - для протона, то волновые функции, описывающие состояние частиц
- для протона, то волновые функции, описывающие состояние частиц  ,
,  . Ввиду, слабого взаимодействия нейтрино с веществом его волновую функцию можно считать плоской волной. Предположим, что вероятность излучения зависит от вероятности того, что электрон и нейтрино находятся в ядре
. Ввиду, слабого взаимодействия нейтрино с веществом его волновую функцию можно считать плоской волной. Предположим, что вероятность излучения зависит от вероятности того, что электрон и нейтрино находятся в ядре  , вероятность излучения зависит и от других множителей, природа которых не ясна. Одним из них является матричный элемент
, вероятность излучения зависит и от других множителей, природа которых не ясна. Одним из них является матричный элемент  , который связан с переходами из начального в конечное состояние.
, который связан с переходами из начального в конечное состояние. , где
, где  - начальное и конечное состояния нуклонов. Когда они идентичны
- начальное и конечное состояния нуклонов. Когда они идентичны  , а чем больше они отличаются, тем меньше
, а чем больше они отличаются, тем меньше  . Матричный элемент может быть представлен в векторном виде, выбор матричного элемента определяется правилами отбора. согласно квантовой механике, вероятность излучения электрона в единицу времени можно определить следующим образом:
. Матричный элемент может быть представлен в векторном виде, выбор матричного элемента определяется правилами отбора. согласно квантовой механике, вероятность излучения электрона в единицу времени можно определить следующим образом:  , где
, где - величина, характеризующая силу взаимодействия или интенсивность β−распада;
- величина, характеризующая силу взаимодействия или интенсивность β−распада; - плотность конечных состояний;
- плотность конечных состояний; , где
, где интегральная функция по энергии;
интегральная функция по энергии; , где
, где 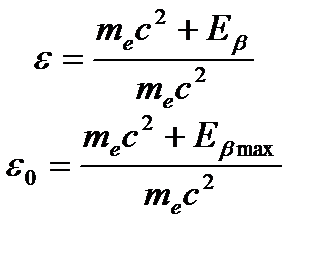
 кривая резко поднимается вверх в силу корня, а в конце квадратично примыкает к оси абсцисс при ε=ε0. Такая же картина справедлива и для β±−частиц, т.к. нигде не оговаривается заряд вылетевших частиц; ясно, что влияние кулоновского потенциала на β − распад будет заметен для малых энергий, когда кулоновское взаимодействие и кинетическая энергия вылетевшего электрона одного порядка. Следовательно, учет этого приводит к увеличению β − электронов в области малых энергий, хотя, при
кривая резко поднимается вверх в силу корня, а в конце квадратично примыкает к оси абсцисс при ε=ε0. Такая же картина справедлива и для β±−частиц, т.к. нигде не оговаривается заряд вылетевших частиц; ясно, что влияние кулоновского потенциала на β − распад будет заметен для малых энергий, когда кулоновское взаимодействие и кинетическая энергия вылетевшего электрона одного порядка. Следовательно, учет этого приводит к увеличению β − электронов в области малых энергий, хотя, при  с экспериментальным β-спектром.
с экспериментальным β-спектром. и максимальной энергии
и максимальной энергии  и
и  .
. - для всех β-превращений при одинаковых матричных элементах.
- для всех β-превращений при одинаковых матричных элементах.
 .
. , характеризующая К - мезона близка к
, характеризующая К - мезона близка к  , где
, где - частица, падающая на ядро;
- частица, падающая на ядро; - исходное ядро;
- исходное ядро; - частица, полученная в результате взаимодействия;
- частица, полученная в результате взаимодействия; - ядро – продукт.
- ядро – продукт.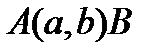 .
. и
и  . Частицы, возникшие при радиоактивном распаде, могут вызвать реакции только на легких ядрах, для которых высота кулоновского потенциального барьера имеет порядок 10 МэВ. В этом случае вероятность реакций
. Частицы, возникшие при радиоактивном распаде, могут вызвать реакции только на легких ядрах, для которых высота кулоновского потенциального барьера имеет порядок 10 МэВ. В этом случае вероятность реакций  . Примером такой реакции может быть реакция, осуществленная Резерфордом в 1919 г.
. Примером такой реакции может быть реакция, осуществленная Резерфордом в 1919 г.  или
или  При этих реакциях, как правило, образуются стабильные ядра.
При этих реакциях, как правило, образуются стабильные ядра. или
или 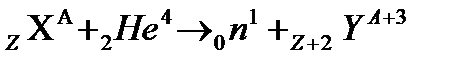
 или
или  .
. или
или  .
. - квантов.
- квантов. ,
,  ,
,  ,
, 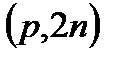 ,
, 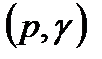 .
. . Примером такой реакции может быть реакция, осуществляемая с помощью частиц, ускоренных на ускорителях в 1932 г.
. Примером такой реакции может быть реакция, осуществляемая с помощью частиц, ускоренных на ускорителях в 1932 г. 

 . Исследование этих реакций помогло выяснить механизм протекания ядерных реакций
. Исследование этих реакций помогло выяснить механизм протекания ядерных реакций  .
. . Реакции этого типа всегда эндоэнергетические с порогом порядка (1 - З) МэВ. Как правило, ядро - продукт, приобретая добавочный положительный заряд, проявляет β+ - или К - активность. Примером такой реакции может быть реакция
. Реакции этого типа всегда эндоэнергетические с порогом порядка (1 - З) МэВ. Как правило, ядро - продукт, приобретая добавочный положительный заряд, проявляет β+ - или К - активность. Примером такой реакции может быть реакция 
 . Примером такой реакции может быть реакция
. Примером такой реакции может быть реакция 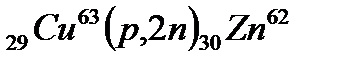

 . Примером такой реакции может быть реакция
. Примером такой реакции может быть реакция  . Данная реакция служит источником γ-лучей до 17 МэВ, в результате чего получаются жесткие лучи.
. Данная реакция служит источником γ-лучей до 17 МэВ, в результате чего получаются жесткие лучи.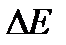 = 2,23 МэВ). Нуклоны в ядре дейтрона находятся на довольно большом расстоянии друг от друга (~4-10~13 см), и распределение заряда в нем чрезвычайно «асимметрично».
= 2,23 МэВ). Нуклоны в ядре дейтрона находятся на довольно большом расстоянии друг от друга (~4-10~13 см), и распределение заряда в нем чрезвычайно «асимметрично». и
и  .
. . Примером служит реакция срыва, теоретически рассмотренная Оппенгеймером
. Примером служит реакция срыва, теоретически рассмотренная Оппенгеймером  .
.  .
. . Примером служит реакция
. Примером служит реакция 

 по следующей схеме
по следующей схеме  . Примером служит реакция
. Примером служит реакция 


