
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитный момент P (Метод Рабби)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Экспериментальное определение магнитного момента ядра различны и используются в основном методика помещения атома во внешнее магнитное поле. В этом случае магнитный момент ядра будет взаимодействовать как с магнитным полем электронной оболочки
Часто используются «сильные» магнитные поля. Сильным полем
Сильное поле как бы разрывает связь между магнитным моментом ядра и магнитным полем электронной оболочки, в результате чего ядерный момент Рассмотрим один из наиболее распространенных и наиболее точных методов определения магнитных моментов ядер метод Рабби, или метод магнитного резонанса. Идея метода заключается в переориентации магнитных моментов атомов, молекул и ядер в постоянном магнитном поле при наличии осциллирующего или вращающегося магнитного поля. Установка состоит из трех полей: первое и третье поле неоднородн Рассмотрим схему эксперимента Рабби: имеются 3 поля, первое и третье резко неоднородны, одинаковы по своей величине, но направления градиентов полей противоположны
В третьем поле действует сила, направленная вниз,
Как узнать о том, что произошла переориентация? На экране детектора будет провал интенсивности при
Домашнее задание: 1. Рассмотреть и изучить магнитный момент нейтрона - Метод Блоха. Энергия связи ядер Энергия связи равна работе, которую нужно затратить, чтобы разделить ядро на составные части: Вспомним, что
Где Z - число протонов; (A-Z)- число нейтронов M(A,Z)- масса собранного ядра, она выражается в МэВ: для
Во многих случаях, например, для сравнения устойчивости ядер, пользуются понятием удельной энергии связи — ε, характеризующей среднюю энергию связи одного нуклона в ядре. Величина ε равна отношению полной энергии к полному числу нуклонов в ядре А: Анализ экспериментальных данных позволяет построить кривую зависимости
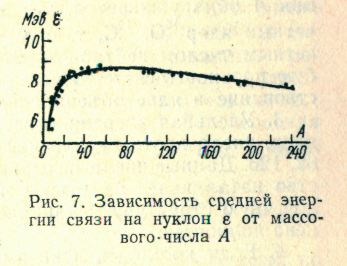
Рис. 1.
Из приведенной на рис.1 экспериментальной зависимости ε(А)можно видеть, что при малых А величина ε меняется неравномерно и имеет аномально малую величину по сравнению со средним ее значением. Удельная энергия связи слабо зависит от А,меняется от 7.4 до 8.8 МэВ. Приблизительное постоянство удельной энергии связи обусловлено короткодействующим характером ядерных сил; так, для дейтрона ε =1,1 МэВ. Далее, величина ε медленно возрастает до значения 8,8 МэВ. Из хода зависимости ε от А следует несколько очень важных выводов, на которых должна основываться теория ядерных сил. 1. Самые легкие ядра отличаются аномально малыми значениями энергии. Для примера достаточно сказать, что обусловленная ядерными силами удельная энергия связи простейшего ядра — дейтрона — равна 1,1 МэВ, 2. За среднюю удельную энергию связи выбирают величину, равную 8 МэВ. Тогда получается, что ∆W~8А МэВ., т.к. Перечислим свойства ядерных сил и укажем, какие экспериментальные факты свидетельствуют о существовании каждого из этих свойств. 1. Ядерные силы обладают свойством насыщения, т.е. каждый нуклон взаимодействует не со всеми окружающими нуклонами, а только с ограниченным их числом, ∆W~А. Если бы каждый нуклон взаимодействовал со всеми окружающими, то это выражение имело бы вид ∆W~А2. 2. Максимальная удельная энергия связи наступает в области железа А >50, что соответствует области стабильных ядер. Следовательно, легким ядрам выгодно сливаться в тяжелые и стабильные с выделением термоядерной энергии, а тяжелым выгодно делиться, с выделением атомной энергии. 3. Интенсивность ядерных сил по сравнению с кулоновскими силами – большая (8 МэВ - 1 МэВ) 4. Удельная энергия связи имеет небольшие максимумы для ядер, число протонов и нейтронов у которых равно 2, 8, 20, 50, 82, 126. – эти числа назвали, «магическими» т.к. при этих значениях ядра обладают особой устойчивостью. Этот факт приписывается проявлению оболочечной структуры ядра. Итак, атомные ядра могут быть стабильными и нестабильными. Рассмотрим вопрос об устойчивости ядер по отношению к распаду. Проанализируем процесс распада ядра А на 2 составляющих: В и С - продукты распада. В случае, когда М(А)<М(В)+М(С), распад Например, для тяжелых ядер (у которых Z>82), происходит α– распад; М(А, Z)> M(A-4, Z-2) +M(2He4) – т.е. тяжелое ядро не устойчиво к испусканию α– частиц. Таким образом, нуклоны находятся внутри ядра в состоянии, отличающемся от их свободного состояния и это связано с влиянием соседних нуклонов. Энергия связи - это разность энергии сложного ядра и совокупности, достаточно удаленных друг от друга покоящихся нуклонов.
Размеры атомных ядер Существует множество способов, позволяющих произвести оценку размеров ядра. Разные методы приводят к различающимся экспериментальным результатам, однако, порядок величины во всех случаях остается одинаковым. Первые оценки были сделаны из опыта по рассеянию Столкновение Потенциальная энергия на расстоянии rмежду частицами или работа отталкивания будет выражаться как: Кинетическая энергия Все существующие методы определения радиуса ядра делятся на 2 типа: 1. Методы, регистрирующие наличие ядерного вещества; 2. Методы чисто электромагнитные, т.е. связанные с наличием определенного заряда внутри ядра.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 , так и с внешним магнитным полем
, так и с внешним магнитным полем  , и энергия взаимодействия будет равна:
, и энергия взаимодействия будет равна:
 ,будем называть поле, энергия взаимодействия которого с магнитным моментом электронной оболочки
,будем называть поле, энергия взаимодействия которого с магнитным моментом электронной оболочки  атома значительно больше энергии взаимодействия магнитного момента ядра
атома значительно больше энергии взаимодействия магнитного момента ядра 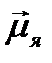 с полем электронной оболочки.
с полем электронной оболочки.

 и момент электронной оболочки
и момент электронной оболочки  прецессируют вокруг вектора внешнего поля
прецессируют вокруг вектора внешнего поля 

 - поле однородное и к нему приложено перпендикулярно переменное осциллирующее поле. Суть метода заключается в принудительной переориентации магнитного момента ядра резонансным высокочастотным полем. В первом поле действует сила, направленная вверх
- поле однородное и к нему приложено перпендикулярно переменное осциллирующее поле. Суть метода заключается в принудительной переориентации магнитного момента ядра резонансным высокочастотным полем. В первом поле действует сила, направленная вверх
 , при этом
, при этом 
 Следовательно, пучок в поле
Следовательно, пучок в поле  повторяет траекторию пучка в поле
повторяет траекторию пучка в поле  , только в противоположном направлении и потому попадает в детектор. Что же происходит в поле
, только в противоположном направлении и потому попадает в детектор. Что же происходит в поле  ? В методе Рабби перпендикулярно полю
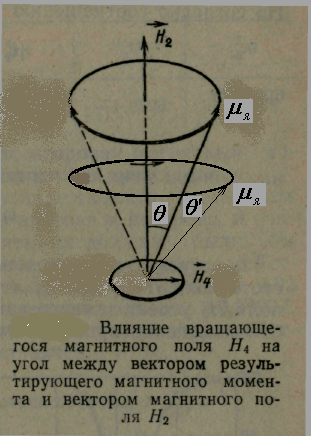
? В методе Рабби перпендикулярно полю  . В чем же смысл резонансного опрокидывания? Если протон имеет магнитный момент, то его магнитный момент осциллирует относительно поля
. В чем же смысл резонансного опрокидывания? Если протон имеет магнитный момент, то его магнитный момент осциллирует относительно поля  вокруг направления магнитного поля с постоянным углом наклона, подобно волчку в поле силы тяжести. Угол между
вокруг направления магнитного поля с постоянным углом наклона, подобно волчку в поле силы тяжести. Угол между 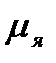 и
и  . Следовательно:
. Следовательно:  и в первом и в третьем поле. Потому
и в первом и в третьем поле. Потому  . Взаимодействие между
. Взаимодействие между  и
и 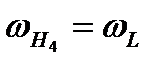 , произойдет переориентация магнитного момента протона относительно направления постоянного магнитного поля
, произойдет переориентация магнитного момента протона относительно направления постоянного магнитного поля  . Взаимодействие между магнитным моментом
. Взаимодействие между магнитным моментом  на
на  . Мы будем иметь
. Мы будем иметь  , т.е.
, т.е.  , следовательно сила действующая в третьем поле изменится на
, следовательно сила действующая в третьем поле изменится на 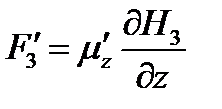 , т.е.
, т.е.  . Подставив значения Ларморовской прецессии, можно определить гиромагнитный множитель, а следовательно и магнитный момент
. Подставив значения Ларморовской прецессии, можно определить гиромагнитный множитель, а следовательно и магнитный момент  .
. Эксперимент дал величину магнитного момента протона, он оказался равным:
Эксперимент дал величину магнитного момента протона, он оказался равным:  .
. , т.к. частицы изменят траекторию в связи с изменением силы F3. Сила
, т.к. частицы изменят траекторию в связи с изменением силы F3. Сила 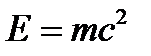 , а
, а 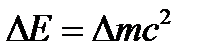 и поэтому
и поэтому ,
,
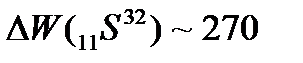 МэВ
МэВ МэВ
МэВ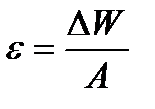 . Чем больше значение ε, тем устойчивее ядро. Чтобы ядро было устойчивым, его масса должна быть меньше суммы масс любой пары ядер, на которые можно разделить это ядро. В настоящее время известно, что нуклоны внутри ядра находятся в состояниях, отличающихся от их свободного состояния, что связано с влиянием других нуклонов. Типичная картина – это обмен виртуальными мезонами. Энергия связи – это есть разность энергии сложного ядра и совокупности достаточно удаленных друг от друга покоящихся нуклонов.
. Чем больше значение ε, тем устойчивее ядро. Чтобы ядро было устойчивым, его масса должна быть меньше суммы масс любой пары ядер, на которые можно разделить это ядро. В настоящее время известно, что нуклоны внутри ядра находятся в состояниях, отличающихся от их свободного состояния, что связано с влиянием других нуклонов. Типичная картина – это обмен виртуальными мезонами. Энергия связи – это есть разность энергии сложного ядра и совокупности достаточно удаленных друг от друга покоящихся нуклонов.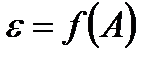

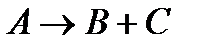 запрещен законом сохранения энергии, т.к любая система стремится в состояние с минимальной энергией. В случае когда М(А)>М(В)+М(С), распад разрешен законом сохранения энергии. Итак, энергетическое условие распада ядра
запрещен законом сохранения энергии, т.к любая система стремится в состояние с минимальной энергией. В случае когда М(А)>М(В)+М(С), распад разрешен законом сохранения энергии. Итак, энергетическое условие распада ядра  можно записать таким образом М(А)>М(В)+М(С).
можно записать таким образом М(А)>М(В)+М(С). 2. Стабильно ли ядро лития к следующему распаду:
2. Стабильно ли ядро лития к следующему распаду: 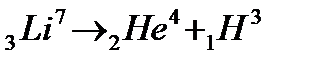
 – частиц на ядрах (опыты Резерфорда). Отметим, что аномально большие углы рассеяния
– частиц на ядрах (опыты Резерфорда). Отметим, что аномально большие углы рассеяния  или, в нашем случае
или, в нашем случае  .
.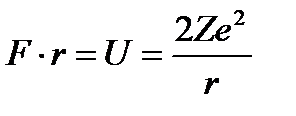
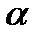 - частицы на большом расстоянии от ядра равна
- частицы на большом расстоянии от ядра равна 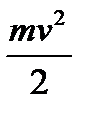 . При прямом попадании на рассеивающий центр,
. При прямом попадании на рассеивающий центр, 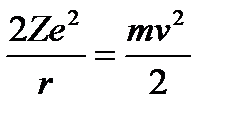 . Это и есть оценка размера ядра, которая использовалась Резерфордом; опыт показал, что величина r0 для ядер тяжелых элементов имеет порядок 10-12см.
. Это и есть оценка размера ядра, которая использовалась Резерфордом; опыт показал, что величина r0 для ядер тяжелых элементов имеет порядок 10-12см.


