Методы поиска решений в пространстве состояний

 

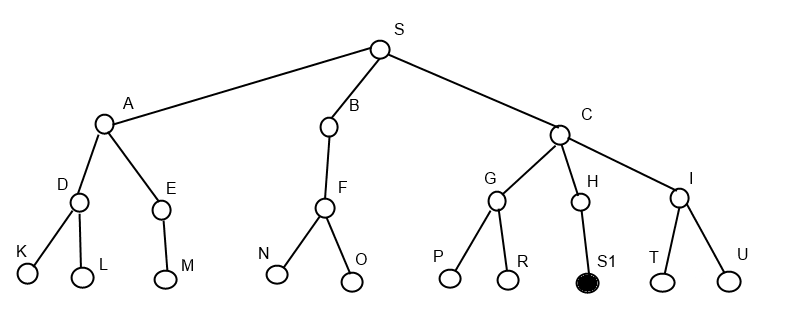
Методы поиска решений в пространстве состояний:

1) Методы слепого перебора (не информированные):

*метод поиска в ширину

*метод поиска в глубину

*метод равных цен.

2) Методы направленного перебора (эвристические).

Поиск решений в пространстве состояний сводится к нахождению пути на графе представляющем начальное состояние вершины к вершине представляющей целевое состояние.

Списки вершин графа:

1.Список закрыт (содержит вершины уже исследованные и не представляющие интереса в данный момент).

2.Список открыт (содержит вершины, которые нужно исследовать на следующих шагах).

 

 

Метод поиска в ширину

 

Алгоритм методов поиска в ширину:

 

Открыт	Закрыт
S
A,B,C	S
B,C,D,E	S,A
C,D,E,F	S,A,B
D,E,F,G,H,I	S,A,B,C
E,F,G,H,I,K,L	S,A,B,C,D
F,G,H,I,K,L,M	S,A,B,C,D,E
G,H,I,K,L,M,N,O	S,A,B,C,D,E,F
H,I,K,L,M,N,O,P,R	S,A,B,C,D,E,F,G
I,K,L,M,N,O,P,R,S1	S,A,B,C,D,E,F,G,H

S1 H C S

Метод поиска в глубину

 

Алгоритм метода поиска в глубину:

Граничная глубина- т.е. нет больше приемников у вершины.

Открыт	Закрыт
S
A,B,C	S
D,E,B,C	S,A
K,L,E,B,C	S,A,D
L,E,B,C	S,A,D,K
E,B,C	S,A,D,K,L
M,B,C	S,A,D,K,L,E
B,C	S,A,D,K,L,E,M
F,C	S,A,D,K,L,E,M,B
N,O,C	S,A,D,K,L,E,M,B,F
O,C	S,A,D,K,L,E,M,B,F,N
C	S,A,D,K,L,E,M,B,F,N,O
G,H,I	S,A,D,K,L,E,M,B,F,N,O,C
P,R,H,I	S,A,D,K,L,E,M,B,F,N,O,C,G
R,H,I	S,A,D,K,L,E,M,B,F,N,O,C,G,P
H,I	S,A,D,K,L,E,M,B,F,N,O,C,G,P,R
S1,I	S,A,D,K,L,E,M,B,F,N,O,C,G,P,R,H

S1 H C S

 

Метод равных цен

Метод равных цен является более общим вариантом метода поиска в ширину. Он позволяет найти путь от начальной вершины к целевой, стоимость которого минимальна, при этом задаются стоимости с(n_i,n_j).

Алгоритм поиска решений методом равных цен отличается от алгоритма поиска в ширину тем, что из списка ОТКРЫТ выбирается та вершина для очередного раскрытия, которая имеет минимальную стоимость пути до неё.

 

ОТКРЫТ	ЗАКРЫТ
S(0)
A(2),B(1),C(5)	S(0)
A(2),C(5),D(3),E(5),F(3)	S(0), B(1)
C(5),D(3),E(5),F(3),G(4),H(6)	S(0), B(1),A(2)
C(5),E(5),F(3),G(4),H(6),L(7),N1(3)	S(0), B(1),A(2), D(3),
Путь: N1(3) D(3) A(2) B(1) S(0)

 

Общая процедура поиска на графе

Если перебор осуществляется не на деревьях, а на произвольных графах алгоритмы поиска усложняются.

Процедура коррекции указателя

- это вершины находятся в списке ЗАКРЫТ. Рассматриваем вершину 1. При ее раскрытии приемника является вершина 2, которая уже находится в списке ЗАКРЫТ. В этом случае необходимо провести процедуру корреляции указателей, так как минимальный путь к вершине проходит через вершину 1. А затем провести процедуру корреляции указателей для потомков вершины 2 из списка ЗАКРЫТ(в примере вершина 5).

 

 

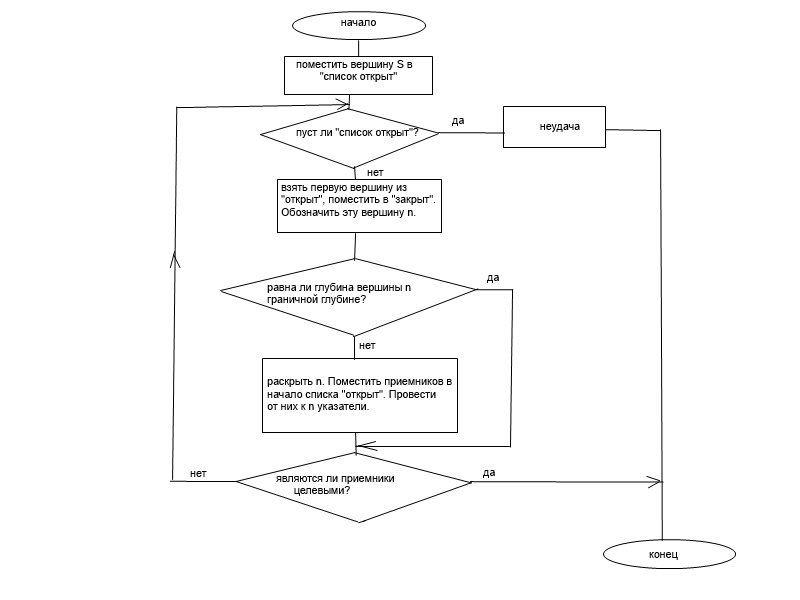
Алгоритм общего поиска на графах

 

1 – Создать граф поиска, состоящий лишь из начальных вершин s, занести s в список ОТКРЫТ.

2-Создать список ЗАКРЫТ, который в начале ПУСТ.

3- Пуст ли список ОТКРЫТ?

4-Выбрать 1-ую вершину из списка ОТКРЫТ, обозначить через n и перенести ее в список ЗАКРЫТ.

5- N является целевой вершиной?

6-Раскрыть вершину n множество ее приемников ранее не входящих в данный граф поиска в список ОТКРЫТ.

7-Для тех приемников, которые не входили в граф поиска провести к n указатели. Для тех приемников, которые уже были в списке ОТКРЫТ/ЗАКРЫТ провести корреляцию процедуры указателей. Если рассчитанная стоимость к этим приемникам через вершину n будет меньше стоимости ранее определенного пути.

8 – упорядочить список ОТКРЫТ в соответствии с выбранной стратегией управления(т.е.будет определяться).

 

 

Эвристические методы поиска решений на графе

Недостатками метода слепого перебора является низкое быстродействие, так как выполняется перебор большого количества вариантов.

Чтобы содействовать сокращению поиска используется информация о решаемой задаче. Такая информация называется эвристической. Эвристические методы основаны на понятии оценочной функции. Эта функция используется для упорядочения вершин в списке открыт в процедуре общего поиска на графе. При этом раскрытию выбирается та вершина для которой оценочная функция меньше, а все вершины в списке открыт располагаются в порядке возрастания оценочной функции.

F(n)=d(n)+w(n), где F – оценочная функция, n – конкретная вершина, d – глубина, w – число находящихся не на своём месте для данного состояния системы.

 

В результате решение задачи эвристического метода на графе находится оптимальный путь.

Логические модели представления знаний