
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Извлечение ответа методом резолюцииСодержание книги
Поиск на нашем сайте
Метод резолюции реализует два этапа решения задач. Первый этап: доказывается теорема следует ли целевая функция G из множества ПФ Е, то есть существует ли такой х для которого G(x). Второй этап: найти значение этого существующего х. 1 этап: доказывается теорема, следует ли целевая функция G из множества ПФ Е, т.е. существует ли такой Х для которого G(x) (ƎxG(x)) 2 этап: найти значение этого существующего x. Пример: Если Саша всегда ходит за Машей, а Маша находится в кино, то где Саша?. Находится (Маша, Кино) – факт. На языке предикатов факт: находится (маша, кино) Правило: ∀x(находится(маша,Х))→находится(саша,Х) Аксиомы: nahod(masha,kino) ∀X(nahod(masha,X))→nahod(sasha,X) Целевая функция: ƎX(nahod(sasha,X)) Теорема: ƎX(nahod(sasha,X)) Проведем доказательство теоремы методом резолюции. Доказательство: Согласно следствию из основной теоремы логического вывода ПФ F1&F2&…Fn&G –противоречие G=ƎX(nahod(sasha,X)) G=(ƎX(nahod(sasha,X))) не существует ни одного Х, где находится Саша. Согласно формуле ƎXP(X)=(∀XP(X)) ∀X(nahod(sasha,X)) (ƎX(nahod(sasha,X)))= ∀X(nahod(sasha,X)) Образуем множество Е ПФ состоящих из множества исходных предложений баз знаний объединенного с множеством предложений отрицания целевой функции. Е=F∪G F={F1,F2}, где В результате множество Е имеет вид: Е={nahod(masha,kino), ∀X(nahod(masha,X))→nahod(sasha,X), ∀X(nahod(sasha,X)))} Согласно закону логики A→B=A∨B, преобразуем ПФ в соответсвии с правилами баз знаний. ∀X(nahod(masha,X))→nahod(sasha,X) = ∀X(nahod(masha,X)) ∨ nahod(sasha,X)) Опускаем знаки кванторов во всех ПФ входящих в множество {Е}. В результате множество Е примет вид: E={nahod(masha,kino),(nahod(masha,X)∨nahod(sasha,X)),(nahod(sasha,X))} Далее осуществляется вычисление резольвенты по формуле: rij {{Li } – { li }}N’ ∪ {{Mi}-{mi}}N’ Шаг 1: 1) Принимаем за множество Li отрицание цели {Li}={nahod(sasha,X)} 2) Выбираем за {li}⊂{Li} ={nahod(sasha,X)} 3) Принимаем за множество {Mi} преобразованную аксиому F2 {Mi}={nahod(masha,X) ∨ nahod(sasha,X)} 4) Принимаем за {mi}⊂{Mi}, где {li}N’={mi}N’ {mi}={nahod(sasha,X)} 5) Определим ci ={Li}-{li} ci={ nahod(sasha,X)N’-{ nahod(sasha,X)}N’={} cj = {Mi}-{mi} cj={ nahod(masha,X)∨ nahod(sasha,X)}N’-{nahod(sasha,X)}={ nahod(masha,X)} Вычислим rij = {ci}∪{cj}={}∪{ nahod(masha,X)}
Рисунок -дерево опровержения
Шаг 2: Принимаем за множество Li-отрицание. 1) Li={nahod(masha,X)} 2) Выбираем за {li}⊂{Li} {li}={ nahod(masha,X)} 3) Выбираем за множество Mi – аксиому F1={ nahod(masha,X)} {Mi}={ nahod(masha,kino)} 4) Выбираем за {mi} ⊂ {Mi}, где {li}N’={mi}N’ НОУ N’ = {kino/x} {mi}N’={ nahod(masha,kino)} {li}N’={ nahod(masha,X)} 5) Определим ci и cj ci={Li}N’- {li}N’ ={ nahod(masha,kino)}N’ -{ nahod(masha,kino)}N’={ } cj={Mi}N’-{mi}N’ cj={ nahod(masha,kino)}N’-{ nahod(masha,kino)}N’={ } Тогда rij=ci ∨ cj={ } { }
Результат: резольвента rij является пустым множеством { }, следовательно множество Е является противоречивым ⇒ существует такой Х, что ∃Xnahod(sasha,X) Для извлечения ответа из дерева опровержения методом резолюции строится дерева доказательства. Алгоритм построения дерева доказательства 1) Добавить каждой ПФ(предложению), возникающий из отрицания целевой функции её собственное отрицание. 2) Следуя структуре дерева опровержения выполнить те же самые резолюции, что и раньше до тех пор пока в корневой вершине не будут построены некоторые предложения 3) Использовать предложения в корневой вершине в качестве ответного утверждения. Таким образом, извлечение ответа состоит в преобразовании дерева опровержений с пустым множеством в корневой вершине в дерево доказательства с утверждением в вершине. При таком преобразовании каждое предложение возникающее в результате целевой функции преобразовывается в тавтологию согласно закону двойного отрицания, то утверждение, стоящее в корневой вершине дерева доказательства следует из тавтологии и аксиом, а следовательно оно следует из самих аксиом и является истинным утверждением Шаг 1. 1) Добавляем к каждому предложению, возникающей из отрицания целевой функции его собственное отрицание и строим множество {Li} {Li}={nahod(sasha,X)∨(nahod(sasha,X))} Преобразуем {Li} по закону логики А=A, а так же учитываем что A∨A = Истина, Где А=nahod(sasha,X) {Li}={nahod(sasha,X)∨(nahod(sasha,X))} 2) {li}⊂{Li}, {Li}={ nahod(sasha,X)} 3) Принимаем {Mi} аксиому F2, {Mi} = { nahod(masha,X)∨(nahod(sasha,X)} 4) {mi}⊂{Mi}, где {li}N’={mi}N’={ nahod(sasha,X)} 5) ci={{Li}-{li}}N’={ nahod(sasha,X)∨ nahod(sasha,X)}-{ nahod(sasha,X)}={ nahod(sasha,X)} cj={{Mi}-{mi}}={ nahod(masha,X)∨ nahod(sasha,X)} - { nahod(sasha,X)}={ nahod(masha,X)} rij=ci ∪ cj = { nahod(sasha,X)} ∪ { nahod(masha,X)} = { nahod(sasha,X)∨ nahod(masha,X)}
Шаг 2. 1.Принимаем за множество 2.Выбираем за 3.Принимаем за 4
N= mi = li= 5.Ci= - Cj = rij = rij =Ci rij =
Рисунок – Дерево отвержения НОУ = Представление процесса логического вывода с помощью И/ИЛИ дерева И/ИЛИ дерево представляет собой рисунок:
Нейронные сети
Одним из наиболее перспективной ИИ системы. Это многопроцессорная система. 1.Недостатки и преимущества использования нейронных сетей Преимущества: 1. 1.Параллельная обработка информации. Резко сокращается время на задачу 2. 2.Надежность функционирования 3. 3.Возможность обучения 4. 4.Способность решать неформализованные задачи. Не численные задачи, условие которых заданы не логически Нейронные сети реализуются на нейрокомпьютерах. Они могут менять свое поведение в зависимости от составления окружающей среды. После анализа входных сигналов они самонастраиваются и обучаются. Первые нейронный сети создали в 50ые годы XX века. Первые искусственные нейронные сети в 70ые годы XX века. А в 90ые годы появился нейрокомпьютер на одном кристалле. Пример: Многослойная, полносвязная нейронная сеть прямого распространения сигнала. Полносвязная сетью называется – многослойная структура для которой каждый нейрон производит слоя связанные со всеми нейронами предыдущего слоя. А в случае первого слоя со всеми ходами нейронной сети. Прямое распределение сигнала обозначает, что данная нейронная сеть не содержит петель.
Выход нейрона слоя i+1 рассчитывается как функция от суммы произведения веса на dход со слоя i это x. N –число весов. Обучение нейронных сетей: под обучением нейронных сетей понимается: 1) Процесс настройки архитектуры сетей (структуры связей между нейронами) 2) Настройка весов в ходах каждого нейрона. Обучение нейронной сети осуществляется на известной выборке. Процесс обучения проходит по определенному алгоритму. Существует 3 вида обучения: 1) с учителем – известны правильные ответы к каждому входному примеру. Веса подстраиваются так, чтобы минимизировать ошибку; 2) обучение без учителя – распределение образцов по категориям за счет раскрытия внутренней структуры данных; 3) смешанное обучение – комбинация первого и второго. Недостатки использования нейронных сетей: 1) Надежность работы. Искусственные нейронные сети дают высокий процент ошибок и не используются в ситуациях касающихся жизни людей, а выступают в качестве дополнительного средства. 2) Традиционные нейронные сети не способны объяснить как они решают задачу, что затрудняет проверку достоверности результата. 3) Высокая стоимость. Преодоление этих недостатков - это комбинация нейронных сетей и экспертных систем. Простые вопросы решает нейронная сеть, а более сложные передаются в экспертную систему. Преимущества нейронных сетей: 1) Возможность работы в условиях непригодных для человека. 2) Решение задач в реальном времени. 3) Возможность решать интеллектуальные задачи без участия человека. Области применения нейронных сетей: 1) Оборонная промышленность. Решение зада, распознавание образов. 2) Сети и телекоммуникации – расчет трафика между узлами сети. 3) Информационные технологии. Определение тематики текстовых сообщений. 4) Реклама и маркетинг. 5) Экономика и финансы. Используется в банках для отслеживания клиентов при использовании кредитных и банковских карт. 6) Здравоохранение. Проверка и анализ слуха у грудных детей Перспективы развития нейронных сетей: 1) «Умные дома». 2) Разработка нейрокомпьютеров, способных общаться на естественном для человека языке. 3) Использование нейронных сетей в роботах.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.65 (0.009 с.) |


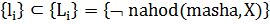
 аксиому F1 = =
аксиому F1 = = 






 Ni
Ni
 Cj
Cj


 V
V
 V
V



 =f
=f  - Формула одного нейрона
- Формула одного нейрона


