
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм поиска компонент связности в графеСодержание книги Поиск на нашем сайте
Форд-Беллман struct edge { int a, b, cost; };
int n, m, v; vector<edge> e; const int INF = 1000000000;
void solve() { vector<int> d (n, INF); d[v] = 0; for (;;) { bool any = false; for (int j=0; j<m; ++j) if (d[e[j].a] < INF) if (d[e[j].b] > d[e[j].a] + e[j].cost) { d[e[j].b] = d[e[j].a] + e[j].cost; any = true; } if (!any) break; } // вывод d, например, на экран }
Флойд-Уоршелл Дан ориентированный или неориентированный взвешенный граф Предполагается, что граф не содержит циклов отрицательного веса (тогда ответа между некоторыми парами вершин может просто не существовать — он будет бесконечно маленьким). for (int k=0; k<n; ++k) for (int i=0; i<n; ++i) for (int j=0; j<n; ++j) if (d[i][k] < INF && d[k][j] < INF) d[i][j] = min (d[i][j], d[i][k] + d[k][j]);
BFS В результате поиска в ширину находится путь кратчайшей длины в невзвешенном графе, т.е. путь, содержащий наименьшее число рёбер. Алгоритм работает за vector < vector<int> > g; // граф int n; // число вершин int s; // стартовая вершина (вершины везде нумеруются с нуля) queue<int> q; q.push (s); vector<bool> used (n); vector<int> d (n), p (n); used[s] = true; p[s] = -1; while (!q.empty()) { int v = q.front(); q.pop(); for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i]; if (!used[to]) { used[to] = true; q.push (to); d[to] = d[v] + 1; p[to] = v; } } } Если теперь надо восстановить и вывести кратчайший путь до какой-то вершины
if (!used[to]) cout << "No path!"; else { vector<int> path; for (int v=to; v!=-1; v=p[v]) path.push_back (v); reverse (path.begin(), path.end()); cout << "Path: "; for (size_t i=0; i<path.size(); ++i) cout << path[i] + 1 << " "; }
DFS В результате поиска в глубину находится лексикографически первый путь в графе. vector<bool> used; void dfs(int v)
Алгоритм поиска компонент связности в графе
Дан неориентированный граф int n; vector<int> g[MAXN]; bool used[MAXN]; vector<int> comp;
void dfs (int v) (………………………) void find_comps() { for (int i=0; i<n; ++i) used[i] = false; for (int i=0; i<n; ++i) if (! used[i]) { comp.clear();
dfs (i);
cout << "Component:"; for (size_t j=0; j<comp.size(); ++j) cout << ' ' << comp[j]; cout << endl; } }
Поиск мостов Пусть дан неориентированный граф. Мостом называется такое ребро, удаление которого делает граф несвязным (или, точнее, увеличивает число компонент связности). Требуется найти все мосты в заданном графе. Неформально эта задача ставится следующим образом: требуется найти на заданной карте дорог все "важные" дороги, т.е. такие дороги, что удаление любой из них приведёт к исчезновению пути между какой-то парой городов. const int MAXN =...; vector<int> g[MAXN]; bool used[MAXN]; int timer, tin[MAXN], fup[MAXN];
void dfs (int v, int p = -1) { used[v] = true; tin[v] = fup[v] = timer++; for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i]; if (to == p) continue; if (used[to]) fup[v] = min (fup[v], tin[to]); else { dfs (to, v); fup[v] = min (fup[v], fup[to]); if (fup[to] > tin[v]) IS_BRIDGE(v,to); } } }
void find_bridges() { timer = 0; for (int i=0; i<n; ++i) used[i] = false; for (int i=0; i<n; ++i) if (!used[i]) dfs (i); }
Поиск точек сочленения Пусть дан связный неориентированный граф. Точкой сочленения (или точкой артикуляции, англ. "cut vertex" или "articulation point") называется такая вершина, удаление которой делает граф несвязным. vector<int> g[MAXN]; bool used[MAXN]; int timer, tin[MAXN], fup[MAXN];
void dfs (int v, int p = -1) { used[v] = true; tin[v] = fup[v] = timer++; int children = 0; for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i]; if (to == p) continue; if (used[to]) fup[v] = min (fup[v], tin[to]); else { dfs (to, v); fup[v] = min (fup[v], fup[to]); if (fup[to] >= tin[v] && p!= -1) IS_CUTPOINT(v); ++children; } } if (p == -1 && children > 1) IS_CUTPOINT(v); }
int main() { int n; ... чтение n и g...
timer = 0; for (int i=0; i<n; ++i) used[i] = false; dfs (0); } Здесь константе Функция
8)Дейкстра const int INF = 1000000000;
int main() { int n; ... чтение n... vector < vector < pair<int,int> > > g (n); ... чтение графа... int s =...; // стартовая вершина
vector<int> d (n, INF), p (n); d[s] = 0; vector<char> u (n); for (int i=0; i<n; ++i) { int v = -1; for (int j=0; j<n; ++j) if (!u[j] && (v == -1 || d[j] < d[v])) v = j; if (d[v] == INF) break; u[v] = true;
for (size_t j=0; j<g[v].size(); ++j) { int to = g[v][j].first, len = g[v][j].second; if (d[v] + len < d[to]) {
d[to] = d[v] + len; p[to] = v; } } } }
9) Эратосфен int n; vector<char> prime (n+1, true); prime[0] = prime[1] = false; for (int i=2; i<=n; ++i) if (prime[i]) if (i * 1ll * i <= n) for (int j=i*i; j<=n; j+=i) prime[j] = false;
Задача о назначениях Задача имеет две эквивалентные постановки: Дана квадратная матрица A[1..N,1..N]. Нужно выбрать в ней N элементов так, чтобы в каждой строке и столбце был выбран ровно один элемент, а сумма значений этих элементов была наименьшей. Имеется N заказов и N станков. Про каждый заказ известна стоимость его изготовления на каждом станке. На каждом станке можно выполнять только один заказ. Требуется распределить все заказы по станкам так, чтобы минимизировать суммарную стоимость. vector<int> u (n+1), v (m+1), p (m+1), way (m+1); for (int i=1; i<=n; ++i) { p[0] = i; int j0 = 0; vector<int> minv (m+1, INF); vector<char> used (m+1, false); do { used[j0] = true; int i0 = p[j0], delta = INF, j1; for (int j=1; j<=m; ++j) if (!used[j]) { int cur = a[i0][j]-u[i0]-v[j]; if (cur < minv[j]) minv[j] = cur, way[j] = j0; if (minv[j] < delta) delta = minv[j], j1 = j; } for (int j=0; j<=m; ++j) if (used[j]) u[p[j]] += delta, v[j] -= delta; else minv[j] -= delta; j0 = j1; } while (p[j0]!= 0); do { int j1 = way[j0]; p[j0] = p[j1]; j0 = j1; } while (j0); }
Binpow int binpow (int a, int n) { int res = 1; while (n) { if (n & 1) res *= a; a *= a; n >>= 1; } return res; }
Расширенный Евклид В то время как "обычный" алгоритм Евклида просто находит наибольший общий делитель двух чисел
Т.е. он находит коэффициенты, с помощью которых НОД двух чисел выражается через сами эти числа. int gcd (int a, int b, int & x, int & y) { if (a == 0) { x = 0; y = 1; return b; } int x1, y1; int d = gcd (b%a, a, x1, y1); x = y1 - (b / a) * x1; y = x1; return d; }
Длинка Структура данных Хранить длинные числа будем в виде вектора чисел typedef vector<int> lnum; Для повышения эффективности будем работать в системе по основанию миллиард, т.е. каждый элемент вектора const int base = 1000*1000*1000; Цифры будут храниться в векторе в таком порядке, что сначала идут наименее значимые цифры (т.е. единицы, десятки, сотни, и т.д.). Кроме того, все операции будут реализованы таким образом, что после выполнения любой из них лидирующие нули (т.е. лишние нули в начале числа) отсутствуют (разумеется, в предположении, что перед каждой операцией лидирующие нули также отсутствуют). Следует отметить, что в представленной реализации для числа ноль корректно поддерживаются сразу два представления: пустой вектор цифр, и вектор цифр, содержащий единственный элемент — ноль. А)Вывод printf ("%d", a.empty()? 0: a.back()); for (int i=(int)a.size()-2; i>=0; --i) printf ("%09d", a[i]); Б) Чтение for (int i=(int)s.length(); i>0; i-=9) if (i < 9) a.push_back (atoi (s.substr (0, i).c_str())); else a.push_back (atoi (s.substr (i-9, 9).c_str())); В) Сложение int carry = 0; for (size_t i=0; i<max(a.size(),b.size()) || carry; ++i) { if (i == a.size()) a.push_back (0); a[i] += carry + (i < b.size()? b[i]: 0); carry = a[i] >= base; if (carry) a[i] -= base; } Г) Вычитание int carry = 0; for (size_t i=0; i<b.size() || carry; ++i) { a[i] -= carry + (i < b.size()? b[i]: 0); carry = a[i] < 0; if (carry) a[i] += base; } while (a.size() > 1 && a.back() == 0) a.pop_back(); Д) Умножение длинного на короткое int carry = 0; for (size_t i=0; i<a.size() || carry; ++i) { if (i == a.size()) a.push_back (0); long long cur = carry + a[i] * 1ll * b; a[i] = int (cur % base); carry = int (cur / base); } while (a.size() > 1 && a.back() == 0) a.pop_back(); Е) Умножение двух длинных чисел lnum c (a.size()+b.size()); for (size_t i=0; i<a.size(); ++i) for (int j=0, carry=0; j<(int)b.size() || carry; ++j) { long long cur = c[i+j] + a[i] * 1ll * (j < (int)b.size()? b[j]: 0) + carry; c[i+j] = int (cur % base); carry = int (cur / base); } while (c.size() > 1 && c.back() == 0) c.pop_back(); Ж) Деление длинного на короткое
int carry = 0; for (int i=(int)a.size()-1; i>=0; --i) { long long cur = a[i] + carry * 1ll * base; a[i] = int (cur / b); carry = int (cur % b); } while (a.size() > 1 && a.back() == 0) a.pop_back(); carry – остаток
Диофантовы уравнения int gcd (int a, int b, int & x, int & y) { if (a == 0) { x = 0; y = 1; return b; } int x1, y1; int d = gcd (b%a, a, x1, y1); x = y1 - (b / a) * x1; y = x1; return d; }
bool find_any_solution (int a, int b, int c, int & x0, int & y0, int & g) { g = gcd (abs(a), abs(b), x0, y0); if (c % g!= 0) return false; x0 *= c / g; y0 *= c / g; if (a < 0) x0 *= -1; if (b < 0) y0 *= -1; return true; } A,b>0;
Дискретное логарифмирование Задача дискретного логарифмирования заключается в том, чтобы по данным целым
где int solve (int a, int b, int m) { int n = (int) sqrt (m +.0) + 1;
int an = 1; for (int i=0; i<n; ++i) an = (an * a) % m;
map<int,int> vals; for (int i=1, cur=an; i<=n; ++i) { if (!vals.count(cur)) vals[cur] = i; cur = (cur * an) % m; }
for (int i=0, cur=b; i<=n; ++i) { if (vals.count(cur)) { int ans = vals[cur] * n - i; if (ans < m) return ans; } cur = (cur * a) % m; } return -1; }
Максимальный подпалиндром Биномиальные коэффициенты Биномиальным коэффициентом
int C (int n, int k) { double res = 1; for (int i=1; i<=k; ++i) res = res * (n-k+i) / i; return (int) (res + 0.01); }
Числа Каталана Числа Каталана — числовая последовательность, встречающаяся в удивительном числе комбинаторных задач. Первые несколько чисел Каталана
Числа Каталана встречаются в большом количестве задач комбинаторики. Количество корректных скобочных последовательностей, состоящих из Количество корневых бинарных деревьев с Количество способов полностью разделить скобками Количество триангуляций выпуклого Количество способов соединить Количество неизоморфных полных бинарных деревьев с Количество монотонных путей из точки Количество перестановок длины Количество непрерывных разбиений множества из
Количество способов покрыть лесенку Вычисление Имеется две формулы для чисел Каталана: рекуррентная и аналитическая. Поскольку мы считаем, что все приведённые выше задачи эквивалентны, то для доказательства формул мы будем выбирать ту задачу, с помощью которой это сделать проще всего. Рекуррентная формула
Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях. Самой левой открывающей скобке l соответствует определённая закрывающая скобка r, которая разбивает формулу две части, каждая из которых в свою очередь является правильной скобочной последовательностью. Поэтому, если мы обозначим Аналитическая формула
(здесь через Эту формулу проще всего вывести из задачи о монотонных путях. Общее количество монотонных путей в решётке размером
Ожерелья Задача "ожерелья" — это одна из классических комбинаторных задач. Требуется посчитать количество различных ожерелий из Решение Решить эту задачу можно, используя лемму Бернсайда и теорему Пойа. [ Ниже идёт копия текста из этой статьи ] В этой задаче мы можем сразу найти группу инвариантных перестановок. Очевидно, она будет состоять из
Найдём явную формулу для вычисления Подставляя найденные значения в теорему Пойа, получаем решение:
Можно оставить формулу в таком виде, а можно её свернуть ещё больше. Перейдём от суммы по всем
где
Задача о ферзях int SIZE = 0; int board[13][13]; int results_count = 0; void showBoard() { for(int a = 0; a < SIZE; ++a) { for(int b = 0; b < SIZE; ++b) { std::cout << ((board[a][b])? "Q ": ". "); } std::cout << '\n'; } } bool tryQueen(int a, int b) { for(int i = 0; i < a; ++i) { if(board[i][b]) { return false; } }
for(int i = 1; i <= a && b-i >= 0; ++i) { if(board[a-i][b-i]) { return false; } }
for(int i = 1; i <= a && b+i < SIZE; i++) { if(board[a-i][b+i]) { return false; } }
return true; }
void setQueen(int a) { if(a == SIZE) {
results_count++; return; }
for(int i = 0; i < SIZE; ++i) { if(tryQueen(a, i)) { board[a][i] = 1; setQueen(a+1); board[a][i] = 0; } }
return; }
int main() {
std::cin >> SIZE; setQueen(0); std::cout << results_count << std::endl;
return 0; }
36)Ханойские башни void hanoi_towers(int quantity, int from, int to, int buf_peg) { if (quantity!= 0) cout << from << ' ' << to << endl; hanoi_towers(quantity-1, buf_peg, to, from); int main() hanoi_towers(plate_quantity, start_peg, destination_peg, buffer_peg);
Теория Шпрага-Гранди. Ним Введение игру можно полностью описать ориентированным ациклическим графом: вершинами в нём являются состояния игры, а рёбрами — переходы из одного состояния игры в другое в результате хода текущего игрока Поскольку ничейных исходов не бывает, то все состояния игры распадаются на два класса: выигрышные и проигрышные. Выигрышные — это такие состояния, что найдётся ход текущего игрока, который приведёт к неминуемому поражению другого игрока даже при его оптимальной игре. Соответственно, проигрышные состояния — это состояния, из которых все переходы ведут в состояния, приводящие к победе второго игрока, несмотря на "сопротивление" первого игрока. Иными словами, выигрышным будет состояние, из которого есть хотя бы один переход в проигрышное состояние, а проигрышным является состояние, из которого все переходы ведут в выигрышные состояния (или из которого вообще нет переходов). Теорема. Текущий игрок имеет выигрышную стратегию тогда и только тогда, когда XOR-сумма размеров кучек отлична от нуля. В противном случае текущий игрок находится в проигрышном состоянии. (XOR-суммой чисел Теорема Шпрага-Гранди об эквивалентности любой игры ниму Теорема Шпрага-Гранди. Рассмотрим любое состояние Более того, это число
где функция Таким образом, мы можем, стартуя от вершин без исходящих рёбер, постепенно посчитать значения Шпрага-Гранди для всех состояний нашей игры. Если значение Шпрага-Гранди какого-либо состояния равно нулю, то это состояние проигрышно, иначе — выигрышно. Применение теоремы Шпрага-Гранди Функция, которая каждому состоянию игры ставит в соответствие ним-число, называется функцией Шпрага-Гранди. Итак, чтобы посчитать функцию Шпрага-Гранди для текущего состояния некоторой игры, нужно: Выписать все возможные переходы из текущего состояния. Каждый такой переход может вести либо в одну игру, либо в сумму независимых игр. В первом случае — просто посчитаем функцию Гранди рекурсивно для этого нового состояния. Во втором случае, когда переход из текущего состояния приводит в сумму нескольких независимых игр — рекурсивно посчитаем для каждой из этих игр функцию Гранди, а затем скажем, что функция Гранди суммы игр равна XOR-сумме значений этих игр. После того, как мы посчитали функцию Гранди для каждого возможного перехода — считаем Если полученное значение Гранди равно нулю, то текущее состояние проигрышно, иначе — выигрышно. Таким образом, по сравнению с теоремой Шпрага-Гранди здесь мы учитываем то, что в игре могут быть переходы из отдельных состояний в суммы нескольких игр. Чтобы работать с суммами игр, мы сначала заменяем каждую игру её значением Гранди, т.е. одной ним-кучкой некоторого размера. После этого мы приходим к сумме нескольких ним-кучек, т.е. к обычному ниму, ответ для которого, согласно теореме Бутона — XOR-сумма размеров кучек. Закономерности в значениях Шпрага-Гранди "Крестики-крестики" Условие. Рассмотрим клетчатую полоску размера Решение. Когда игрок ставит крестик в какую-либо клетку, можно считать, что вся полоска распадается на две независимые половинки: слева от крестика и справа от него. При этом сама клетка с крестиком, а также её левый и правый сосед уничтожаются — т.к. в них больше ничего нельзя будет поставить. Следовательно, если мы занумеруем клетки полоски от Таким образом, функция Гранди
Т.е. Итак, мы получили решение этой задачи за На самом деле, посчитав на компьютере таблицу значений для первой сотни значений "Крестики-крестики — 2" Условие. Снова игра ведётся на полоске Решение. Заметим, что если Тогда решение получается практически аналогичным предыдущей задаче, только теперь крестик удаляет у каждой половинки не по одной, а сразу по две клетки. "Пешки" Условие. Есть поле Решение. Проследим, что происходит, когда одна пешка сделает ход вперёд. Следующим ходом противник будет обязан съесть её, затем мы будем обязаны съесть пешку противника, затем снова он съест, и, наконец, наша пешка съест вражескую пешку и останется, "упёршись" в пешку противника. Таким образом, если мы в самом начале пошли пешкой в колонке "Lasker's nim" Условие. Имеется Решение. Записывая оба вида переходов, легко получить функцию Шпрага-Гранди как:
Однако можно построить таблицу значений для малых
Здесь видно, что "The game of Kayles" Условие. Есть Решение. И когда игрок выбивает одну кеглю, и когда он выбивает две — игра распадается на сумму двух независимых игр. Нетрудно получить такое выражение для функции Шпрага-Гранди:
Посчитаем для него таблицу для нескольких первых десятков элементов:
Можно заметить, что, начиная с некоторого момента, последовательность становится периодичной с периодом Grundy's game Условие. Есть Решение. Если Для одной кучки эта функция строится также легко, достаточно просмотреть все возможные переходы:
Чем эта игра интересна — тем, что до сих пор для неё не найдено общей закономерности. Несмотря на предположения, что последовательность "Лестничный ним" Условие. Есть лестница с Решение. Если попытаться свести эту задачу к ниму "в лоб", то получится, что ход у нас — это уменьшение одной кучки на сколько-то, и одновременное увеличение другой кучки на столько же. В итоге мы получаем модификацию нима, решить которую весьма сложно. Поступим по-другому: рассмотрим только ступеньки с чётными номерами:
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.172.5 (0.011 с.) |

 с
с 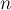 вершинами. Требуется найти значения всех величин
вершинами. Требуется найти значения всех величин  — длины кратчайшего пути из вершины
— длины кратчайшего пути из вершины 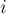 в вершину
в вершину  .
. , где
, где  — число рёбер.
— число рёбер. , это можно сделать следующим образом:
, это можно сделать следующим образом: должно быть задано значение, равное максимально возможному числу вершин во входном графе.
должно быть задано значение, равное максимально возможному числу вершин во входном графе. в коде — это некая функция, которая будет реагировать на то, что вершина
в коде — это некая функция, которая будет реагировать на то, что вершина  является точкой сочленения, например, выводить эту вершины на экран (надо учитывать, что для одной и той же вершины эта функция может быть вызвана несколько раз).
является точкой сочленения, например, выводить эту вершины на экран (надо учитывать, что для одной и той же вершины эта функция может быть вызвана несколько раз). и
и  , расширенный алгоритм Евклида находит помимо НОД также коэффициенты
, расширенный алгоритм Евклида находит помимо НОД также коэффициенты  и
и  такие, что:
такие, что:
 , где каждый элемент — это одна цифра числа.
, где каждый элемент — это одна цифра числа. содержит не одну, а сразу
содержит не одну, а сразу  цифр:
цифр:
 называется количество способов выбрать набор
называется количество способов выбрать набор  предметов из
предметов из  (начиная с нулевого):
(начиная с нулевого):
 листьями (вершины не пронумерованы).
листьями (вершины не пронумерованы). -угольника (т.е. количество разбиений многоугольника непересекающимися диагоналями на треугольники).
-угольника (т.е. количество разбиений многоугольника непересекающимися диагоналями на треугольники). точек на окружности
точек на окружности 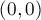 в точку
в точку  в квадратной решётке размером
в квадратной решётке размером  , не поднимающихся над главной диагональю.
, не поднимающихся над главной диагональю. , что
, что  ).
). с помощью
с помощью 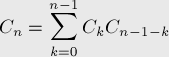
 , то для любого фиксированного
, то для любого фиксированного  будет ровно
будет ровно  способов. Суммируя это по всем допустимым
способов. Суммируя это по всем допустимым 
 . Теперь посчитаем количество монотонных путей, пересекающих диагональ. Рассмотрим какой-либо из таких путей, и найдём первое ребро, которое стоит выше диагонали. Отразим относительно диагонали весь путь, идущий после этого ребра. В результате получим монотонный путь в решётке
. Теперь посчитаем количество монотонных путей, пересекающих диагональ. Рассмотрим какой-либо из таких путей, и найдём первое ребро, которое стоит выше диагонали. Отразим относительно диагонали весь путь, идущий после этого ребра. В результате получим монотонный путь в решётке  . Но, с другой стороны, любой монотонный путь в решётке
. Но, с другой стороны, любой монотонный путь в решётке  . В результате получаем формулу:
. В результате получаем формулу:





 . Во-первых, заметим, что перестановки имеют такой вид, что в
. Во-первых, заметим, что перестановки имеют такой вид, что в 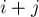 (взятое по модулю
(взятое по модулю  ,
,  ,
,  , и т.д., пока не придём в число
, и т.д., пока не придём в число  ; для остальных элементов выполняются похожие утверждения. Отсюда можно понять, что все циклы имеют одинаковую длину, равную
; для остальных элементов выполняются похожие утверждения. Отсюда можно понять, что все циклы имеют одинаковую длину, равную  , т.е.
, т.е.  ("gcd" — наибольший общий делитель, "lcm" — наименьшее общее кратное). Тогда количество циклов в
("gcd" — наибольший общий делитель, "lcm" — наименьшее общее кратное). Тогда количество циклов в  .
.
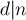 его слагаемое
его слагаемое  учтётся несколько раз, т.е. сумму можно представить в таком виде:
учтётся несколько раз, т.е. сумму можно представить в таком виде: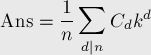
 — это количество таких чисел
— это количество таких чисел 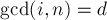 . Найдём явное выражение для этого количества. Любое такое число
. Найдём явное выражение для этого количества. Любое такое число  , где
, где  (иначе было бы
(иначе было бы  ). Вспоминая функцию Эйлера, мы находим, что количество таких
). Вспоминая функцию Эйлера, мы находим, что количество таких  . Таким образом,
. Таким образом,  , и окончательно получаем формулу:
, и окончательно получаем формулу:
 называется выражение
называется выражение  , где
, где  — операция побитового исключающего или)
— операция побитового исключающего или)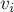
 (где
(где  ). Утверждается, что состоянию
). Утверждается, что состоянию  по каждому переходу
по каждому переходу  , и тогда выполняется:
, и тогда выполняется: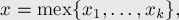
 от множества чисел возвращает наименьшее неотрицательное число, не встречающееся в этом множестве (название "mex" — это сокращение от "minimum excludant").
от множества чисел возвращает наименьшее неотрицательное число, не встречающееся в этом множестве (название "mex" — это сокращение от "minimum excludant"). клеток. За один ход игроку надо поставить один крестик, но при этом запрещено ставить два крестика рядом (в соседние клетки). Проигрывает тот, кто не может сделать ход. Сказать, кто выиграет при оптимальной игре.
клеток. За один ход игроку надо поставить один крестик, но при этом запрещено ставить два крестика рядом (в соседние клетки). Проигрывает тот, кто не может сделать ход. Сказать, кто выиграет при оптимальной игре. до
до  , полоска распадётся на две полоски длины
, полоска распадётся на две полоски длины  и
и  , т.е. мы переходим в сумму двух игр
, т.е. мы переходим в сумму двух игр  .
.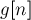 имеет вид (для
имеет вид (для 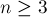 ):
):
 , а также всевозможных значений выражения
, а также всевозможных значений выражения  .
.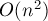 .
. , последовательность
, последовательность  . Эта закономерность сохраняется и дальше
. Эта закономерность сохраняется и дальше и мы оставили после своего хода два крестика рядом или через один пробел, то противник следующим ходом выиграет. Следовательно, если один игрок поставил где-то крестик, то другому игроку невыгодно ставить крестик в соседние с ним клетки, а также в соседние с соседними (т.е. на расстоянии
и мы оставили после своего хода два крестика рядом или через один пробел, то противник следующим ходом выиграет. Следовательно, если один игрок поставил где-то крестик, то другому игроку невыгодно ставить крестик в соседние с ним клетки, а также в соседние с соседними (т.е. на расстоянии  ставить невыгодно, это приведёт к поражению).
ставить невыгодно, это приведёт к поражению). , на котором в первом и третьем ряду стоят по
, на котором в первом и третьем ряду стоят по  доски фактически уничтожатся, и мы перейдём к сумме игр размера
доски фактически уничтожатся, и мы перейдём к сумме игр размера  и
и  приводят нас просто к доске размера
приводят нас просто к доске размера 

 для чисел, равных
для чисел, равных  , и
, и  для чисел, равных
для чисел, равных  и
и  по модулю
по модулю 

 . В дальнейшем эта периодичность также не нарушится.
. В дальнейшем эта периодичность также не нарушится. , то все эти несколько кучек, очевидно, — независимые игры. Следовательно, наша задача — научиться искать функцию Шпрага-Гранди для одной кучки, а ответ для нескольких кучек будет получаться как их XOR-сумма.
, то все эти несколько кучек, очевидно, — независимые игры. Следовательно, наша задача — научиться искать функцию Шпрага-Гранди для одной кучки, а ответ для нескольких кучек будет получаться как их XOR-сумма.
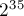 , и периодов в этой области обнаружено не было.
, и периодов в этой области обнаружено не было.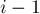 -ую ступеньку. Проигрывает тот, кто не может сделать хода.
-ую ступеньку. Проигрывает тот, кто не может сделать хода. . Посмотрим, как будет меняться э
. Посмотрим, как будет меняться э 


