
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм Куна нахождения наибольшего паросочетания в двудольном графеСодержание книги
Поиск на нашем сайте
Дан двудольный граф Теорема Бержа Формулировка. Паросочетание является максимальным тогда и только тогда, когда не существует увеличивающих относительно него цепей. int n, k; vector < vector<int> > g; vector<int> mt; vector<char> used;
bool try_kuhn (int v) { if (used[v]) return false; used[v] = true; for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i]; if (mt[to] == -1 || try_kuhn (mt[to])) { mt[to] = v; return true; } } return false; }
int main() { ... чтение графа...
mt.assign (k, -1); vector<char> used1 (n); for (int i=0; i<n; ++i) for (size_t j=0; j<g[i].size(); ++j) if (mt[g[i][j]] == -1) { mt[g[i][j]] = i; used1[i] = true; break; } for (int i=0; i<n; ++i) { if (used1[i]) continue; used.assign (n, false); try_kuhn (i); }
for (int i=0; i<k; ++i) if (mt[i]!= -1) printf ("%d %d\n", mt[i]+1, i+1); }
12)Эйлер int phi (int n) { int result = n; for (int i=2; i*i<=n; ++i) if (n % i == 0) { while (n % i == 0) n /= i; result -= result / i; } if (n > 1) result -= result / n; return result; }
Binpow int binpow (int a, int n) { int res = 1; while (n) { if (n & 1) res *= a; a *= a; n >>= 1; } return res; }
Расширенный Евклид В то время как "обычный" алгоритм Евклида просто находит наибольший общий делитель двух чисел
Т.е. он находит коэффициенты, с помощью которых НОД двух чисел выражается через сами эти числа. int gcd (int a, int b, int & x, int & y) { if (a == 0) { x = 0; y = 1; return b; } int x1, y1; int d = gcd (b%a, a, x1, y1); x = y1 - (b / a) * x1; y = x1; return d; }
Длинка Структура данных Хранить длинные числа будем в виде вектора чисел typedef vector<int> lnum; Для повышения эффективности будем работать в системе по основанию миллиард, т.е. каждый элемент вектора const int base = 1000*1000*1000; Цифры будут храниться в векторе в таком порядке, что сначала идут наименее значимые цифры (т.е. единицы, десятки, сотни, и т.д.). Кроме того, все операции будут реализованы таким образом, что после выполнения любой из них лидирующие нули (т.е. лишние нули в начале числа) отсутствуют (разумеется, в предположении, что перед каждой операцией лидирующие нули также отсутствуют). Следует отметить, что в представленной реализации для числа ноль корректно поддерживаются сразу два представления: пустой вектор цифр, и вектор цифр, содержащий единственный элемент — ноль. А)Вывод printf ("%d", a.empty()? 0: a.back()); for (int i=(int)a.size()-2; i>=0; --i) printf ("%09d", a[i]); Б) Чтение for (int i=(int)s.length(); i>0; i-=9) if (i < 9) a.push_back (atoi (s.substr (0, i).c_str())); else a.push_back (atoi (s.substr (i-9, 9).c_str())); В) Сложение int carry = 0; for (size_t i=0; i<max(a.size(),b.size()) || carry; ++i) { if (i == a.size()) a.push_back (0); a[i] += carry + (i < b.size()? b[i]: 0); carry = a[i] >= base; if (carry) a[i] -= base; } Г) Вычитание int carry = 0; for (size_t i=0; i<b.size() || carry; ++i) { a[i] -= carry + (i < b.size()? b[i]: 0); carry = a[i] < 0; if (carry) a[i] += base; } while (a.size() > 1 && a.back() == 0) a.pop_back(); Д) Умножение длинного на короткое int carry = 0; for (size_t i=0; i<a.size() || carry; ++i) { if (i == a.size()) a.push_back (0); long long cur = carry + a[i] * 1ll * b; a[i] = int (cur % base); carry = int (cur / base); } while (a.size() > 1 && a.back() == 0) a.pop_back(); Е) Умножение двух длинных чисел lnum c (a.size()+b.size()); for (size_t i=0; i<a.size(); ++i) for (int j=0, carry=0; j<(int)b.size() || carry; ++j) { long long cur = c[i+j] + a[i] * 1ll * (j < (int)b.size()? b[j]: 0) + carry; c[i+j] = int (cur % base); carry = int (cur / base); } while (c.size() > 1 && c.back() == 0) c.pop_back(); Ж) Деление длинного на короткое int carry = 0; for (int i=(int)a.size()-1; i>=0; --i) { long long cur = a[i] + carry * 1ll * base; a[i] = int (cur / b); carry = int (cur % b); } while (a.size() > 1 && a.back() == 0) a.pop_back(); carry – остаток
Диофантовы уравнения int gcd (int a, int b, int & x, int & y) { if (a == 0) { x = 0; y = 1; return b; } int x1, y1; int d = gcd (b%a, a, x1, y1); x = y1 - (b / a) * x1; y = x1; return d; }
bool find_any_solution (int a, int b, int c, int & x0, int & y0, int & g) { g = gcd (abs(a), abs(b), x0, y0); if (c % g!= 0) return false; x0 *= c / g; y0 *= c / g; if (a < 0) x0 *= -1; if (b < 0) y0 *= -1; return true; } A,b>0;
Нахождение степени делителя факториала Даны два числа: int fact_pow (int n, int k) { int res = 0; while (n) { n /= k; res += n; } return res; }
Дискретное логарифмирование Задача дискретного логарифмирования заключается в том, чтобы по данным целым
где int solve (int a, int b, int m) { int n = (int) sqrt (m +.0) + 1;
int an = 1; for (int i=0; i<n; ++i) an = (an * a) % m;
map<int,int> vals; for (int i=1, cur=an; i<=n; ++i) { if (!vals.count(cur)) vals[cur] = i; cur = (cur * an) % m; }
for (int i=0, cur=b; i<=n; ++i) { if (vals.count(cur)) { int ans = vals[cur] * n - i; if (ans < m) return ans; } cur = (cur * a) % m; } return -1; }
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 866; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 , содержащий
, содержащий 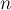 вершин и
вершин и  рёбер. Требуется найти наибольшее паросочетание, т.е. выбрать как можно больше рёбер, чтобы ни одно выбранное ребро не имело общей вершины ни с каким другим выбранным ребром.
рёбер. Требуется найти наибольшее паросочетание, т.е. выбрать как можно больше рёбер, чтобы ни одно выбранное ребро не имело общей вершины ни с каким другим выбранным ребром. и
и  , расширенный алгоритм Евклида находит помимо НОД также коэффициенты
, расширенный алгоритм Евклида находит помимо НОД также коэффициенты  и
и  такие, что:
такие, что:
 , где каждый элемент — это одна цифра числа.
, где каждый элемент — это одна цифра числа. содержит не одну, а сразу
содержит не одну, а сразу  цифр:
цифр: . Требуется посчитать, с какой степенью делитель
. Требуется посчитать, с какой степенью делитель 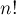 , т.е. найти наибольшее
, т.е. найти наибольшее 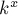 .
.



