
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение площади простого многоугольникаСодержание книги Поиск на нашем сайте
double sq (const vector<point> & fig) { double res = 0; for (unsigned i=0; i<fig.size(); i++) { point p1 = i? fig[i-1]: fig.back(), p2 = fig[i]; res += (p1.x - p2.x) * (p1.y + p2.y); } return fabs (res) / 2; }
20) Теорема Пика.
Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами (в декартовой системе координат) Пусть дан некоторый решётчатый многоугольник, с ненулевой площадью. Обозначим его площадь через Тогда справедливо соотношение, называемое формулой Пика:
Пересечение окружности и прямой Дана окружность (координатами своего центра и радиусом) и прямая (своим уравнением). Требуется найти точки их пересечения (одна, две, либо ни одной). Сначала найдём ближайшую к центру точку прямой - точку с некоторыми координатами (x0,y0). Во-первых, эта точка должна находиться на таком расстоянии от начала координат: |C| ---------- sqrt(A2+B2) _________________________
A C x0 = - ----- A2+B2
B C y0 = - ----- A2+B2 _____________________________________ C2 d = sqrt (r2 - -----) A2+B2 _____________________________________ d2 mult = sqrt (-----) A2+B2
ax = x0 + B mult ay = y0 - A mult bx = x0 - B mult by = y0 + A mult
double r, a, b, c; // входные данные
double x0 = -a*c/(a*a+b*b), y0 = -b*c/(a*a+b*b); if (c*c > r*r*(a*a+b*b)+EPS) puts ("no points"); else if (abs (c*c - r*r*(a*a+b*b)) < EPS) { puts ("1 point"); cout << x0 << ' ' << y0 << '\n'; } else { double d = r*r - c*c/(a*a+b*b); double mult = sqrt (d / (a*a+b*b)); double ax,ay,bx,by; ax = x0 + b * mult; bx = x0 - b * mult; ay = y0 - a * mult; by = y0 + a * mult; puts ("2 points"); cout << ax << ' ' << ay << '\n' << bx << ' ' << by << '\n'; }
Поиск общих касательных к двум окружностям Даны две окружности. Требуется найти все их общие касательные, т.е. все такие прямые, которые касаются обеих окружностей одновременно. Описанный алгоритм будет работать также в случае, когда одна (или обе) окружности вырождаются в точки. Таким образом, этот алгоритм можно использовать также для нахождения касательных к окружности, проходящих через заданную точку. struct pt { double x, y;
pt operator- (pt p) { pt res = { x-p.x, y-p.y }; return res; } };
struct circle: pt { double r; };
struct line { double a, b, c; };
const double EPS = 1E-9;
double sqr (double a) { return a * a; }
void tangents (pt c, double r1, double r2, vector<line> & ans) { double r = r2 - r1; double z = sqr(c.x) + sqr(c.y); double d = z - sqr(r); if (d < -EPS) return; d = sqrt (abs (d)); line l; l.a = (c.x * r + c.y * d) / z; l.b = (c.y * r - c.x * d) / z; l.c = r1; ans.push_back (l); }
vector<line> tangents (circle a, circle b) { vector<line> ans; for (int i=-1; i<=1; i+=2) for (int j=-1; j<=1; j+=2) tangents (b-a, a.r*i, b.r*j, ans); for (size_t i=0; i<ans.size(); ++i) ans[i].c -= ans[i].a * a.x + ans[i].b * a.y; return ans; }
Z-функция строки и её вычисление Пусть дана строка Иными словами, vector<int> z_function (string s) { int n = (int) s.length(); vector<int> z (n); for (int i=1, l=0, r=0; i<n; ++i) { if (i <= r) z[i] = min (r-i+1, z[i-l]); while (i+z[i] < n && s[z[i]] == s[i+z[i]]) ++z[i]; if (i+z[i]-1 > r) l = i, r = i+z[i]-1; } return z; }
Префикс-функция. Алгоритм Кнута-Морриса-Пратта vector<int> prefix_function (string s) { int n = (int) s.length(); vector<int> pi (n); for (int i=1; i<n; ++i) { int j = pi[i-1]; while (j > 0 && s[i]!= s[j]) j = pi[j-1]; if (s[i] == s[j]) ++j; pi[i] = j; } return pi; }
КМП /* Preprocessing */
void PRE_KMP(char *x, int m, int kmp_next[]) { int i, j;
i=0; j=kmp_next[0]=-1; while (i < m) { while (j > -1 && x[ i ]!= x[ j ]) j=kmp_next[ j ]; i++; j++; if (x[ i ] == x[ j ]) kmp_next[i]=kmp_next[j]; else kmp_next[ i ] = j; } }
void KMP(char *x, char *y, int n, int m) { int i, j, kmp_next[XSIZE];
/* Preprocessing */ PRE_KMP(x, m, kmp_next);
/* Searching */
i=j=0; while (i < n) { while (j > -1 && x[ j ]!= y[ i ]) j = kmp_next[ j ]; i++; j++; if (j >= m) { OUTPUT(i - j); j = kmp_next[ j ]; } } }
Нахождение всех подпалиндромов bool is_poly(const string& S, int i, int j) { if (i == j) return false; while (i < j) { ++i; --j; if (S[i]!= S[j]) return false; } return true; } //* int poly (const string &S) { int count = 0; int size = S.size(); if (1 == size) return 1; int j = 0; for(int i = 0; i < size-1;++i) { char begin = S[i]; j = S.find_last_of(begin, size-begin-1); while(-1!= j) { bool is_p = is_poly(S, i, j); if (is_p) { ++count; } j = S.find_last_of(begin,j-1); if (i >= j) break; } } return count; } Максимальный подпалиндром
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.247.221 (0.009 с.) |

 ; количество точек с целочисленными координатами, лежащих строго внутри многоугольника — через
; количество точек с целочисленными координатами, лежащих строго внутри многоугольника — через 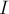 ; количество точек с целочисленными координатами, лежащих на сторонах многоугольника — через
; количество точек с целочисленными координатами, лежащих на сторонах многоугольника — через 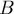 .
.
 длины
длины 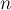 . Тогда Z-функция ("зет-функция") от этой строки — это массив длины
. Тогда Z-функция ("зет-функция") от этой строки — это массив длины 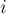 -ый элемент которого равен наибольшему числу символов, начиная с позиции
-ый элемент которого равен наибольшему числу символов, начиная с позиции  — это наибольший общий префикс строки
— это наибольший общий префикс строки 


