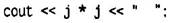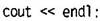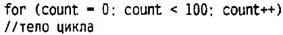Несколько операторов в теле цикла

Массивы

Начнем с классического понятия в сильно типизированных языках (например, в языке Паскаль). Тип массива в таких языках определяется на основе двух вспомогательных типов: типа элементов массива (базового типа) и типа индекса массива. В языке Паскаль определение типа массива выглядит следующим образом: type T =array [ I ] of Т0, где Т0 - базовый тип, а I - тип индекса. Т0 может быть любым встроенным или ранее определенным типом. Тип индекса I должен состоять из конечного числа перечисляемых значений, т.е. быть уточненным, перечисляемым, символьным или булевским типом. В языках линии Паскаль допускается и неявное определение уточненного типа массива. Например, допустимы следующие определения типа массива: type T =array [1..6] of integer или type T = array [' a..' e '] of real.

Если мощность множества значений типа индекса есть n, то значение типа массива - это регулярная структура, включающая п элементов базового типа. Соответствующим образом устроены и переменные типа массива. Для любого сконструированного типа массива предопределены две операции - операция конструирования значения типа массива и операция выборки элемента массива. Если х -переменная типа массива Т, a i - значение соответствующего типа индекса, то для конструирования значения используется языковое средство х: = Т (c 1, с2,..., с n), где c 1, с2,..., сп -значения базового типа. Для выборки элемента массива используется конструкция x [ i ], значением которой является значение i -тогоэлемента массива (вместо i в квадратных скобках может содержаться любое допустимое выражение, значение которого принадлежит множеству значений типа индекса). Эта же конструкция может использоваться в левой части оператора присваивания, т.е. элементы массива могут изменяться индивидуально. Кроме того, при подобной строгой типизации массивов допустимы присваивания значений переменных типа массива, функции, возвращающие значение типа массива и т.п.

Базовым типом типа массива может быть любой встроенный или определенный тип, в том числе и тип массива. В последнем случае говорят о многомерных массивах или матрицах. Для работы с многомерными массивами в языках используют сокращенную запись. Например. вместо определения type T =array [1..10] of array [1..5] of real можно написать type T = array [1..10], [1..5] of real, а если x - переменная такого типа Т, то для выборки скалярного элемента вместо x [ i ][ j ] можно написать x [ i, j ].

В сильно типизированных языках для любого значения типа массива известно число элементов базового типа. Поэтому в принципе всегда возможен контроль значения индекса, хотя на практике такой контроль обычно отменяется при использовании программы в производственном режиме.

Для иллюстрации приемов работы с массивами в слабо типизированных языках используем язык Си. В этом языке нет средств определения типов массива, хотя имеется возможность определения «массивных переменных». Число элементов в массивной переменной определяется либо явно, либо с помощью задания списка инициализирующих значений базового типа. Например, массивную переменную с четырьмя элементами целого типа можно определить как int х [4](неинициализированный вариант) или как int х [] = {0, 2,8, 22} (инициализированная массивная переменная). Доступ к элементам массивной переменной производится с помощью конструкции выбора, по виду аналогичной соответствующей конструкции в сильно типизированных языках x [ i ], где i -выражение, принимающее целое значение (мы специально отметили внешний характер аналогии, поскольку в отличие от языка Паскаль в языке Си зафиксирована интерпретация операции выбора на основе более примитивных операций адресной арифметики). Однако, в реализациях языка Си в принципе невозможен контроль выхода значения индекса за пределы массива. Кроме того, по аналогичным причинам невозможно присваивание значений массивных переменных и не допускаются функции, вырабатывающие «массивные значения».

Записи

Типы массивов позволяют работать с регулярными структурами данных, каждый элемент которых относится к одному и тому же базовому типу. Существует другая разновидность составных конструируемых типов данных, которые позволяют определять и использовать нерегулярные структуры данных, элементы которых могут относиться к разным встроенным или явно определенным типам данных. Собирательно типы этой разновидности называются типами записи или структурными типами.

К счастью, общее понятие типа записи практически одинаково в сильно и слабо типизированных языках. Идея состоит в том, что в определении структурного тип; перечисляются имена полей записи, и для каждого поля указывается его тип данных. После этого можно определять переменные вновь сконструированного типа и производить доступ к полям переменных. На языке Модула-2 определение структурного типа «комплексные числа» могло бы выглядеть следующим образом:

type complex = record re: real;

im: real

end

Множества

Еще одной разновидностью конструируемых типов являются типы множеств. Такие типы поддерживаются только в развитых сильно типизированных языках. В языке Паскаль тип множества определяется конструкцией type Т =set of T 0, где Т0 -встроенный или ранее определенный тип данных (базовый тип). Значениями переменных типа Т являются множества элементов типа Т0 (в частности, пустые множества).

Для любого типа множества определены следующие операции: «?» - пересечение множеств, «+» - объединение множеств, «–» - вычитание множеств и «in» - проверка принадлежности к множеству элемента базового типа.

С использованием механизма множеств можно писать лаконичные и красивые программы, но нужно отдавать себе отчет в том, что для эффективной реализации множеств требуются серьезные ограничения их мощности. Обычно в реализациях языков допускаются множества, мощность базового типа которых не превосходит длину машинного слова. Это связано с тем, что перечисленные выше операции допускают эффективную реализацию только а том случае, когда значение множества представляется битовой шкалой, длина которой равна мощности базового типа. «1» означает, что соответствующий элемент базового типа входит в множество, «0» - не входит. Чтобы для выполнения операций над множествами можно было прямо использовать машинные команды, нужно ограничить длину шкалы машинным словом.

 

· ТЕМА 11. ЦИКЛЫ

Действие циклов заключается в последовательном повторении определенной части вашей программы некоторое количество раз. Повторение продолжается до тех пор, пока выполняется соответствующее условие. Когда значение выражения, задающего условие, становится ложным, выполнение цикла прекращается, а управление передается оператору, следующему непосредственно за циклом.

В C++ существует 3 типа циклов: for, while и do.

Цикл for

Большинство изучающих язык C++ считают цикл for самым легким для понимания. Все элементы, контролирующие его выполнение, собраны в одном месте, в то время как в циклах других типов они разбросаны внутри цикла, что зачастую делает логику его работы трудной для понимания.

Цикл for организует выполнение фрагмента программы фиксированное число раз. Как правило (хотя и не всегда), этот тип цикла используется тогда, когда число раз, за которое должно повториться исполнение кода, известно заранее.

В примере FORDEMO, приведенном ниже, выводятся на экран квадраты целых чисел от 0 до 14:

Результат работы программы выглядит так:

0 1 4 9 16 25 36 49 64 81 100 121 144 169 196

Каким образом работает эта программа? Оператор for управляет циклом. Он состоит из ключевого слова for, за которым следуют круглые скобки, содержащие три выражения, разделенные точками с запятой:

Первое из трех выражений называют инициализирующим, второе - условием проверки, а третье - инкрементирующим, как показано на рис. 3.1.

Рис. 3.1. Синтаксис цикла for

Эти три выражения, как правило (но не всегда), содержат одну переменную, которую обычно называют счетчиком цикла. В примере FORDEMO счетчиком цикла является переменная j. Она определяется до того, как начнет исполняться тело цикла.

Под телом цикла понимается та часть кода, которая периодически исполняется в цикле. В нашем примере тело цикла состоит из единственного оператора

Данный оператор печатает квадрат значения переменной j и два пробела после него. Квадрат находится как произведения переменной j самой на себя. Во время исполнения цикла переменная j принимает значения 0, 1, 2, 3 и т.д. до 14, а выводимые значения квадратов соответственно 0, 1, 4, 9,..., 196.

Обратите внимание на то, что после оператора for отсутствует точка с запятой (;). Это объясняется тем, что на самом деле оператор for вместе с телом цикла представляют из себя один оператор. Это очень важная деталь, поскольку если поставить после оператора for точку с запятой, то компилятор воспримет это как отсутствие тела цикла, и результат работы программы будет отличаться от задуманного.

Рассмотрим, каким образом три выражения, стоящие в круглых скобках оператора for, влияют на работу цикла.

Инициализирующее выражение

Инициализирующее выражение вычисляется только один раз - в начале выполнения цикла. Вычисленное значение инициализирует счетчик цикла. В примере FORDEMO переменная j получает значение 0.

Условие выполнения цикла

Как правило, условие выполнения цикла содержит в себе операцию отношения. Условие проверяется каждый раз перед исполнением тела цикла и определяет, нужно ли исполнять цикл еще раз или нет. Если условие выполняется, то есть соответствующее выражение истинно, то цикл исполняется еще раз. В противном случае управление передается тому оператору, который следует за циклом. В программе FORDEMO после завершения цикла управление передается оператору

Инкрементирующее выражение

Инкрементирующее выражение предназначено для изменения значения счетчика цикла. Часто такое изменение сводится к инкрементированию счетчика. Модификация счетчика происходит после того, как тело цикла полностью выполнилось. В нашем примере увеличение j на единицу происходит каждый раз после завершения тела цикла.

Блок-схема, иллюстрирующая исполнение цикла for, приведена на рис. 3.2.

Рис. 3.2. Исполнение цикла for

Число выполнений цикла

В примере FORDEMO цикл выполняется 15 раз. В первый раз он выполняется при нулевом значении j. Последнее исполнение цикла произойдет при j = 14, поскольку условием выполнения цикла служит j < 15. Когда j принимает значение, равное 15, выполнение цикла прекращается. Как правило, подобную схему исполнения применяют в том случае, когда необходимые действия нужно выполнить фиксированное количество раз. Присваивая счетчику начальное значение, равное 0, в качестве условия продолжения цикла ставят сравнение счетчика с желаемым числом выполнений и увеличивают счетчик на единицу каждый раз, когда исполнение тела цикла завершается. Например, цикл

будет выполнен 100 раз, а счетчик count будет принимать значения от 0 до 99.

Варианты цикла for

Инкрементирующий оператор не обязательно должен производить операцию инкрементирования счетчика цикла; вместо инкрементирования может использоваться любая другая операция, В следующем примере под названием FACTOR в операторе цикла используется декрементирование счетчика цикла, Программа запрашивает значение у пользователя, а затем подсчитывает факториал этого числа (факториал числа представляет из себя произведение всех целых положительных чисел, не превышающих данное число. Например, факториал числа 5 равен 1*2*3*4*5 = 120).

В этом примере инициализирующий оператор присваивает переменной j значение, вводимое пользователем. Условием продолжения цикла является положительность значения j. Инкрементирующее выражение после каждой итерации уменьшает значение j на единицу.

Мы использовали тип unsigned long для переменной, хранящей значение факториала, потому, что даже для небольших чисел значения их факториалов очень велико. В 32-битных системах размеры типов int и long совпадают, но в 16-битных системах размер типа long больше. Следующий результат работы программы показывает, насколько велико может быть значение факториала даже для небольшого числа:

Самое большое число, которое можно использовать для ввода в этой программе, равно 12. Для чисел больше 12 результат работы программы будет неверен, поскольку произойдет переполнение.

Цикл while

Цикл for выполняет последовательность действий определенное количество раз. А как поступить в том случае, если заранее не известно, сколько раз понадобится выполнить цикл? Для этого разработан другой вид цикла - while.

В следующем примере под названием ENDON 0 пользователю предлагают ввести серию значений. В том случае, когда вводимое значение оказывается равным нулю, происходит выход из цикла. Очевидно, что в этой ситуации заранее невозможно узнать, сколько ненулевых значений введет пользователь.

Далее мы приведем возможный пример работы программы. Пользователь вводит значения, а программа отображает эти значения до тех пор, пока пользователь не введет ноль, после чего программа завершается.

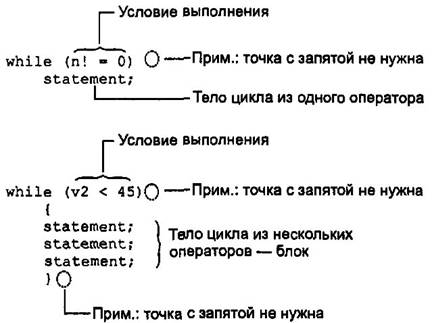
Внешне цикл while напоминает упрощенный вариант цикла for. Он содержит условие для продолжения цикла, но не содержит ни инициализирующих, ни инкрементирующих выражений. Синтаксис цикла while показан на рис. 3.3.

Рис. 3.3. Синтаксис цикла while

До тех пор пока условие продолжения цикла выполняется, исполнение тела цикла продолжается. В примере ENDON 0 значение выражения

истинно до тех пор, пока пользователь не введет ноль.

На рис. 3.4 показан механизм работы цикла while. На самом деле он не так прост, как кажется вначале. Несмотря на отсутствие инициализирующего оператора, нужно инициализировать переменную цикла до начала исполнения тела цикла. Тело цикла должно содержать оператор, изменяющий значение переменной цикла, иначе цикл будет бесконечным. Таким оператором в цикле из примера ENDONO является

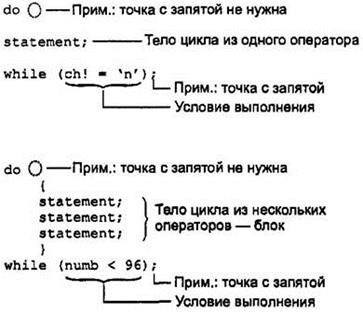
Рис. 3.4. Исполнение цикла while

Цикл do

В цикле while условие продолжения выполнения цикла помещалось в начало цикла. Это означало, что в случае невыполнения условия при первой проверке тело цикла вообще не исполнялось. В некоторых случаях это целесообразно, но возможны и ситуации, когда необходимо выполнить тело цикла хотя бы один раз вне зависимости от истинности проверяемого условия. Для этого следует использовать цикл do, в котором условие продолжения цикла располагается не перед, а после тела цикла.

Наш следующий пример DIVDO выводит приглашение ввести два числа: делимое и делитель, а затем производит целочисленное деление с использованием операций / и % и выводит полученные частное и остаток.

Большая часть программы находится в составе тела цикла do. Ключевое слово do обозначает начало цикла. Затем, как и в других циклах, следует тело, обрамленное фигурными скобками. Завершает цикл условие продолжения, описываемое с помощью ключевого слова while. Это условие похоже на условие цикла while, но у него есть два отличия: оно располагается в конце цикла и завершается точкой с запятой (;). Синтаксис цикла do показал на рис. 3.5.

Рис. 3.5. Синтаксис цикла do

Перед тем как производить вычисление, программа DIVDO спрашивает пользователя, хочет ли он произвести это вычисление, Если в ответ программа получает символ ' y ', то выражение

сохраняет значение true. В случае, если пользователь вводит ' n ', условие продолжения цикла не выполняется и происходит выход из цикла. На рис. 3.6 приведена схема функционирования цикла do.

Вот пример возможного вывода программы DIVDO:

Рис. 3.6. Исполнение цикла do

Выбор типа цикла

Мы рассмотрели основные аспекты использования циклов. Цикл for подходит для тех случаев, когда мы заранее знаем, сколько раз нам потребуется его выполнение. Циклы while и for используются в тех случаях, когда число итераций цикла заранее не известно, причем цикл while подходит в тех случаях, когда тело цикла может быть не исполненным ни разу, а цикл do - когда обязательно хотя бы однократное исполнение тела цикла.

Эти критерии достаточно спорны, поскольку выбор типа цикла больше определяется стилем, нежели строго определенными правилами, Каждый из циклов можно применить практически в любой ситуации. При выборе типа цикла стоит руководствоваться удобочитаемостью и легкостью восприятия вашей программы.

 

· ТЕМА 13. ВЕТВЛЕНИЯ

Управление циклом всегда сводится к одному вопросу: продолжать выполнение цикла или нет? Разумеется, люди в реальной жизни встречаются с гораздо более разнообразными вопросами. Нам нужно решать не только, пойти ли на работу сегодня или нет (продолжить ли цикл), но и делать более сложный выбор, например, купить ли нам красную футболку или зеленую (или вообще не покупать футболку) или взять ли нам отпуск и, в случае положительного отпета, провести его в горах или на море?

Программам тоже необходимо принимать решения. В программе решение, или ветвление, сводится к переходу в другую часть программы а зависимости от значения соответствующего выражения.

В C++ существует несколько типов ветвлений, наиболее важным из которых является if... else,осуществляющее выбор между двумя альтернативами. В операторе ветвления if... else использование else не является обязательным. Для выбора одной из множества альтернатив используется оператор ветвления switch, действие которого определяется набором значений соответствующей переменной. Кроме того, существует так называемая условная операция, используемая в некоторых особых ситуациях. Мы рассмотрим каждую из этих конструкций.

 

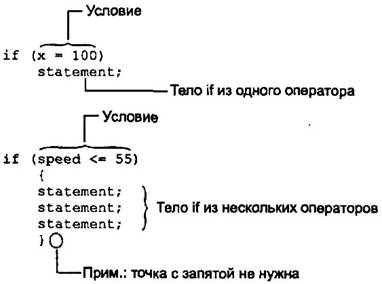
· ТЕМА 14. УСЛОВНЫЙ ОПЕРАТОР IF

Оператор if является наиболее простым из операторов ветвлений. Следующая программа, IFDEMO, иллюстрирует применение оператора if.

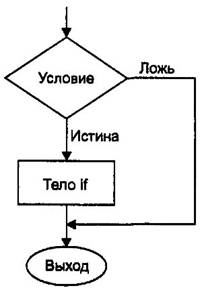
За ключевым словом if следует условие ветвления, заключенное в круглые скобки. Синтаксис оператора if показан на рис. 3.7. Легко заметить, что синтаксис if очень напоминает синтаксис while. Разница заключается лишь в том, что если проверяемое условие окажется истинным, то операторы, следующие за if, будут выполнены всего один раз; операторы, следующие за while, исполняются до тех пор, пока проверяемое условие не станет ложным. Функционирование оператора if показано на рис. 3.8.

Примером работы программы IFDEMO может служить следующий:

Если вводимое число окажется не превосходящим 100, то программа завершится, не напечатав вторую строку.

Рис. 3.7. Синтаксис оператора if

Рис. 3.8. Исполнение оператора If

 

· МОДУЛЬ 2. ПОИСК

 

· ТЕМА 1. ЛИНЕЙНЫЙ ПОИСК

Если нет никакой дополнительной информации о разыскиваемых данных, то очевидный подход - простой последовательный просмотр массива с увеличением шаг за шагом той его части, где желаемого элемента не обнаружено. Такой метод называется линейным поиском. Условия окончания поиска таковы:

1. Элемент найден, т.е. а _i = х.

BEGIN

m: = (L + R) DIV 2; { выбираем любой элемент между элементами с номерами L и R }

IF a[m]=x THEN found: = TRUE ELSE

IF a[m] < x THEN L: = m + 1 ELSE R: =m – 1;

END;

IF found THEN writeln(‘ искомый элемент ‘, a [m]);

Инвариант цикла, т.е. условие, выполняющееся перед каждым шагом, таков:

(L ≤ R) & (A k: 1 ≤ k < L: a_k < х) & (A k: R < k ≤ N: a_k > х) (5.6)

из чего выводится результат

found OR ((L > R) & (A k: 1 ≤ k < L: a_k < х) & (A k: R < k ≤ N: a_k > х))

откуда следует

(a_m = x) OR (A k: 1 ≤ k ≤ N: a_k ≠ х).

Выбор m совершенно произволен в том смысле, что корректность алгоритма от него не зависит. Однако на его эффективность выбор влияет. Ясно, что наша задача - исключить на каждом шагу из дальнейшего поиска, каким бы ни был результат сравнения, как можно больше элементов. Оптимальным решением будет выбор среднего элемента, так как при этом в любом случае будет исключаться половина массива. В результате максимальное число сравнений равно log₂ (N), округленному до ближайшего целого. Таким образом, приведенный алгоритм существенно выигрывает по сравнению с линейным поиском, ведь там ожидаемое число сравнений - N / 2.

Эффективность можно несколько улучшить, поменяв местами заголовки условных операторов. Проверку на равенство можно выполнять во вторую очередь, так как она встречается лишь единожды и приводит к окончанию работы. Но более существенно следующее соображение: нельзя ли, как и при линейном поиске, отыскать такое решение, которое опять бы упростило условие окончания. И мы действительно находим такой быстрый алгоритм, как только отказываемся от наивного желания кончить поиск при фиксации совпадения. На первый взгляд это кажется странным, однако при внимательном рассмотрении обнаруживается, что выигрыш в эффективности на каждом шаге превосходит потери от сравнения с несколькими дополнительными элементами. Напомним, что число шагов в худшем случае - log₂ (N). Быстрый алгоритм основан на следующем инварианте:

(A k: 1 ≤ k < L: a_k < х) & (A k: R < k ≤ N: a_k ≥ х) (5.7)

причем поиск продолжается до тех пор, пока обе секции не «накроют» массив целиком.

L:= 1; R: = N + 1;

WHILE L<R DO

BEGIN

j: = (L + R) DIV 2;

IF a [j] < x THEN L:= j + 1 ELSE R: = j;

END;

IF a [R] = x THEN writeln(‘ искомый элемент ‘, a [R]);

Условие окончания - L ≥ R, но достижимо ли оно? Для доказательства этого нам необходимо показать, что при и всех обстоятельствах разность R – L на каждом шаге убывает. В начале каждого шага L < R. Для среднего арифметического m справедливо условие L ≤ m < R. Следовательно, разность действительно убывает, ведь либо L увеличивается при присваивании ему значения m + 1, либо R уменьшается при присваивании значения m. При L = R повторение цикла заканчивается. Однако наш инвариант и условие L = R еще не свидетельствуют о совпадении. Конечно, при R = N + 1 никаких совпадений нет. В других же случаях мы должны учитывать, что элемент а [R] в сравнениях никогда не участвует. Следовательно, необходима дополнительная проверка на равенство а [R] = х. В отличие от первого нашего решения (5.5) приведенный алгоритм, как и в случае линейного поиска, находит совпадающий элемент с наименьшим индексом.

 

 

· МОДУЛЬ 3. СОРТИРОВКА

 

· ТЕМА 1. ВНУТРЕННЯЯ И ВНЕШНЯЯ СОРТИРОВКИ

В этой части мы будем обсуждать методы сортировки информации. В общей постановке задача ставится следующим образом. Имеется последовательность однотипных записей, одно из полей которых выбрано в качестве ключевого (далее мы будем называть его ключом сортировки). Тип данных ключа должен включать операции сравнения («=», «>», «<», «>=» и «<=»). Задачей сортировки является преобразование исходной последовательности в последовательность, содержащую те же записи, но в порядке возрастания (или убывания) значений ключа. Метод сортировки называется устойчивым, если при его применении не изменяется относительное положение записей с равными значениями ключа. Устойчивость сортировки часто бывает желательной, если речь идет об элементах, уже упорядоченных (отсортированных) по некоторым вторичным ключам (т.е. свойствам), не влияющим на основной ключ.

Различают сортировку массивов записей, целиком расположенных в основной памяти (внутреннюю сортировку), и сортировку файлов, хранящихся во внешней памяти и не помещающихся полностью в основной памяти (внешнюю сортировку). Для внутренней и внешней сортировки требуются существенно разные методы. В этой части мы рассмотрим наиболее известные методы внутренней сортировки, начиная с простых и понятных, но не слишком быстрых, и заканчивая не столь просто понимаемыми усложненными методами. Начинать разбор с прямых методов, не трогая быстрых алгоритмов, нас заставляют такие причины:

1. Прямые методы особенно удобны для объяснения характерных черт основных принципов большинства сортировок.

2. Программы этих методов легко понимать, и они коротки. Напомним, что сами программы также занимают память.

3. Усложненные методы требуют небольшого числа операций, но эти операции обычно сами более сложны, и поэтому для массивов достаточно малых размерностей прямые методы оказываются быстрее, хотя для больших массивов их использовать, конечно, не следует.

 

· ТЕМА 2. МЕТОДЫ ВНУТРЕННЕЙ СОРТИРОВКИ

Естественным условием, предъявляемым к любому методу внутренней сортировки является то, что эти методы не должны требовать дополнительной памяти: все перестановки с целью упорядочения элементов массива должны производиться в пределах того же массива. Мерой эффективности алгоритма внутренней сортировки являются число требуемых сравнений значений ключа (C) и число перестановок элементов (M).

Заметим, что поскольку сортировка основана только на значениях ключа и никак не затрагивает оставшиеся поля записей, можно говорить о сортировке массивов ключей.

Методы сортировки «на том же месте» можно разбить в соответствии с определяющими их принципами на три основные категории:

1. Сортировки с помощью включения (by insertion).

2. Сортировки с помощью выбора (by selection).

3. Сортировки с помощью обменов (by exchange).

Сортировка включением

Одним из наиболее простых и естественных методов внутренней сортировки является сортировка с простыми включениями. Идея алгоритма очень проста. Пусть имеется массив ключей a[1], a[2],..., a[n]. Для каждого элемента массива, начиная со второго, производится сравнение с элементами с меньшим индексом (элемент a[i] последовательно сравнивается с элементами a[i – 1], a[i – 2]...) и до тех пор, пока для очередного элемента слева a[j] выполняется соотношение a[j] > a[i], a[i] и a[j] меняются местами. Если удается встретить такой элемент a[j], что a[j] <= a[i], или если достигнута нижняя граница массива, производится переход к обработке элемента a[i + 1] (пока не будет достигнута верхняя граница массива).

Легко видеть, что в лучшем случае (когда массив уже упорядочен) для выполнения алгоритма с массивом из n элементов потребуется n – 1 сравнение и 0 пересылок. В худшем случае (когда массив упорядочен в обратном порядке) потребуется n(n – 1)/2 сравнений и столько же пересылок. Таким образом, можно оценивать сложность метода простых включений как O(n ² ).

Можно сократить число сравнений, применяемых в методе простых включений, если воспользоваться тем фактом, что при обработке элемента a[i] массива элементы a[1], a[2],..., a[i – 1] уже упорядочены, и воспользоваться для поиска элемента, с которым должна быть произведена перестановка, методом двоичного деления. В этом случае оценка числа требуемых сравнений становится O(n log n). Заметим, что поскольку при выполнении перестановки требуется сдвижка на один элемент нескольких элементов, то оценка числа пересылок остается O(n² ).

Таблица 5.1

Пример сортировки методом простого включения

В реальном процессе поиска подходящего места удобно, чередуя сравнения и движения по последовательности, как бы просеивать a [ i ], т.е. a [ i ] сравнивается с очередным элементом a [ j ], а затем либо a [ i ] вставляется на свободное место, либо a [ j ] сдвигается (передается) вправо и процесс «уходит» влево. Обратите внимание, что процесс просеивания может закончиться при выполнении одного из двух следующих различных условий:

1. Найден элемент a [ j ] с ключом, меньшим чем ключ у a [ i ].

2. Достигнут левый конец готовой последовательности.

FOR i: = 2 TO N DO BEGIN

x: = a[i]; j: = i;

WHILE (a[j – 1] > x) AND (j > 1) DO BEGIN

a[j]: = a[j – 1];

j: =j – 1

END;

a[j]: = x;

END;

Обменная сортировка

Простая обменная сортировка (в просторечии называемая «методом пузырька») для массива a[1], a[2],..., a[n] работает следующим образом. Начиная с начала массива сравниваются два соседних элемента (a[ i ] и a[ i + 1]). Если выполняется условие a[ i ] > a[ i + 1], то значения элементов меняются местами. Процесс продолжается для a[ i + 1] и a[ i + 2] и т.д., пока не будет произведено сравнение a[ n – 1] и a[ n ]. Понятно, что после этого на месте a[ n ] окажется элемент массива с наибольшем значением. На втором шаге процесс повторяется, но последними сравниваются a[ n – 2] и a[ n – 1]. И так далее. На последнем шаге будут сравниваться только текущие значения a[1] и a[2]. Понятна аналогия с пузырьком, поскольку наименьшие элементы (самые «легкие») постепенно «всплывают» к верхней границе массива.

Для метода простой обменной сортировки требуется число сравнений n(n – 1)/2, минимальное число пересылок 0, а среднее и максимальное число пересылок - O(n ² ).

Метод пузырька допускает три простых усовершенствования. Во-первых, можно отслеживать момент на котором массив окажется отсортированным. Если на некотором шаге не было произведено ни одного обмена, то выполнение алгоритма можно прекращать. Во-вторых, можно запоминать наименьшее значение индекса массива, для которого на текущем шаге выполнялись перестановки. Очевидно, что верхняя часть массива до элемента с этим индексом уже отсортирована, и на следующем шаге можно прекращать сравнения значений соседних элементов при достижении такого значения индекса.

i: = 0;

REPEAT

fl: = TRUE; i: = i + 1;

FOR j: = 1 TO n – i DO

IF a[j] > a[j + 1] THEN BEGIN

fl: = FALSE; x: = a[j];

a[j]: = a[j + 1]; a[j + 1]: = x

END;

UNTIL fl;

Метод пузырька работает неравноправно для «легких» и «тяжелых» значений. Легкое значение попадает на нужное место за один шаг, а тяжелое на каждом шаге опускается по направлению к нужному месту на одну позицию.

На этих наблюдениях основан метод шейкерной сортировки (ShakerSort). При его применении на каждом следующем шаге меняется направление последовательного просмотра. В результате на одном шаге «всплывает» очередной наиболее легкий элемент, а на другом «тонет» очередной самый тяжелый.

{шейкер-сортировка по убыванию}

L: = 2; R: = n; k: = n;

REPEAT

FOR j: = R DOWNTO L DO

IF a[j – 1] < a[j] THEN BEGIN

x: = a[j]; a[j]: = a[j – 1]; a[j – 1]: = x; k: = j

END;

L: = k + 1;

FOR j: = L TO R DO

IF a[j – 1] < a[j] THEN BEGIN

x: = a[j]; a[j]: = a[j – 1]; a[j – 1]: = x; k: = j

END;

R: = k – 1;

UNTIL L>R;

Шейкерная сортировка позволяет сократить число сравнений (по оценке Кнута средним числом сравнений является (n ² – n(const + ln n)), хотя порядком оценки по-прежнему остается n ² . Число же пересылок, вообще говоря, не меняется. Шейкерную сортировку рекомендуется использовать в тех случаях, когда известно, что массив «почти упорядочен».

Сортировка выбором

При сортировке массива a[1], a[2],..., a[n] методом простого выбора среди всех элементов находится элемент с наименьшим значением a[i], и a[1] и a[i] обмениваются значениями. Затем этот процесс повторяется для получаемых подмассивов a[2], a[3],..., a[n],... a[j], a[j + 1],..., a[n] до тех пор, пока мы не дойдем до подмассива a[n], содержащего к этому моменту наибольшее значение. Работа алгоритма иллюстрируется примером в таблице 5.2.

Таблица 5.2

Пример сортировки простым выбором

Для метода сортировки простым выбором требуемое число сравнений - n(n – 1)/2. Порядок требуемого числа пересылок (включая те, которые требуются для выбора минимального элемента) в худшем случае составляет O(n2). Однако порядок среднего числа пересылок есть O(n*ln(n)), что в ряде случаев делает этот метод предпочтительным.

FOR i: = 1 TO n – 1 DO BEGIN

x: = a[i]; k: = i;

FOR j: = i + 1 TO n DO

IF a[j]<x THEN BEGIN x: = a[j]; k: = j END;

a[k]: = a[i]; a[i]: = x;

END;

Сравнение прямых методов внутренней сортировки

Для рассмотренных в начале этой части простых методов сортировки существуют точные формулы, вычисление которых дает минимальное, максимальное и среднее число сравнений ключей (C) и пересылок элементов массива (M). Таблица 5.3 содержит данные, приводимые в книге Никласа Вирта.

Таблица 5.3

Пример сортировки методом Шелл

В общем случае алгоритм Шелла естественно переформулируется для заданной последовательности из t расстояний между элементами h1, h2,..., ht, для которых выполняются условия h t = 1 и h _{(i + 1)} < h _i . Дональд Кнут показал, что при правильно подобранных t и h сложность алгоритма Шелла является O(n ^(1.2) ), что существенно меньше сложности простых алгоритмов сортировки.

На первый взгляд можно засомневаться; если необходимо несколько процессов сортировки, причем в каждый включаются все элементы, то не добавят ли они больше работы, чем сэкономят? Однако на каждом этапе либо сортируется относительно мало элементов, либо элементы уже довольно хорошо упорядочены и требуется сравнительно немного перестановок,

Ясно, что такой метод в результате дает упорядоченный массив, и, конечно же, сразу видно, что каждый проход от предыдущих только выигрывает (так как каждая i-сортировка объединяет две группы, уже отсортированные 2 i -сортировкой). Так же очевидно, что расстояния в группах можно уменьшать по-разному, лишь бы последнее было единичным, ведь в самом плохом случае последний проход и сделает всю работу. Однако совсем не очевидно, что такой прием «уменьшающихся расстояний» может дать лучшие результаты, если расстояния не будут степенями двойки. Поэтому приводимая программа не ориентирована на некую определенную последовательность расстояний. Каждая h-сортировка программируется как сортировка с помощью прямого включения.

k: = n;

WHILE k > 1 DO BEGIN

k: = k DIV 2;

FOR i: = k + 1 TO n DO BEGIN

x: = a[i]; j: = i;

WHILE (x < a[j – k]) AND (j>i – k) DO BEGIN

a[j]: = a[j – k];

j: = j – k;

END;

a [ j ]: = x;

END;

END;

Анализ сортировки Шелла. Анализ этого алгоритма поставил несколько весьма трудных математических проблем, многие из которых так еще и не решены. В частности, не известно, какие расстояния дают наилучшие результаты. Но вот удивительный факт: они не должны быть множителями один другого. Это позволяет избежать явления уже очевидного из приведенного выше примера, когда при каждом проходе взаимодействуют две цепочки, которые до этого нигде еще не пересекались. И действительно, желательно, чтобы взаимодействие различных цепочек проходило как можно чаще. Справедлива такая теорема: если k-отсортированную последовательность i-отсортировать, то она остается k-отсортированной. Кнут показывает, что имеет смысл использовать такую пос