
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дуги Пропускные способности дугСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
I. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ТЕОРИИ ГРАФОВ Будем придерживаться терминологии из [1]. Ориентированным графом (орграфом) G=(Х, Г) называется пара (X, Г), где X - множество элементов, называемых вершинами, а Г -многозначное отображение Х =>Х. Многозначное отображение Х=>Х есть закон, по которому каждому элементу x принадлежащему Х ставится.в соответствие некоторое подмножество Гx множества Х. Дугами орграфа называется упорядоченные пары (x, y) принадлежащие Х*Х, y Î Гх. Если обозначить через U множество всех дуг графа, то граф можно определить, как G= (X,U) Вершина x называется началом дуги u = (x, y), а вершина y - ее концом. Дуга (x, x), начало и конец которой совпадают, называется петлей. Две различные вершины x и y называются смежными, если существует соединяющая их дуга. Полустепенью захода вершины называется число дуг, заходящих я вершину, а полустепенью исхода - исходящих из вершины. Вершина S с нулевой полустепенью захода называется входом орграфа, а вершина t с нулевой полустепенью исхода - выходом орграфа. Путем L (a, б) из вершины а, в вершину b называется последовательность вершин и дуг a, (a, x1), x1, (x1, x2)…,(xn-1, b),b. Заметим, что в орграфе путь однозначно определяется последовательностью вершин или дуг. Путь называется простым, если вершины не, повторяются. Если существует путь L(a, 6), то говорят, что вершина b достижима из вершины a. Орграф называется связным, если для любой пары вершин одна достижима из другой. Путь L (a, a), начала и конец которого совпадают, называется контуром. Пусть X1, X2 Ì X, X1 ÇX2=0, X1 U X2=X. Тогда множество <X1, X2> таких дуг, что для каждой дуги (х, у) Î <X1, X2> выполняется условие, x ÎX2, y ÎX2 буден называть разрезом графа G = (X, U). Неориентированным графом называется пара (X, U), где X - множество вершин, а U - множество неупорядоченных пар элементов из X, называемых ребрами. Для неориентированного графа имеются почти все аналоги выше определенныx понятий. Две вершины смежны, если они соединены; ребро инцидентно своим концевым вершинам; последовательность таких вершин x1, x2, …,xn, что (xi-1, xi) ÎU образуют цепь; цепь, у которой совпадают концевые вершины, называется циклом; цепь и цикл являются простыми, есливершины не повторяются; две вершины х, y являются связанными, если существует путь L (x, y). Двудольным графом G= (R U S,U) называется граф для каждого ребра (x, y) ÎU которого выполняется условие x ÎR, y Î S, т.е. инцидентные вершины всех ребер принадлежат двум разным подмножествам вершин. Для описания графа будем использовать матрицу смежности или списки смежности. Матрицей смежности называется квадратная матрица Р, у которой pij=1, если (xi,xjÎU (в случае взвешенного графа элемент pij равен весу дуги (ребра)), в противном случав pij=0. Списки смежности перечисляют для каждой вершины x ÎX множества Гх, т.е. концов всех дуг, исходящих из вершины x. КРАТЧАЙШИЕ ПУТИ Пусть G = (X, Г) - ориентированный граф, каждой дуге (x, y) которого приписано положительное число w (x, y), называемое длиной дуги. Длиной пути называют сумму длин входящих в него дуг. Путь, имеющий наименьшую длину среди всех путей из s в t называют кратчайшим путем из s в t, а его длину - расстоянием между s и t. Задача I. Необходимо найти кратчайшие пути и расстояния между данной вершиной s и всеми другими вершинами графа. Рассмотрим алгоритм Дейкстры [2, 7]. Входными данными является орграф G=(X, Г), матрица весов W={w(x, y)}; x, y ÎX (все веса неотрицательные). Опишем алгоритм Дейкстры, используя алголоподобный язык. алгоритм I. 1) начало; 2) для v ÎX выполнить D(x):=w(i, v); D(s):=0; 3) T:=X\{s}; 4) пока T <> 0 выполнить; 5) начало; 6) u:= произвольная вершина r ÎT: D(r) = min {D(p): p ÎT /постоянная метка./; и для всех y ÎT (r) w(y, r)=M 7) T:=T\{u}; 8) для v Î T выполнить D(v):=min(D(v), D(u) + w(u, v)); /временные метки/; 9) конец; 10) конец. В итоге работы алгоритма получим расстояния от вершины s до всех вершин графа (массив D(v)).
Очевидно, что при входе в цикл 4 выполняются следующие условия: 1) для каждой v Î X\T D(v) = d(s, v), где d(s, v) - кратчайшее расстояние от вершины s до вершины v; 2) для каждой v Î T D(v) есть длина кратчайшего из тех путей из s, для которых предпоследняя вершина ÎV\T.(1) В строке 6 алгоритма находим u Î Т, такую, что D(u) есть минимальное значение для всех u ÎТ. В этом случае D(u) = d(s, u), так как если кратчайшее расстояние из s в u меньше D(u), то в силу второй части условия (I) предпоследняя вершина этого пути принадлежит Т. Пусть t - первая вершина пути, принадлежащая множеству Т. Начальный отрезок пути из S в U (путь s-t.) составляет кратчайший путь из s в t, причем его предпоследняя вершина не принадлежит Т. Тогда, учитывая (I), имеем D(t) = d(s, t). Так как все веса неотрицательные, получим: D(t) £ d(s, u) < D(u),что противоречит принципу, по которому была выбрана вершина u. Т.о. D(u) = d(s, u) и в строке 7мы уделяем вершину u из Т. В цикле 8 проверяются пути из s в v Î Т, предпоследняя вершина в которых есть U. Оценим сложность алгоритма Дейкстры. Цикл 4 выполняется (n-1) раз, и каждое его выполнение требует o(n) шагов, (за • (n)) шагов находится вершина U в строке 6 и за o(n) шагов выполняется цикл 8). Таким образом, сложность алгоритма есть о(n2). Пример I. Пусть в графе на рис.1 требуется найти кратчайшие пути из вершины s во все другие вершины графа. Длины дуг обозначены числами возле соответствующей дуги. Последовательное изменение меток вершин показано в табл.1. Окончательное распределение меток и кратчайшие пути показаны на рис.2.
Таблица 1.
Контрольные вопросы и задания 1. Докажите корректность алгоритма Дейкстры. 2. Приведите пример некорректности алгоритма в случае нарушения условия w (i, j) > 0 для всех (i, j) ÎU. 3. Предложите модификацию алгоритма, допускающую отрицательные значения весов дуг. 4. Укажите последовательное изменение меток для длин дуг, приведенных в табл.2, для графа, изображенного на рис.1. 5. Предложите модификацию алгоритма, если требуется найти кратчайший путь и его длину между двумя вершинами графа.
Таблица 2.
Задача 2. Необходимо найти кратчайшие пути между всеми парами вершин графа G. Рассмотрим алгоритм Флойда [1,2]. Пусть вершины графа G обозначены числами 1,2,..., n. Алгоритм строит последовательность матриц W(0), W(1), W(2),..., W(n) следующим образом: W(k) : wij(k) =min{wij(k - 1),wik(k - 1)+wkj(k - 1)},1 £ k £ n, (2) w(i, j), если (i, j) Î U, W(0) : wij(0) = ¥, если (i, j) Ï U, 0, если i = j. Элемент wij(n) матрицы W(n) равен расстоянию между вершинами i и j. Обоснуем уравнение (2). Рассмотрим кратчайший путьиз xi в xj с промежуточными вершинами из множества {x1, …, x k-1, xk}. Если этот путь не содержит xk, то, wij(k) = wij(k-1) деля путь на отрезки от xi до xk и от xk до xj, получаем равенство wij(k) = wik(k -1) + wkj(k -1). Минимум в (2) ищется по той причине, что необходимо определить кратчайшие расстояния между вер-шинами. Для определения кратчайших путей одновременно с последовательностью матриц { w(k) } строится последовательность матриц Z(0), Z(1), …, Z(n) , где Z(k): zij(k) = zij(k -1), если wij(k –1) £ wik(k-1) + wkj(k -1). (4 ) zik(k –1) в противном случае. Z(0): zij(0) = j, если (i, j) ÎU 0 в противном случае. (5)
Элемент zij(n) матрицы Z(n) указывает на первую вершину после i в кратчайшем пути из i в j. Кратчайший путь (i, i1, i2, …, ip, j) из вершины i в вершину j определяется по матрице Z(n) следующим образом: i1 = Zij(n), i2 = Zi1j(n), i3 = Zi2j(n),…,j = z(n)ipj. Входом алгоритма являются матрицы W(0) и Z(0) , построенные в соответствие с (3) и (5). Пусть W(0) = {wij}, Z(0) = {zij}, ¥ -достаточно большое число М. Алгоритм 2. начало 1) для k от 1 до n шаг 1 цикл; 2) начало; 3) для i от 1 до n шаг 1 цикл; 4) начало; 5) для j от 1 до n шаг 1 цикл; 6) начало; 7) если wik + wkj < wij, то; 8) wij:= wik + wkj; 9) zij:= zik; 10) конец цикла; 11) конец цикла; 12) конец цикла; конец Сложность этого алгоритма есть o(n3), так как алгоритм состоит из трех вложенных циклов, каждый из которых выполняется n раз. Пример 2. Пусть в графе, матрица которого представлена в форме табл.3, требуется найти кратчайшие пути между всеми парами вершин. Промежуточные результаты работы алгоритма представлены в табл. 5-14. Окончательные результаты представлены в табл. 15 и 16
Таблица 3 W(0) 1 2 3 4 5 6
Таблица 4 Z(0) 1 2 3 4 5 6
Таблица 5 W(1) 1 2 3 4 5 6
Таблица 6 Z(1) 1 2 3 4 5 6
Таблица 7 W(2) 1 2 3 4 5 6
Таблица 8 Z(2) 1 2 3 4 5 6
Таблица 9 W(3) 1 2 3 4 5 6
Таблица 10 Z(3) 1 2 3 4 5 6
Таблица 11 W(4) 1 2 3 4 5 6
Таблица 12 Z(4) 1 2 3 4 5 6
Таблица 13 W(5) 1 2 3 4 5 6
Таблица 14 Z(5) 1 2 3 4 5 6
Таблица 15 W(6) 1 2 3 4 5 6
Таблица 16 Z(6) 1 2 3 4 5 6
Контрольные вопросы и задания I. Докажите корректность алгоритма Флойда. 2. Покажите, что матрица Р., полученная из матрицы W(n) следующим образом pij = 0, если wij(n) = 0 или M 1 в противном случае, является матрицей достижимости графа G. 3. Покажите, что если wij < 0, то вершина i принадлежит контуру с отрицательной длиной. 4. Предложите процедуру определения кратчайших путей по матрице W(0) и W(n) 5. Покажите, что многократное использование алгоритма Дейкстры для нахождения кратчайших путей между всеми парами вершин и алгоритм Флойда имеют одинаковую вычислительную сложность. 6. Предложите модификацию алгоритма Флойда для случая неориентированного графа G. 7. Предложите процедуру определения числа М.
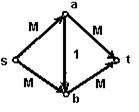
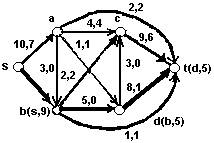
ПОТОКИ В ТРАНСПОРТНОЙ СЕТИ Пусть задан ориентированный грай без петель G (X, U), каждой дуге которого приписано неотрицательное вещественное число c(i, j), называемое пропускной способностью дуги. В графе G имеются две выцеленные вершины s - исток и t - сток. Вершина s имеет только исходящие дуги, а t - входящие. Граф G называется транспортной сетью. Определим на G функцию f, которая каждой дуге ставит в соответствие неотрицательное вещественное число f(i, j) Îc(i, j), причем еi f(i, j) = еi f(i, j) для любого i ¹ s, t. Функция f называется потоком в транспортной сети. Обозначим через Ff величину потока, равную Ff = еi = f (s, i) Необходимо найти поток в транспортной сети G имеющий максимальную величину. Рассмотрим помечивающий алгоритм Форда-Фалкерсона, описывающий последовательное улучшение начального нулевого потока. Пусть в транспортной сети найден некоторый поток f. Если удается найти путь L из s в t. такой, что изменение f(i, j) для (i, j) Î L приводит к увеличению Ff, то строится поток f’,.для которого Ff ‘ < Ff Если такого пути L найти не удается, то поток f является максимальным. Для построения пути L используется процедура помечивания вершин. Вершине, которая помечивается, приписывается пара (x, б). Первый символ в метке (x, б) указывает на вершину, которая непосредственно предшествует данной вершине в пути L. Второй элемент б>0 определяет, на сколько возможно увеличить величину потока f, Путь L считается построенным, если помечена вершина t. Первой получает (-, Ґ) вершина s. Далее вершины помечаются по следующим правилам: 1)пусть вершина x помечена и имеется прямая дуга (x, y) причем f(x, y)<c(x,y). Тогда вершине y может быть приписана метка (x, min { бx, c(x, y) – f(x, y)}); 2) пусть вершина x домечена и имеется обратная дуга (y, x) причем f(y, x) > 0. Тогда вершина y может быть приписана метка (x, min {бx, f(y, x)}. Помечиванием вершины t заканчивается построение f - дополняющего пути L, всем вершинам которого приписаны метки. В транспортной сети определяется новый поток f’ c Ff ’ = Ff+бt. f(i, j)+бt, если (i, j) – прямая дуга L f’(i, j) = f(i, j) - бt, если (i, j) – обратная дуга L f(i, j), если (i, j) ÎU \ L. Работа алгоритма заканчивается, если вершина i не помеченаи невыполняется условие помечиванияни для одной вершины транспортной сети при потоке f. Найденный поток f является максимальным. В рассмотренном только что алгоритме выбор дополняющего пути (если он существует) осуществляется произвольным образом. Проиллюстрируем на примере проблему, к которой может привести произвольность выбора.
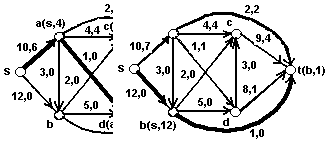
Предположим, что мы начинаем с нулевого потока и поочередно используем пути: P1: s,a,b,t P2: s,b,a,t в качестве дополняющих путей. На каждом ваге величина потока увеличивается точно на I, а максимальный поток величиной 2М достигается через 2М шагов, т.е. сложность алгоритма не зависит от числа вершин и ребер в сети, а определяется функцией от пропускной способности М, которая может быть сколь угодно большой. Целесообразно строить f - дополняющие пути таким образом, чтобы они были кратчайшими (в смысле числа дуг). Для этого достаточно использовать дисциплину «первым пришел? - первым обслужен», т.е. сначала надо пытаться пометить смежные вершины той вершины, которая была раньше помечена. В этом случае сложность алгоритма не зависит от пропускных способностей дуг, а определяется только графом G. Доказано [7], что если в алгоритме Форда-Фалкерсона каждое увеличение потока выполняется вдоль кратчайшего дополняющего пути, то максимальный поток можно получить не более,чем после m(n+2)/2 приращений величины потока, где m. - число дуг, n. -число вершин в транспортной сети. Так как дополняющий путь можно найти за 0(m) шагов, то отсюда следует, что модифицированный алгоритм имеет сложность 0(m2*n). Алгоритм 3. начало 1) провести поиск в ширину и занумеровать вершины в соответствии порядком их обхода при этом поиске; 2) положить f(u)=0 для всех к u ÎU 3) V:= S; 4) l (s);= M; 5) пока V ¹ 0 и не содержит t цикл; 6) V:= вершина с наименьшим номером в V; 7) для всех x Î Г-1v, не имеющих метки, цикл; 8) если f(x, v) > 0, то 9) l(x):= min {l(v), f (x, v)}; 10) p(x):= v; 11) l(x):= 0; 12) V:= V È {x}; 13) конец цикла; 14) для всех x ÎГv не имеющих метки цикл; 15) если f (v, x) < C (u, x), то; 16) l(x):= min {l(v), c(v, x)-f(v, x)}; 17) p(x):= v; 18) l(x):= 1; 19) V:= V È {x}; 20) конец цикла; 21) V:= V \ {u}; 22) конец цикла; 23) если t Î V, то; 24) начало; 25) пока y ¹ S, цикл; 26) y:= t; 27) если l(y) = 1, то; 29) y:= p(y); 30) если l(y) = 0, то, 31) f(y, p(y)):= f(y, p(y)) - l(t); 32) y:= p(y); 33) конец цикла; 34) снять помечивание вершин и перейти к шагу 3; 35) конец; 36) иначе f максимальный поток; конец. Пример 4. Пусть для транспортной сети на рис.4 требуетсянайти максимальный поток. Пропускные способности дуг и значения потока обозначены парами C(u), f(u) возле соответствующей дуги u, f - дополняющие пути и построенная последовательность потоков показаны на рис.4-10.Максимальный поток изображен на рис.10.
Рис. 4 Рис. 5
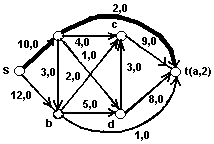
Рис 6. Рис 7.
Рис 8. Рис 9.
Рис 10. Рис 11.
Таблица 17 X Y X Y
x1 ○ x1 ○
x2 ○ x2 ○
○ y5 ○ y5
Рис. 14 Рис. 15
Приведем формулировку теоремы Холла в терминах теории трансверсалей. Пусть P -непустое множество, а S = { S1, S2,…, Sk} – семейство Непустых подмножеств множества P, причем допускается, что Si = SJ при i≠j. Системой различных представителей или трансверсалью семейства S называется множество k различных элементов множества P, по одному из каждого Si. Например, если P= {1,2,3,4,5,6}, S1= {1,3,4}, S2= {1,3,4}, S3= {1,2,5}, S4= {3,6}, то T = {1,3,2,6} множества S1, S2, S3,S4. С другой стороны, если S5= {3,6}, S6= {4}, то для семейства S1, S2, S3,S4,S5,S6 трансверсаль не существует. Задача нахождения трансверсали может быть сведена к задаче построения полного паросочетания в двудольном графе G = (X U Y,E), построенном следующим образом. Поставим во взаимно однозначное соответствие элементы множества вершин двудольного графа X элементам семейства S (xi ↔ Si), а элементам множества Y – элементы множества P (pi ↔ yi). Ребро (xi , yj) Î E тогда и только тогда, когда pi Î Si. Нетрудно заметить, что необходимые и достаточные условия существования трансверсали эквивалентны условиям существования полного паросочетания X с Y. Таким образом, для существования трансверсали семейства подмножеств S множества P необходимо и достаточно чтобы объединение произвольных k подмножеств из S содержало не менее k элементов из P. Пример 6. Построим двудольные графы для двух рассмотренных ранее случаев. На рис.16 приведен граф, когда P= {1,2,3,4,5,6}, S ={S1, S2, S3,S4 }, а на рис.17 – для случая, когда S ={S1, S2, S3,S4,S5,S6}
○ y6 (p6) x 6 ○ ○ y6
Рис. 16 Рис. 17
В первом случае выполняется условие теоремы Холла, а во втором – условие нарушается: |{ x1, x2, x4, x5, x6 }| > |{ y1, y3, y4, y6 }|, а также объединение пяти подмножеств S1, S2, S4, S5, S6 содержит только четыре элемента p1, p3, p4, p6. Следовательно, трансверсаль существует только в первом случае. Рассмотрим алгоритм нахождения максимального паросочетания в двудольном графе G = (X U Y,E) [6]. Построим транспортную сеть, в качестве вершин которой возьмем элементы множеств X и Y, добавив к ним исток s и сток t. Соединим s с каждой вершиной xj ÎX дугой (s, xj) с пропускной способностью, равной 1, а каждую вершину yj ÎY с t дугой (yj,t) с пропускной способностью, также равной 1, а каждую вершину xj ÎX с yj ÎY дугой (xj,yj), если yj Î Гxj, с пропускной способностью, равной ∞. На рис.19 изображена транспортная сеть, соответствующая двудольному графу на рис.18. Нетрудно заметить, что число ребер в максимальном паросочетании равно величине максимального потока в построенной таким образом транспортной сети. Используя алгоритм Эдмондса-Карпа, можно найти максимальное паросочетание за о(m2n) шагов, где m - число дуг, n - число вершин в построенной транспортной сети. Однако особый вид этой сети позволяет построить более эффективный алгоритм, который рассматривается ниже и носит название алгоритма Хопкрофта-Карпа.
x1 ∞ y1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 Пример 3. Рассмотрим транспортную сеть (рис.3), каждой дуге которой приписано число, являющееся пропускной способностью этой дуги (М – сколь угодно большое число). Рис 3.
Пример 3. Рассмотрим транспортную сеть (рис.3), каждой дуге которой приписано число, являющееся пропускной способностью этой дуги (М – сколь угодно большое число). Рис 3.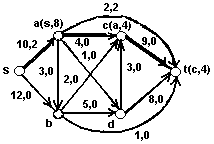




 ○ y1 ○ y1
○ y1 ○ y1

 x3 ○ x3 ○
x3 ○ x3 ○






 ○ y1 (p1) x1 ○ ○ y1
○ y1 (p1) x1 ○ ○ y1
 (S1) x1 ○
(S1) x1 ○


 ○ y2 (p2) x2 ○ ○ y2
○ y2 (p2) x2 ○ ○ y2
 (S2) x2 ○
(S2) x2 ○
 ○ y3 (p3) x3 ○ ○ y3
○ y3 (p3) x3 ○ ○ y3 (S3) x3 ○
(S3) x3 ○
 ○ y4 (p4) x4 ○ ○ y4
○ y4 (p4) x4 ○ ○ y4 (S4) x4 ○
(S4) x4 ○ ○ y5 (p5) x 5 ○ ○ y5
○ y5 (p5) x 5 ○ ○ y5




