Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЗАДАЧИ В13 Уважаемые выпускники, все задачи В13 из банка заданий ФИПИ решаются по единому алгоритму. Задания на движение или на работу однотипны. Главное — знать к ним подход. Всё, что нужно — это здравый смысл и умение решать квадратное уравнение. Кроме этого к В13 относятся задачи на смеси, сплавы, прогрессии, проценты. Вы поймёте, что и в них нет ничего особо сложного.
Сначала предлагаю вам проверить себя – это важно. Запишите в виде математического выражения: 1. 2. 3. 4. 5. Казалось бы, вопросы очень простые. Но почему-то у выпускников они вызывают затруднения. Ученики одиннадцатого класса думают, как записать, что « Итак, правильные ответы: 1. 2. 3. 4. 5.
Задачи на движение. Здесь два правила: 1. Эти задачи решаются по формуле: то есть расстояние 2. В качестве переменной Для начала внимательно читайте условие. В нем всё уже есть. Помните, что текстовые задачи на самом деле труда не представляют. Из «А» в «В» одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в «В» одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 48 км/ч. Ответ дайте в км/ч. Примем скорость первого автомобилиста за Скорость второго на первой половине на 13 км/ч меньше, то есть
Заполним в таблицу:
Известно, что в пункт «В» они прибыли одновременно, то есть затратили одинаковое время:
Примечание: в таблице мы записали путь как S. Можно было записать 1, это можно делать, когда не задана длина пути. Суть не меняется (1путь) или (S км) не важно. В уравнении эта величина сократится:
Получили два решения 52 (км/ч) и 39 (км/ч). Но в условии сказано, что искомая скорость больше 48(км/ч). Ответ: 52
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч. Пусть скорость велосипедиста на пути из «А» в «В» равна х. Тогда его скорость на обратном пути равна х +7. Расстояние в обеих строчках таблицы пишем одинаковое: 98 километров. Осталось записать время.
На обратном пути велосипедист сделал остановку на 7 часов и в результате затратил столько же времени, сколько на пути из «А» в «В». Это значит, что на обратном пути он крутил педали (находился в движении) на 7 часов меньше. Значит,
Или можно рассудить так: велосипедист на обратный путь затратил
D=441 Скорость величина положительная, значит скорость велосипедиста из А в В равна 7 (км/ч). Ответ: 7
Два велосипедиста одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч. Примем скорость второго велосипедиста за х. Тогда скорость первого равна х +3. Расстояние оба проехали одинаковое — 88 километров. Осталось записать время. Поскольку
Сказано, что первый прибыл на три часа раньше, то есть он затратил время на движение и ещё три часа ожидал, пока прибудет второй. Значит время, затраченное первым на передвижение плюс три часа ожидания второго, равно времени нахождения в пути второго.
Можно рассудить по-другому: выражение «первый прибыл на три часа раньше», означает, что он затратил на пробег на три часа меньше, чем второй. То есть
Умножаем левую и правую части на Приводим его к квадратному, получим Решаем его, получим: D=361
Ответ: 8 От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью, на 1 км/ч большей, отправился второй. Расстояние между пристанями равно 420 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч. Примем скорость первого теплохода за Расстояние оба проехали одинаковое — 420 километров. Осталось записать время. Поскольку
Сказано, что через час после отправления первого, в путь отправился второй, то есть он затратил время на движение на час меньше.
Умножаем левую и правую части на Приводим к квадратному, получим Решаем его: Скорость теплохода должна быть положительна, значит, она равна Ответ: 20
Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч. Пусть скорость лодки в неподвижной воде равна Тогда скорость движения моторки по течению равна Расстояние и в ту, и в другую сторону одинаково и равно 255 км. Занесем скорость и расстояние в таблицу. Заполняем графу «время». Мы уже знаем, как это делать. При движении по течению
Условие
Вообще-то это уравнение имеет два корня: Ответ: 16
Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч. Пусть скорость теплохода в неподвижной воде равна x(км/ч). Всего теплоход затрачивает 48 часов (на весь путь: туда, два часа стоянки, обратно). То есть 48 = время движения по течению + стоянка + время движения против течения. Скорость движения теплохода по течению равна Расстояние и в ту, и в другую сторону одинаково и равно 336 км. Занесем скорость и расстояние в таблицу. Заполняем графу «время». Время, затраченное на путь до пункта назначения Время, затраченное на путь обратно (против течения)
Как извлечь корень из 148996, или из другого большого числа? Советую воспользоваться аналитическим методом. Каким бы большим ни было число (кстати, в подобных задачах на ЕГЭ больше 1000000 не будет), мы в любом случае можем определить, между какими значениями лежит результат корня. В нашем случае он находится между 300 и 400,
Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел. Разность
Значит, наш результат больше 370. Далее ясно, так как 148996 оканчивается на 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6, только эти числа при возведении в квадрат дают в конце 6. Поэтому проверяем числа 374,376, 384, 386, 394…
Мы установили, что корень из 148996 равен 386. Конечно, есть и другие способы извлечения таких корней без калькулятора, но всё-таки произвести пять действий умножения столбиком это не так уж много (а больше и не понадобится, если вы грамотно оцените в каких пределах лежит искомое значение). Скорость теплохода в неподвижной воде 19(км/ч). Ответ: 19 Теплоход проходит по течению реки до пункта назначения 216 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 6 часов, а в пункт отправления теплоход возвращается через 36 часов после отплытия из него. Ответ дайте в км/ч. От предыдущей эта задача отличается только тем, что нужно найти скорость течения, при известной скорости теплохода. Ход рассуждения тот же. Скорость течения реки как искомую величину принимаем за x(км/ч). Тогда скорость движения теплохода по течению равна Расстояние в ту, и в другую сторону одинаковое и равно 216 км. Всего теплоход затрачивает 36 часов (на весь путь: туда, 6 часов стоянки, обратно). То есть 36 = время движения по течению + стоянка + время движения против течения. Занесем скорость и расстояние в таблицу. Заполняем графу «время». Время, затраченное на путь до пункта назначения Время, затраченное на путь обратно (против течения)
Подставляем данные и получаем уравнение:
Мы не будем подробно останавливаться на технике решения уравнения. Всё уже понятно — раскрываем скобки, складываем подобные члены. Получаем квадратное уравнение: Поскольку скорость течения положительна, получаем: Ответ: 3
Байдарка в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка отправилась назад и вернулась в пункт А в 16:00. Определите (в км/час) собственную скорость байдарки, если известно, что скорость течения реки 2 км/ч. Данная задача от предыдущих двух отличается только тем, что в ней несказанно, сколько байдарка затратила время на путь (дан временной отрезок пути), и время стоянки задано не в целых часах. Сам тип задачи тот же. Сразу определим время нахождения байдарки в пути 16-10=6(часов). Так же выразим время стоянки в часах 1ч 20мин это Можно осуществлять перевод в часы с помощью пропорции: 60мин – 1час 80 мин – х
Пусть скорость байдарки в неподвижной воде равна x(км/ч). Тогда скорость движения по течению равна Расстояние и в ту, и в другую сторону одинаково и равно 15 км. Всего время нахождения в пути 6 часов (на весь путь: туда, То есть 6 = время движения по течению + стоянка + время движения против течения. Занесем скорость и расстояние в таблицу. Заполняем графу «время». Время, затраченное на путь до пункта назначения Время, затраченное на путь обратно (против течения)
Составляем уравнение:
Не забываем, что скорость величина положительная. Таким образом, собственная скорость байдарки в неподвижной воде будет 7(км/ч). Ответ: 7
Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч. Вы, наверное, заметили, что это задача схожа с предыдущей. Сразу отметим, что автомобили встретись в 180 км от города «В». Это значит, что тот, кто выехал из «В» проехал 180 км, а кто выехал из «А» проехал 330-180=150 км. Время движения 3 часа. Значит, что скорость выехавшего из «А» равна Составлять таблицу в данной задаче не обязательно. Ответ: 50
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам? В этой задаче ни время движения, ни скорости пешеходов, ни расстояние, которое они прошли. Рекомендую сразу обратить внимание на то, дана разница пройденных расстояний, поэтому сравнение необходимо произвести по расстоянию. Итак, искомую величину (время, через которое расстояние станет равным 300м) примем за Занесем скорость и время в таблицу. Заполняем графу «расстояние».
Так как скорость второго больше, значит именно он пройдёт на 300 метров больше. Незабываем перевести метры в километры 300м=0,3км
Получили Заметьте, что скорость, с которой двигались пешеходы, не играет роли. При разнице в 1,5 км/ч с какой бы скоростью они не двигались, расстояние между ними через 12 минут станет 300м. Вообще для упрощения условия в подобных задачах – при параллельном движении пешеходов, поездов, теплоходов и пр. (в дальнейшем вы это увидите на других примерах) можно принимать скорость одного из объектов движения за ноль. Смотрите, как преобразится задача. Итак, искомую величину (время, через которое расстояние станет равным 300м) примем за Занесем скорость и время в таблицу. Заполняем графу «расстояние».
Так как расстояние между ними через время х будет 0,3 км, то уравнение приобретает вид: Ответ: 12
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого? На первый взгляд тип задачи в сравнении с предыдущей кажется совершенно иным. Имеется круговое движение, длина трасы. Но это только на первый взгляд. Задача точно такая же. Имеем двух мотоциклистов. Один от другого отстаёт на 7 км. Скорость отстающего на 21(км/ч) больше (он догоняет того, кто впереди). Вот вам и задача с прямолинейным движением. Разница расстояния в 7 км между мотоциклистами (половина круга), поэтому сравнение будем проводить по расстоянию. Итак, искомую величину (время, через которое они поравняются) примем за Занесем скорость и время в таблицу. Заполняем графу «расстояние»:
Второй проезжает на 7 км больше, чем находящийся перед ним.
Как видим скорость мотоциклистов в данном случае тоже не имеет значение, как и в предыдущей задаче. Ответ: 20
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч. Пусть скорость третьего велосипедиста x (км/ч), t – время, которое ему понадобилось, чтобы догнать второго. До встречи на трассе они проехали одинаковое расстояние. Известно, что второй ехал на 1 час больше. Составим таблицу:
Таким образом, можем составить уравнение: Продолжаем рассуждение. До встречи на трассе третий и первый проехали одинаковое расстояние. Третий догнал первого через 2 часа 20 минут
Таким образом, можем составить уравнение:
Имеем два уравнения, решаем систему:
Выразим t в первом уравнении и подставим во второе:
t=2/3, так как время не может быть числом отрицательным. Таким образом, Скорость третьего велосипедиста 25 (км/ч). Ответ: 25
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. Данную задачу так же можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т.к. сказано, что на один круг). Найти скорость второго. Очень важно в задачах на движение представить сам процесс этого движения. Сравнение так же производим по расстоянию. За x принимаем искомую величину – скорость второго. Время движения 40 минут (2/3часа) для обоих. Заполним графу «расстояние»:
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
Скорость второго автомобиля 59(км/ч). Ответ: 59
Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. Во-первых, переведем минуты в часы, поскольку скорость надо найти в км/ч. Скорости участников обозначим за Запишем эти данные в таблицу:
Оба проехали одинаковые расстояния, то есть Затем мотоциклист второй раз обогнал велосипедиста. Произошло это через 30 минут, то есть через ½ часа после первого обгона. Нарисуем вторую таблицу:
А какие же расстояния они проехали? Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна 30 км. Получим второе уравнение:
Решим получившуюся систему: Получим, Ответ: 80. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч. Мы не знаем, каким было расстояние, которое преодолел путешественник. Знаем только, что это расстояние было одинаковым на пути туда и обратно. Когда расстояние не указано его принимают за 1 (одно море). Тогда время, которое путешественник плыл на яхте, равно Общее время равно Средняя скорость равна Ответ: 38,4.
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго? На первый взгляд условие очень запутано, может возникнуть мысль, не пропустить ли эту задачу. Рекомендую сделать эскиз (обязательно), обозначить известные величины, наглядность помогает очень часто.
Тёмным цветом обозначена исходная позиция, синим – конечная. Пусть скорость первого сухогр
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1018; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.230 (0.014 с.) |

 на 3 меньше
на 3 меньше 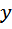
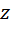 на 8 больше, чем
на 8 больше, чем 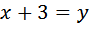


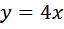
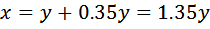
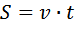 ,
,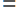 скорость
скорость 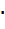 время. Из этой формулы можно выразить скорость
время. Из этой формулы можно выразить скорость 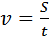 или время
или время  .
. (ч).
(ч). (км/ч). На второй половине пути 78 км/ч, значит время, затраченное им на дорогу
(км/ч). На второй половине пути 78 км/ч, значит время, затраченное им на дорогу



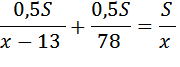

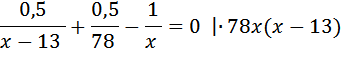
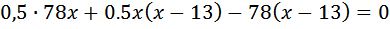

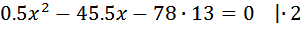
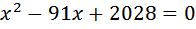

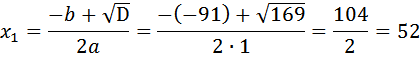
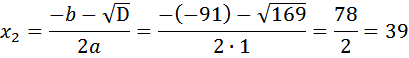
 на путь из «А» в «В» велосипедист затратит время
на путь из «А» в «В» велосипедист затратит время  , а на обратный путь время
, а на обратный путь время 


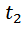 на семь меньше, чем
на семь меньше, чем 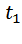 . Получается уравнение:
. Получается уравнение: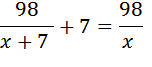
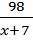 часов и ещё 7 часов простоял. Очевидно, что уравнение будет иметь вышеуказанный вид.
часов и ещё 7 часов простоял. Очевидно, что уравнение будет иметь вышеуказанный вид.
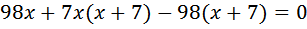

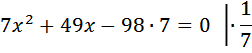


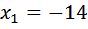
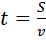 , первый затратит
, первый затратит  =
= 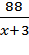 часов, а второй
часов, а второй  часов.
часов.

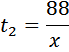

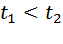 на 3, или
на 3, или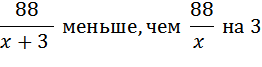
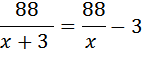
 .
.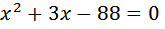
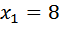

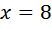 это вполне правдоподобная скорость велосипедиста. А ответ
это вполне правдоподобная скорость велосипедиста. А ответ  не подходит, так как скорость велосипедиста должна быть положительна.
не подходит, так как скорость велосипедиста должна быть положительна.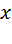 . Тогда скорость второго теплохода равна
. Тогда скорость второго теплохода равна  .
.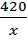 часов, а второй
часов, а второй 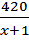 часов.
часов.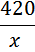

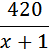
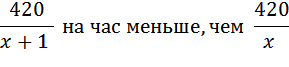
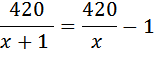
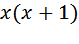 .
.
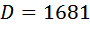
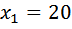
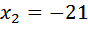
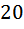 (км/ч).
(км/ч). , а скорость, с которой она движется против течения
, а скорость, с которой она движется против течения  .
.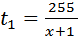 , при движении против течения
, при движении против течения 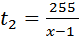 , причем
, причем  на два часа меньше, чем
на два часа меньше, чем  . Да это и логично, что время на движение по течению затрачивается меньше.
. Да это и логично, что время на движение по течению затрачивается меньше.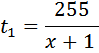

 .
.
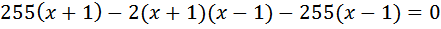
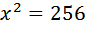
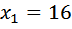 и
и 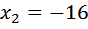 (оба этих числа при возведении в квадрат дают 256). Но, конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
(оба этих числа при возведении в квадрат дают 256). Но, конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.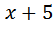 , а скорость против течения
, а скорость против течения 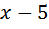 .
. ,
,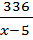 .
.

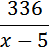


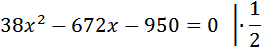

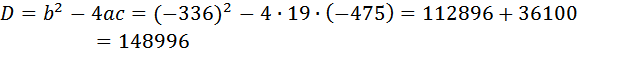
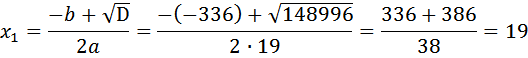

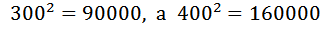 . действительно
. действительно
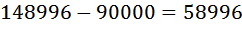 , разность
, разность  . Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360. Далее пробуем возводить в квадрат, например 370, что называется «щупаем» результат.
. Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360. Далее пробуем возводить в квадрат, например 370, что называется «щупаем» результат.

 , а его скорость против течения
, а его скорость против течения  .
. ,
,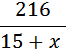
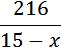


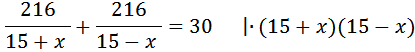
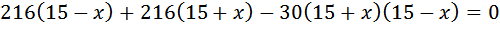

 (км/ч).
(км/ч).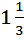 часа.
часа.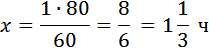
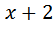 , а скорость против течения
, а скорость против течения 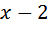 .
.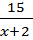 ,
, .
.
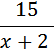


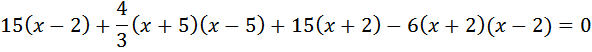

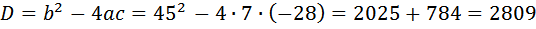

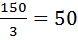 (км/ч).
(км/ч).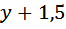 .
.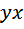
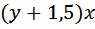
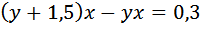
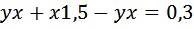
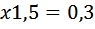
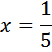
 часа, это 12 минут.
часа, это 12 минут. (он остаётся на месте), тогда скорость второго
(он остаётся на месте), тогда скорость второго 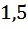 км/ч, так как по условию она на 1,5 км/ч больше.
км/ч, так как по условию она на 1,5 км/ч больше.
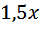
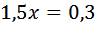
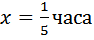
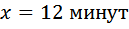
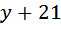 .
.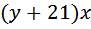
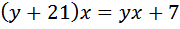
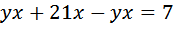
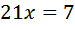
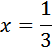
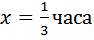 это
это 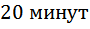
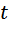
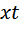
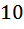

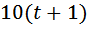
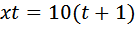
 после того, как догнал второго. Значит, до встречи с первым третий затратил
после того, как догнал второго. Значит, до встречи с первым третий затратил 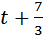 часов, а первый на этот момент уже находился в пути
часов, а первый на этот момент уже находился в пути  (третий выехал через 2 часа после первого, догнал второго -
(третий выехал через 2 часа после первого, догнал второго -  часа догнал первого).
часа догнал первого).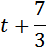
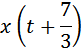
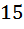
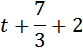
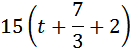
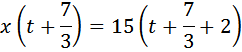
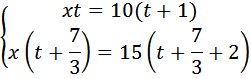
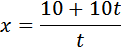
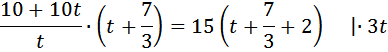
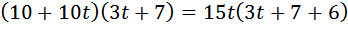
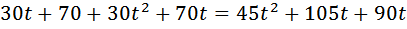
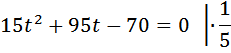

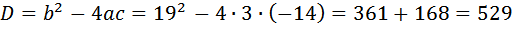
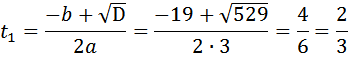
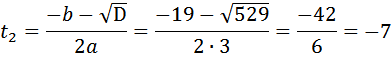
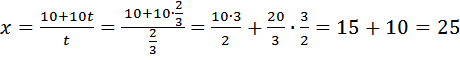 (км/ч)
(км/ч)

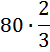

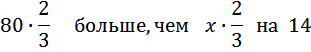
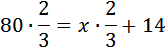


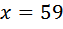
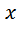 и
и  . В первый раз мотоциклист обогнал велосипедиста через 10 минут, то есть через 1/6 часа после старта. До этого момента велосипедист был в пути 40 минут, то есть 2/3часа.
. В первый раз мотоциклист обогнал велосипедиста через 10 минут, то есть через 1/6 часа после старта. До этого момента велосипедист был в пути 40 минут, то есть 2/3часа.

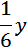
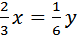 .
.

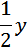
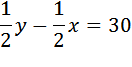
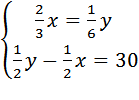
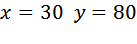 . В ответ запишем скорость мотоциклиста.
. В ответ запишем скорость мотоциклиста.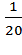 , а время, затраченное на полет, равно
, а время, затраченное на полет, равно 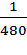 .
.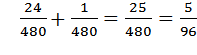
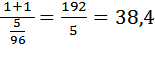 км/ч.
км/ч.