
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фазовые переходы первого и второго рода.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Фазой называется термодинамически равновесное состояние вещества, отличающееся от других возможных равновесных состояний того же вещества. Часто понятие «фаза» употребляется в смысле агрегатного состояния. Переход вещества от одной фазы в другую – фазовый переход – всегда связан с качественными изменениями свойств вещества.Различают фазовые переходы двух родов. Фазовый переход первого рода (например, плавление, кристаллизация и т.д.) сопровождается поглощением или выделением вполне определённого количества теплоты, называемой теплотой фазового перехода. Фазовые переходы первого рода характеризуются постоянством температуры, изменениями энтропии и объёма. Фазовые переходы, не связанные с поглощением или выделением теплоты и изменением объёма, называются фазовыми переходами второго рода. Эти переходы характеризуются постоянством объёма и энтропии, но скачкообразным изменением теплоёмкости. Примерами фазовых переходов второго рода являются: переход ферромагнитных веществ (железа, никеля) при определённых давлении и температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0К, в сверхпроводящее состояние, превращение жидкого гелия при Т=2,9К в сверхтекущию жидкость.Испарение — это процесс, при котором с поверхности жидкости или твердого тела вылетают молекулы, кинетическая энергия которых превышает потенциальную энергию взаимодействия молекул. Испарение сопровождается охлаждением жидкости. Конденсация - экзотермический процесс, при котором вещество переходит в жидкое или твёрдое состояние из газообразного. Плавление – это переход из кристаллического состояния в жидкое.
Основные термодинамические понятия: внутренняя энергия, работа, теплота. Уравнение первого начала термодинамики. Внутренняя энергия – энергия покоя. Внутренняя энергия тела - это сумма кинетической энергии всех молекул, из которых состоит тело, и потенциальной энергии их взаимодействия. Внутренняя энергия зависит от массы и температуры тела, рода вещества и его агрегатного состояния. Внутренняя энергия U одного моля идеального газа равна: U=3/2*RTКоличеством теплоты называется энергия, которую получает или отдает тело при теплопередаче. Если два тела, имеющих разные температуры, привести в тепловой контакт, то возникнет процесс теплопередачи, который всегда направлен от более горячего тела к более холодному. В результате, от горячего тела холодному будет передано некоторое количество теплоты, зависящее от массы тел, рода вещества и первоначальной разности температур. Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и на совершение телом работы: Q=
Зависимость теплоемкости идеального газа от вида процесса. Работа, совершаемая газом при изопроцессах. Процессы, при которых один из параметров p, V или Τ остается постоянным при данной массе аза, называют изопроцессами.Изотермический процесс — это изопроцесс, происходящий при тоянной температуре: Τ = const. Закон изотермического процесса (Бойля-Мариотта): для анной массы газапри постоянной температуре произведение давления на объем есть величина постоянная: p*V=const или для двух состояний p1V2=p2V2.Изобарный процесс — это изопроцесс, происходящий при постоянном давлении: p = const. Закон изобарного процесса: при данной массе газа при постоянном давлении отношение объема к абсолютной температуре есть величина постоянная: V/T=const или V1/T1=V2/T2.Изохорный процесс — это изопроцесс, происходящий при постоянном объеме: V = const. Закон изохорного процесса: при данной массе газа при постоянном объеме отношение давления к абсолютной температуре есть величина постоянная: p/T=const или p1/T1=p2/T2
Адиабатический процесс. Адиабатический процесс (адиабатный процесс) - термодинамический процесс, происходящий в системе без теплообмена с окружающей средой (
22. Цикл Карно и его КПД для идеального газа. Это обратимый круговой процесс, состоящий из двух изотермических и двух адиабатных процессов; впервые рассмотрен французским инженером Л. С. Карно (1824 г.) всвязи с определением КПД тепловых машин. КПД Карно цикла не зависит от свойств рабочего тела (пара, газа и т. п.) и определяется температурами теплоотдатчика Т1 и теплоприемника Т2= (Т1-Т2)/Т1. КПД любой тепловой машины не может быть больше КПД Карно цикла (при тех же Т1 и Т2). Термический КПД цикла Карно, определяется по формуле: 5. Динамические и статистические закономерности в физике. Статистический метод исследования системы. Понятие о функции распределения. две осн. формы закономерной связи явлений, которые отличаются по характеру вытекающих из них предсказаний. В законах динамич. типа предсказания имеют точно определённый, однозначный характер. Так, в механике, если известен закон движения тела и заданы его координаты и скорость, то по ним можно точно определить положение и скорость движения тела в любой др.момент времени. Динамич. законы характеризуют поведение относительно изолированных систем, состоящих из небольшого числа элементов и в которых можно абстрагироваться от целого ряда случайных факторов. В статистич. законах предсказания носят не достоверный, а лишь вероятностный характер. Подобный характер предсказаний обусловлен действием множества случайных факторов, которые имеют место в статистич. коллективах или массовых событиях(напр., большого числа молекул в газе, особей в биологич. популяциях, людей в социальных коллективах). Статистич. закономерность возникает как результат взаимодействия большого числа элементов, составляющих коллектив, и поэтому характеризует не столько поведение отд. элемента, сколько коллектива в целом. Необходимость, проявляющаяся в статистич. законах, возникает вследствие взаимной компенсации и уравновешивания множества случайных факторов. Абсолютизация динамич. законов тесно связана с концепцией механич. детерминизма, сторонники которой (П. Лаплас и др.)рассматривали Вселенную как огромную механич. систему и экстраполировали законы динамики Ньютона на все процессы и явления мира. Лаплас утверждал, что если бы были известны такие законы для всех явлений, то можно было бы обнять в одной формуле движения как величайших тел, так и лег-чайших атомов. Статистич. законы хотя и не дают однозначных и достоверных предсказаний, тем не менее являются единственно возможными при исследовании массовых явлений случайного характера. Критикуя механич. детерминизм, Ф. Энгельс указывал, что случайное не может быть безразличным для науки. Вместе с тем он подчёркивал, что случайное требует иного подхода, ибо изучить всю сеть каузальных отношений, даже с горошинами в стручке, наука совершенно не в состоянии: «... такая наука, которая взялась бы проследить случай с этим отдельным стручком в его каузальном сцеплении со все более отдаленными причинами, была бы уже не наукой, а простой игрой» (Маркс К. и Энгельс Ф., Соч., т. 20, с. 534). За совокупным действием различных факторов случайного характера, которые практически невозможно охватить, статистич. законы вскрывают нечто устойчивое, необходимое, повторяющееся. Статистические законы служат подтверждением диалектики превращения случайного в необходимое. Динамич. законы оказываются предельным случаем статистических, когда вероятность становится практич. достоверностью. С помощью динамич. законов обычно формулируются каузальные (причинные) связи явлений. Рассматривая одно явление как причину другого, мы вырываем их из всеобщей связи, изолируем друг от друга и тем самым значительно упрощаем и идеализируем действительность. Подобную идеализацию легче осуществить в механике, астрономии, классич. физике, которые имеют дело с точно известными силами и законами движения тел под их воздействием. В более сложных ситуациях приходится учитывать воздействие множества случай-ных факторов и обращаться к статистич. законам.
6. Распределение Максвелла. Средние скорости молекул. МА́КСВЕЛЛА РАСПРЕДЕЛЕ́НИЕ, распределение по скоростям частиц (молекул) макроскопической физической системы, находящейся в состоянии термодинамического равновесия, (в отсутствии внешнего поля, при условии, что движение частиц подчиняется законам классической механики. Установлено Дж. К. Максвеллом) в 1859. Закон Максвелла о распределении молекул идеального газа) по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение. При этом на газ не действуют силовые поля. Функция распределения молекул по скоростям f(v)=dN(v)/Ndv определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv и имеет смысл плотности вероятности Для газа, подчиняющегося классической механике, в состоянии статистического равновесия функция распределения f Максвелла по скоростям имеет вид: Средние скорости молекул.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 985; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.008 с.) |

 U+A– это и есть первое начало термодинамики, или закон сохранения энергии в термодинамике. Учитывая правило знаков, первое начало термодинамики можно записать в виде:
U+A– это и есть первое начало термодинамики, или закон сохранения энергии в термодинамике. Учитывая правило знаков, первое начало термодинамики можно записать в виде:  U=Q-A – изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы. Первое начало термодинамики является обобщением закона сохранения энергии для механических и тепловых процессов.
U=Q-A – изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы. Первое начало термодинамики является обобщением закона сохранения энергии для механических и тепловых процессов.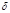 Q=0), т. е. в адиабатически изолированной системе, состояние которой можно изменить только путем изменения внешних параметров. Понятие адиабатической изоляции является идеализацией теплоизолирующих оболочек или сосудов Дьюара (адиабатные оболочки). Изменение температуры внешних тел не оказывает влияния на адиабатически изолированной системы, а их энергия U может изменяться только за счет работы, совершаемой системой (или над ней). Согласно первому началу термодинамики, при обратимом адиабатическом процессе для однородной системы: dQ=dU+pdV=0, где V - объем системы, p - давление. Согласно второму началу термодинамики, при обратимом адиабатическом процессе энтропия постоянна, dS=dQ/T=0, а при необратимом - возрастает. Очень быстрые процессы, при которых не успевает произойти теплообмен с окружающей средой, например, при распространении звука, можно рассматривать как адиабатический процесс. Простым примером адиабатического процесса является сжатие (или расширение) газа в теплоизолированном цилиндре с теплоизолированным поршнем.
Q=0), т. е. в адиабатически изолированной системе, состояние которой можно изменить только путем изменения внешних параметров. Понятие адиабатической изоляции является идеализацией теплоизолирующих оболочек или сосудов Дьюара (адиабатные оболочки). Изменение температуры внешних тел не оказывает влияния на адиабатически изолированной системы, а их энергия U может изменяться только за счет работы, совершаемой системой (или над ней). Согласно первому началу термодинамики, при обратимом адиабатическом процессе для однородной системы: dQ=dU+pdV=0, где V - объем системы, p - давление. Согласно второму началу термодинамики, при обратимом адиабатическом процессе энтропия постоянна, dS=dQ/T=0, а при необратимом - возрастает. Очень быстрые процессы, при которых не успевает произойти теплообмен с окружающей средой, например, при распространении звука, можно рассматривать как адиабатический процесс. Простым примером адиабатического процесса является сжатие (или расширение) газа в теплоизолированном цилиндре с теплоизолированным поршнем. =(Q1-Q2)/ Q1 = A/Q1 (КПД любой тепловой машины). Работа совершаемая газом в изотермических процессах:
=(Q1-Q2)/ Q1 = A/Q1 (КПД любой тепловой машины). Работа совершаемая газом в изотермических процессах:  ;
;  , где А- работа совершенная за 1 цикл. КПД идеальной тепловой машины:
, где А- работа совершенная за 1 цикл. КПД идеальной тепловой машины:  =(T1-T2)/ T1
=(T1-T2)/ T1 
 Подставляя
Подставляя  и интегрируя, мы получим
и интегрируя, мы получим
 — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению
— вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению  . Чтобы найти её, необходимо вычислить
. Чтобы найти её, необходимо вычислить  , приравнять её нулю и решить относительно
, приравнять её нулю и решить относительно 



