
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возбуждения электрических машин с учётом насыщенияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Процессы в цепи возбуждения электрических машины без учёта влияния реакции якоря, потоков рассеяния и вихревых токов можно описать следующими дифференциальными уравнениями: UВ = IВ×RВ + WВ
ФВ = ¦(IВ), (4.2)
где UВ, IВ - соответственно напряжение и ток возбуждения; RВ - суммарное сопротивление цепи возбуждения с учётом силовой цепи возбудителя; WВ - суммарное число витков обмотки возбуждения; ФВ - поток возбуждения; ¦(IВ) - нелинейная зависимость, не имеющая аналитического выражения, называемая кривой намагничивания электрической машины. На рис. 4.1, приведена обобщённая кривая намагничивания двигателя в относительных единицах.
Рис. 4.1
Вводим оператор дифференцирования в уравнение (4.1)
UВ = IВ×RВ + WВ×ФВ×р. (4.1) Отсюда ФВ =
Преобразуем выражение за скобками в (4.2) к виду
где КВН =
Соответственно коэффициент и электромагнитная постоянная времени цепи возбуждения электрической машины для спрямлённой характеристики намагничивания рис. 4.1 (прямая 2).
Тогда выражение (4.2) преобразуется к виду
ФВ =
На основе (4.2) и обратной кривой намагничивания IВ = ¦1(ФВ) нелинейная цепь возбуждения может быть представлена структурной схемой вида (рис. 4.2).
Рис. 4.2
Если провести линейную аппроксимацию кривой намагничивания для какого-либо конкретного значения потока ФВ0, то структурная схема на рис. 4.2 может быть преобразована к виду (рис. 4.3).
Рис. 4.3
Здесь Кi =
Рис. 4.4
Здесь КВ = Параметры исследуемой цепи возбуждения по вариантам приведены в таблице 4.1.
Таблица 4.1.
Внимание! До того, как приступить к выполнению лабораторной работы, необходимо рассчитать реальную кривую намагничивания двигателя для своего варианта, используя для этого рис. 4.1 и номинальные данные из таблицы. Кривая намагничивания моделируется с помощью блока Look-Up Table. После этого рассчитать параметры и реализовать цифровую модель в соответствии со структурной схемой на рис. 4.2. В отчёте по лабораторной работе необходимо:
1) проанализировать переходные процессы в цепи возбуждения, обусловленные изменением напряжения возбуждения DUВ = +0.1UВН при условии, что к обмотке возбуждения уже приложено напряжение UВ0 = 0.3UВН, 0.6UВН и 0.9UВН. Для того, чтобы исключить переходные процессы, связанные с приложением к обмотке возбуждения начального напряжения UВ0, необходимо в интегрирующем звене на модели задать начальное значение потока возбуждения, рассчитанное для этого режима с учётом кривой намагничивания; 2) для трех начальных значений протока возбуждения построить частотные характеристики (ЛАЧХ и ЛФЧХ), входной сигнал для частотной характеристики 3) по полученным кривым переходных процессов рассчитать значения КВ и ТВ для каждого режима; 4) построить зависимости КВ и ТВ от величины 5) сделать выводы по полученным результатам. Лабораторная работа № 5 Исследование переходных процессов в двигателе Постоянного тока при однозонном Регулировании скорости
Структурная схема двигателя постоянного тока при постоянном потоке возбуждения наиболее часто представляется в виде, изображённом на рис. 5.1.
Рис. 5.1
Здесь RЭ, ТЭ - эквивалентное сопротивление и постоянная времени якорной цепи двигателя; КФН - коэффициент двигателя;
ТМ =
Исходные параметры по структурной схеме для каждого варианта приведены в табл. 5.1.
Таблица 5.1
Для всех вариантов ТЭ = 0.03 с. В отчёте по лабораторной работе на основе реализованной модели необходимо рассчитать и проанализировать переходные процессы UЯ(t), IЯ(t), w(t) в следующих режимах:
1) разгон и торможение двигателя на холостом ходу при изменении напряжения якоря в соответствии с рис. 5.2.; 2) для данной структурной схемы построить частотные характеристики (ЛАЧХ и ЛФЧХ) для трёх случаев: а) входной сигнал для частотной характеристики б) входной сигнал для частотной характеристики в) входной сигнал для частотной характеристики 3) разгон и торможение двигателя при приложении IС = IН: а) активного статического момента (тока) в интервале времени 0 ¸ t5; б) реактивного статического момента, появляющегося при w ¹ 0, (на модели реализуется с помощью релейного элемента РЭ с уровнем ограничения, равным IC = IН); в) статического момента, прикладываемого в период разгона двигателя (t = t1) и снимаемого в период торможения (t = t4); 4) приложения скачка напряжения якоря DUЯ = 0.1UЯН при UЯ0 = (0.5 ¸ 0.8)UЯН = const; 5) приложение IC = IЯН при UЯ0 = (0.5 ¸ 0.8)UЯН.
Внимание! В двух последних режимах для исключения переходных процессов, вызванных начальным изменением напряжения якоря при UЯ0, необходимо в звене, моделирующем электромеханическую инерцию двигателя, задать начальное значение скорости w0 =
Величины и характер изменения UЯ(t) и IС(t) для каждого варианта представлены на рис. 5.2 и в табл. 5.2.
Рис. 5.2
Таблица 5.2
В отчёте по лабораторной работе необходимо: 1) проанализировать переходные процессы для всех, указанных выше, режимов; 2) проанализировать полученные частотные характеристики для всех, указанных выше, режимов 3) установить влияние на характер переходных процессов и установившихся режимов: - изменения напряжения якоря; - характера статического момента; 4) сделать необходимые выводы по полученным результатам.
Лабораторная работа № 6
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.74.217 (0.008 с.) |

 ; (4.1)
; (4.1)
 . (4.2)
. (4.2) =
=  =
=  ,
, и ТВН =
и ТВН = 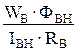 .
.

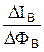 , причём DIВ и DФВ относительно небольшие приращения тока и потока возбуждения, полученные по кривой намагничивания в окрестности аппроксимируемой точки IВ0 (см. рис. 4.1). После эквивалентных преобразований структурная схема на рис. 4.3 может быть представлена на рис. 4.4.
, причём DIВ и DФВ относительно небольшие приращения тока и потока возбуждения, полученные по кривой намагничивания в окрестности аппроксимируемой точки IВ0 (см. рис. 4.1). После эквивалентных преобразований структурная схема на рис. 4.3 может быть представлена на рис. 4.4.
 и ТВ =
и ТВ = 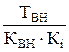 соответственно коэффициент и электромагнитная постоянная времени цепи возбуждения для выбранной точки аппроксимации. Очевидно, что по мере возрастания тока возбуждения растёт и величина коэффициента Кi, а это, в свою очередь, снижает значения КВ и ТВ по мере насыщения магнитной системы электрической машины.
соответственно коэффициент и электромагнитная постоянная времени цепи возбуждения для выбранной точки аппроксимации. Очевидно, что по мере возрастания тока возбуждения растёт и величина коэффициента Кi, а это, в свою очередь, снижает значения КВ и ТВ по мере насыщения магнитной системы электрической машины.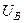 , выходной
, выходной  .
. ;
;
 - электромеханическая постоянная времени электропривода, а JS - суммарный момент инерции электропривода.
- электромеханическая постоянная времени электропривода, а JS - суммарный момент инерции электропривода. , выходной
, выходной  ;
; , выходной
, выходной  , выходной
, выходной  .
.



