Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деревянные арки. Виды арок и области применения. Способы восприятия распора. Устройство опорных узлов. Расчет арок.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ответ: Арки относятся к плоским распорным несущим конструкциям. Деревянные арки являются в настоящее время наиболее распространенными основными несущими конструкции деревянных покрытий зданий различного назначения. Их изготовляют путем склеивания надежными синтетическими клеями гнутых и прямых клеедеревянных элементов значительных длин и сечений требуемой несущей способности. Клееные дощатые арки - наиболее эффективный вид несущих деревянных конструкций, особенно при круговом или стрельчатом очертании. Клееные фанерные арки - применяют реже из-за трудоемкости их изготовления и дефицитности высококачественной фанеры. Клееные деревянные арки рекомендуется применять при пролетах от 12 до 60 м. Конструкции клеедеревянных арок являются простыми, состоят из минимального числа элементов. Существенное значение имеет также архитектурная выразительность деревянных арочных покрытий. К достоинствам деревянных арок из клеедеревянных элементов следует также отнести их повышенный предел огнестойкости и достаточно длительное сопротивление загниванию и разрушению в химически агрессивных средах при условии конструирования узлов на деревянных или стеклопластиковых нагелях. Как и клееные балки, арки образуются склеиванием досок. Криволинейные арки по статической работе более выгодны, чем прямолинейные треугольные, однако их изготовление более трудоемко. Дощатоклееные деревянные арки представляют собой пакет склееных по пласти гнутых слоев. Поперечное сечение арок рекомендуется принимать прямоугольным и постоянным по всей длине. При больших пролетах целесообразно применять арки переменного по высоте сечения, принятого с учетом изменения момента по длине. Другие виды сечений допускается применять при надлежащем технико-экономическом обосновании. Клееные арки обычно изготавливают с постоянным по длине арки прямоугольным поперечным сечением с h/b≤ 8. Сечения арок могут быть армированными. Арки могут применяться в зданиях различного назначения с утепленными или неутепленными ограждающими конструкциями из панелей или листовых материалов. 1.Классификация арок Деревянные арки разделяются: I. По статической схеме: 1. Трехшарнирные арки. Имеют два опорных и один коньковый (ключевой) шарнир. Являются наиболее распространенными. Они статически определимы, и усилия в их сечениях не зависят от осадок опор и деформаций затяжек. Наличие конькового шарнира позволяет предусматривать в нем монтажный стык и перевозить арки к месту установки в виде полуарок (рис. 1.1, а); 2. Двухшарнирные арки. Имеют только два опорных шарнира. Двухшарнирные арки применяются реже. Усилия в их сечениях зависят от осадок опор, деформаций затяжек и они не могут делиться простыми шарнирными узлами на более транспортабельные элементы, поэтому их пролеты ограничены (рис. 1.1, б); 3. Бесшарнирные арки (рис. 1.1, в). II. По особенностям опирания на опоры: 1. С затяжками Арки с затяжками сложнее по конструкции. Опоры рассчитываются только на вертикальные опорные давления (рис. 1.1, г); 2. Без затяжек. Арки без затяжек опираются на фундаменты или стеновые несущие конструкции и являются наиболее простыми. Опоры должны рассчитываться на вертикальные и на горизонтальные (распор) опорные давления (рис. 1.1, д). III. По профилю (очертанию): Пологие - двухшарнирные и трехшарнирные арки кругового очертания. Стрела подъема принимается f ≤1/6L, при соответствующем технико-экономическом обосновании может быть уменьшена до 1/7-1/8L.Высоту поперечного сечения арок рекомендуется назначать от 1/20 до1/30L; 2. Высокие - стрельчатые трехшарнирные арки из элементов кругового очертания. Стрела подъема принимается f ≤1/3L-2/3L. Высоту поперечного сечения арок рекомендуется назначать от 1/30 до1/50L; 3. Стрельчатые арки. Состоят из двух полуарок, оси которых располагаются на двух одинаковых частях окружности, стыкующихся под углом в коньковом шарнире, как правило, без затяжек. Расчетная схема трехшарнирная. Стрела подъема принимается f ≤1/3L-1/3L. Высоту поперечного сечения арок рекомендуется назначать от 1/30 до1/40L (рис. 1.1, е); 4. Треугольные арки.
IV. По форме сечения: 1. Прямоугольное из склеенных досок (рис. 1.1, з); 2. Тавровое (рис. 1.1, и); 3. Коробчатое (рис. 1.1, к); 4. Армированное стальными стержнями.
Рис. 1.1 Клеедеревянные арки: а – трехшарнирные, б - двухшарнирные, в - безшарнирные, г – с затяжками, д - без затяжки, е – стрельчатые, ж – треугольные, з – прямоугольное сечение, и – двутавровое сечение, к – коробчатое сечение.
Расчет арок производится по правилам строительной механики, причем распор пологих двухшарнирных арок при стреле подъема не более 1/4 пролета разрешается определять в предположении наличия шарнира в ключе. Нагрузки, действующие на арку, могут быть распределенными и сосредоточенными. Постоянную равномерную нагрузку g от массы покрытия и самой арки определяют с учетом шага арок. Она обычно условно считается в запас прочности, равномерно распределенной по длине пролета, для чего ее фактическое значение умножают на отношение длины арки к ее пролету S/l. Массой арки можно задаться предварительно с использованием коэффициентов собственной массы kсв=2…4, и определить его в зависимости от массы покрытия gn, снега p и других нагрузок из выражения
Снеговую нагрузку р определяют по нормам нагрузок и воздействий, условно равномерно распределенную по длине пролета покрытия. При расчете сегментных арок при f/l≥1/8 нужно учитывать также распределение снеговой нагрузки по треугольным эпюрам при значении коэффициента перехода в ключе 0, близ опор – от 1.6 до 2.2 с одной стороны и от 0.8 до 1.1 – с другой. Стрельчатые арки при определении снеговых нагрузок могут условно считаться треугольными. Ветровую нагрузку q определяют по нормам нагрузок и воздействий с учетом шага арок и считают приложенной нормально к поверхности покрытия. При этом для упрощения расчета криволинейные эпюры этой нагрузки можно заменять прямолинейными нормальными к хордам полуарок. При стрельчатых арках они условно могут считаться треугольными, и нагрузка распределится нормально к хордам полуарок. Сосредоточенные, временные нагрузки Р включают в себя массу подвесного оборудования и временных нагрузок на нем. Геометрический расчет арки заключается в определении всех размеров, углов и их тригонометрических функций полуарки, необходимых для дальнейших расчетов. Исходными данными при этом являются пролет l, высота f, а в стрельчатых арках также радиус полуарки r или ее высота f.
Рисунок 8 – Геометрическая и расчетная схема арки В стрельчатых арках определяют угол наклона α и длину l хорды, центральный угол φ и длину S/2 полуарки, координаты центра a и b, угол наклона опорного радиуса φ0 и уравнение дуги левой полуарки Статический расчет Опорные реакции трехшарнирной арки состоят из вертикальных и горизонтальных составляющих. Вертикальные реакции Ra и Rb определяют как в однопролетной свободно опертой балке из условия равенства нулю моментов в опорных шарнирах. Горизонтальные реакции (распор) Ha и Hb определяют из условия равенства нулю моментов в коньковом шарнире. Определение реакций и усилий удобно производить в сечениях только одной левой полуарки в следующем порядке: Изгибающие моменты следует определять во всех сечениях и иллюстрировать эпюрами. Продольные и поперечные силы можно определять только в сечениях у шарниров, где они достигают максимальных величин и необходимы для расчетов узлов. Необходимо также определять продольную силу в месте действия максимального изгибающего момента при таком же сочетании нагрузок. Усилия от двустороннего снега и собственной массы определяют путем суммирования усилий от односторонних нагрузок. Полученные результаты сводят в таблицу усилий, по которой затем определяют максимальные расчетные усилия при основных наиболее не выгодных сочетаниях нагрузок. ^ Рисунок 9 – Силовые воздействия в опорном узле арки
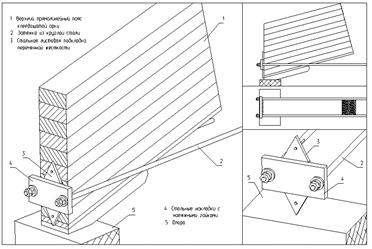
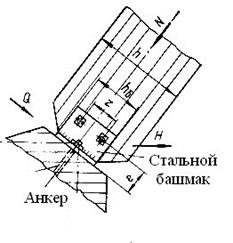
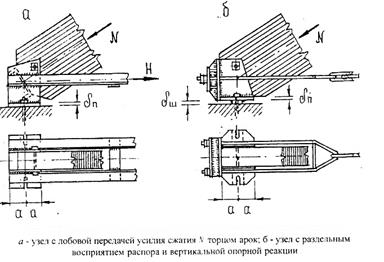
Наибольшие продольные силы возникают в сечениях близ опор, а наибольшие поперечные силы – в сечениях близ шарниров. Узлы сегментных и стрельчатых арок, в которых действуют изгибающие моменты разного знака и незначительные поперечные силы, центрируются по осям полуарок, а опорный лист башмака перпендикулярен им. Узлы треугольных арок, в которых действуют в основном положительные моменты и значительные поперечные силы, центрируются по расчетным осям, расположенным с эксцентриситетом относительно осей полуарок, а опорный башмак перпендикулярен равнодействующей вертикальной и горизонтальной опорных реакций. ^ Рисунок 11 – Опорная площадка, воспринимающая опорную реакцию без сдвига
Болты крепления полуарки к фасонкам рассчитывают на действие максимальной поперечной силы Q, как симметрично изгибаемые, двухсрезные. На эту же силу рассчитываются анкерные болты на срез и смятие. Бетон фундамента рассчитывается на смятие от силы Nсм. Опорный лист башмака работает на изгиб от действия равномерного давления лобового торца полуарки. ^ Рисунок 12 – Опорный узел с шарниром
^ Опорные узлы арок с затяжками ^ Рисунок 13 – Опорный узел с металлической затяжкой Опорный узел сегментной арки с деревянной затяжкой на болтах:
Опорный лист в арках с затяжками располагается горизонтально, поэтому арки ставятся на горизонтальную поверхность опор, на которые не действует распор. Вертикальные фасонки могут опираться на опорный лист или опорный лист может размещаться между фасонками. При опирании на бетон опорный лист удлиняют за пределы фасонок для крепления анкеров, а при опирании на деревянную стойку фасонки опирают ниже опорного листа для крепления их к стойке болтами. Между фасонками располагается упорная диафрагма. Наклон диафрагмы и центрирование узла производятся по тем же соображениям, что и в узлах арок без затяжек. Металлическую затяжку приваривают к фасонкам, деревянную распологают между фасонками и крепят к ним болтами.
Коньковые узлы сплошных арок малых и средних пролетов решаются в виде прямых или наклонных лобовых упоров со стальными креплениями или деревянными накладками на болтах. Сегментные и стрельчатые клееные арки центрируются в этих узлах по осям полуарок, а треугольные – с эксцентриситетами (с той же целью, что и в опорных узлах).
^ Рисунок 16 – Коньковый узел треугольной арки
Рисунок 17 – Коньковый узел сегментной арки
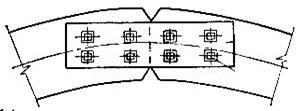
Стыки элементов арок.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 4490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.58 (0.009 с.) |

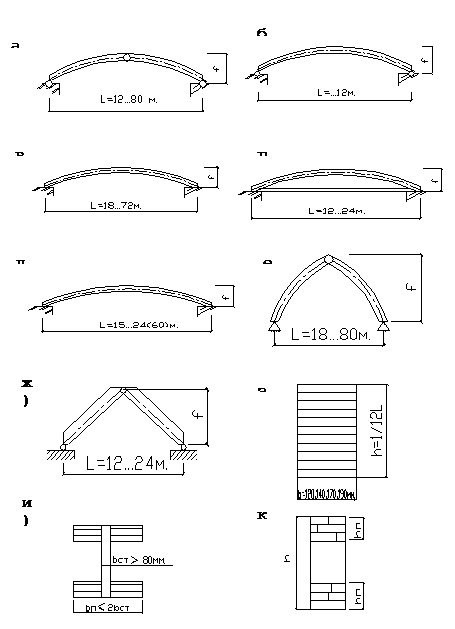 Могут быть только трехшарнирными с затяжками или без них. Проще в изготовлении и монтаже. Стрела подъема принимается f ≤1/2L-1/5L. Высоту поперечного сечения арок рекомендуется назначать от 1/20 до1/30L (рис. 1.1, ж).
Могут быть только трехшарнирными с затяжками или без них. Проще в изготовлении и монтаже. Стрела подъема принимается f ≤1/2L-1/5L. Высоту поперечного сечения арок рекомендуется назначать от 1/20 до1/30L (рис. 1.1, ж).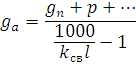
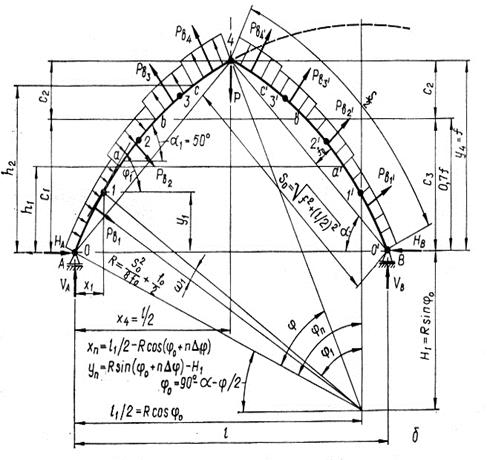 По этим данным в треугольных арках определяют длину S/2 и угол наклона полуарки α. В сегментных арках определяют радиус
По этим данным в треугольных арках определяют длину S/2 и угол наклона полуарки α. В сегментных арках определяют радиус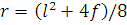 ,
,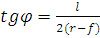 и длину дуги
и длину дуги 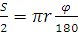 полуарки и находят уравнение дуги в координатах с центром в левой опоре
полуарки и находят уравнение дуги в координатах с центром в левой опоре 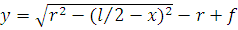
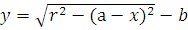 . Затем половину пролета арки делят на четное число, но не менее шести равных частей и в этих сечениях определяют координаты х и у, углы наклона касательных α и их тригонометрические функции.
. Затем половину пролета арки делят на четное число, но не менее шести равных частей и в этих сечениях определяют координаты х и у, углы наклона касательных α и их тригонометрические функции.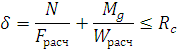
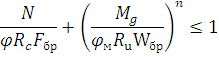
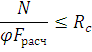
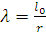 .
. Затяжки и подвески арок работают и рассчитываются на растяжение.
Затяжки и подвески арок работают и рассчитываются на растяжение.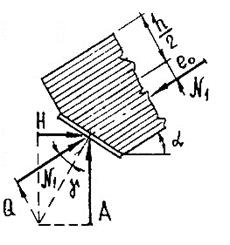
 Расчет опорного узла заключается в расчете торца полуарки на смятие от действия максимальной сжимающей силы Nсм. В сегментных и стрельчатых арках она равна максимальной продольной силе N и действует вдоль волокон. В треугольных арках она равна равнодействующей опорных усилий
Расчет опорного узла заключается в расчете торца полуарки на смятие от действия максимальной сжимающей силы Nсм. В сегментных и стрельчатых арках она равна максимальной продольной силе N и действует вдоль волокон. В треугольных арках она равна равнодействующей опорных усилий
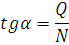
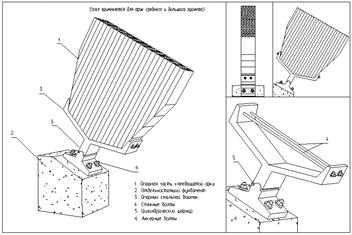
 Опорные узлы клееных арок, работающих в условиях химической агрессии, могут быть выполнены при помощи стержней, одним концом вклеенных в конец полуарки, а другим – заанкерованных в фундамент.
Опорные узлы клееных арок, работающих в условиях химической агрессии, могут быть выполнены при помощи стержней, одним концом вклеенных в конец полуарки, а другим – заанкерованных в фундамент.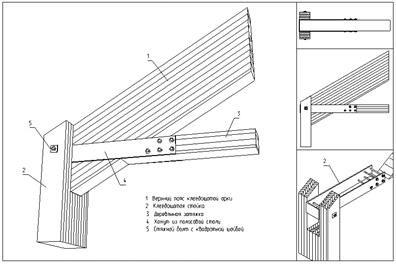
 ;
;