
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колмогорову, место моделирования в управлении организацией.Содержание книги
Поиск на нашем сайте
Моделирование – это концепция, которой уделено много внимания в нашем обсуждении. Наиболее заметный и, возможно, наиболее значительный вклад школы научного управления заключается в разработке моделей, позволяющих принимать объективные решения в ситуациях, слишком сложных для простой причинно-следственной оценки альтернатив. Многие из таких моделей настолько сложны, что не всякий средний руководитель в состоянии воспользоваться ими самостоятельно. Однако отсутствие основательного представления о моделях может привести руководителя к методу проб и ошибок и принятию необдуманных решений вместо применения проверенных методов.
В процессе разработки УР мы имеем возможность накапливать ситуации и решения, принятые по ним. Т.о. сформировать базу или банк ситуаций и решений (БСР). Т.о. появляется возможность при выходе на аналогичную ситуацию при разработке УР использовать уже имеющиеся решения в БСР. Задачи м/б: оптимизационные и прямого счета. При одной модели будет столько алгоритмов, сколько существует вариантов решений. Задача прямого счета не м/б в нескольких вариантах. Чем более конкретна цель тем меньше степень неопределенности и больше возможностей разработать действенное Ур. Информация, собираемая об объекте, привязана к текущему моменту (как статич. информация должна быть привязана к моменту времени, так и динамика четко привязана к определенному моменту времени). Задачи вариантно-оптимизационные требуют ограниченных критериев. Если задача учетная, то альтернатив быть не может в учете того, что мы получили. Модель – условный образ объекта или системы, для которой разрабатывается решение, представляющее собой взоимосвязь элементов системы или объектов, являющихся основными с точки зрения решаемой задачи в данном случае мы говорим о 2-х понятиях: изоморфизм(соответствие) и гомоморфизм (сходство).
Реальная ситуация и образ – гомоморфизм. Образ и модель изоморфны. Д/б 3 ключевых набора при пострении модели:
Для того, чтобы представить объект с позиции решаемой задачи, нужно: 1) выбирать основные элементы, каждый элемент образа имеет элемент тождественный ему в системе, но не каждый элемент системы присутствует в образе, элементов в реальной системе больше, чем количество элементов образа. 2) имея образ, можно представить элемент и взаимосвязи в модели: они адекватны и соответственны. Риски: Модель может не учесть существенные взаимосвязи, которые формируются на базе существенных с точки зрения задач. В связи с реальной возможностью значительного огрубления моделируемого объекта или системы при отборе существенных элементов и пренебрежение несущественными элементами могут нарушиться связи элементов, и модель не будет удовлетворять требуемого решения задачи. В этом случае необходима корректировка модели, связанная с уточнением как состава элементов, так и их взаимосвязи. И так же итерации этих корректировок могут неоднократно повторяться, пока мы не получим такой вариант модели, который нас устроит. Объектами корректировки м/б:
50. Схема построения модели, содержание основных процедур. При разработке управленческого решения, прежде всего, необходимо осознание самой задачи. Далее необходимо определить, к какому классу относится решаемая задача: прямого счета, вариантная, оптимизационная. Если задача оптимизационная, необходимо установить, нужен выход на чистый математический оптимум или достаточно получить допустимое решение. Следует также иметь в виду, что для решения ряда задач в арсенале математического программирования и другого специального инструментария уже есть готовые модели. Поэтому нет необходимости разрабатывать новую модель, нужно выбрать наиболее подходящую и адаптировать ее к своей задаче. Например, решение задач, связанных с разработкой оптимальных графиков НИОКР; с разработкой производственных программ для вновь созданных производственных подразделений на определенные периоды времени, при этом программы формируются по критерию максимизации (минимизации) заданного показателя – объема выполняемых работ, количества (стоимости) выпускаемой продукции, величины издержек, используемых материальных ресурсов, численности персонала, затрат на подготовку и переподготовку кадров и т.п. Пусть требуется максимизировать (минимизировать) функцию
F (x) ® (a1*x1 + a2*x2 + …+ai*xi +… + an*xn) ® max (min), где a1, a2, …, an – удельные призначные характеристики (показатели) i – х элементов, формирующих величину функции (Пi). Представим исходную функцию в следующем общем виде:
где Пi – призначная характеристика i –ой номенклатурной позиции (элемента); хi – искомая переменная величина (количество) i –ой позиции. Такая запись представляет собой критериальную функцию решения задачи. Ограничительными условиями могут выступать имеющиеся ресурсы (трудовые, материальные, финансовые и другие), а также ограничения на величину самой функции ??? Таким образом, рассматриваемая ситуация вписывается в уже известные модели, и проектанту (студенту) нет необходимости самостоятельно разрабатывать такого рода модель. Рассмотрим следующую ситуацию: выбрать претендента (кандидатуру) на включение в состав временного трудового коллектива для разработки крупного инновационного проекта, который бы в наибольшей степени соответствовал требованиям, предъявляемым организацией к претенденту. Готовой модели для решения этой задачи нет, поэтому студент вынужден самостоятельно ее разрабатывать. Рассмотрим основные этапы построения модели. 1 этап. Формулирование решаемой задачи. 2 этап. Определение типа задачи (оптим, прямого сч) 3 этап. Определение объекта моделирования. В качестве такого объекта может выступать процесс работы над инновационным проектом, претендент (кандидат) на включение в коллектив, выполняемая научно-исследовательская работа, формируемый график выпуска продукции, поиск вариантов сокращения транспортного маршрута для снижения величины транспортных расходов и т.п. 4 этап. Выявление элементов моделируемого объекта и их характеристика. 5 этап. Отбор из числа этих элементов наиболее существенных для решения данной конкретной задачи. 6 этап. Формирование набора показателей, характеризующих каждый из выбранных в пункте 4 элементов объекта. 7 этап. Описание в общем виде объекта моделирования с позиции решаемой задачи. Этот этап можно реализовать в два приёма: 1) с помощью математических символов в неявном виде 2) С учетом постановки задачи описать объект моделирования, увязав указанные выше показатели с помощью выявленных расчётных формул.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.93.61 (0.007 с.) |



 F (x) ® max (min)
F (x) ® max (min)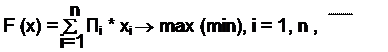
 описываются взаимосвязи и взаимозависимости выбранных элементов объекта, то есть формируется набор показателей x1, x2,…,xn (где x1, x2,…,xn — показатели, характеризующие наиболее существенные элементы объекта), затем следует представить расчетные формулы этих показателей. Источником получения формул может быть прежде всего специальная литература. Если готовых формул найти не удается, то проектант может вывести их самостоятельно, комбинируя информацию из литературных источников, применяя специальные приемы и методы математической статистики, теории вероятностей и т.д., а также используя свои знания и навыки в области моделирования.
описываются взаимосвязи и взаимозависимости выбранных элементов объекта, то есть формируется набор показателей x1, x2,…,xn (где x1, x2,…,xn — показатели, характеризующие наиболее существенные элементы объекта), затем следует представить расчетные формулы этих показателей. Источником получения формул может быть прежде всего специальная литература. Если готовых формул найти не удается, то проектант может вывести их самостоятельно, комбинируя информацию из литературных источников, применяя специальные приемы и методы математической статистики, теории вероятностей и т.д., а также используя свои знания и навыки в области моделирования.


