Структура лфд. Принцип действия лавинного фотодиода. Распределение электрического поля. Коэффициент лавинного умножения. Шумы фотодиодов.

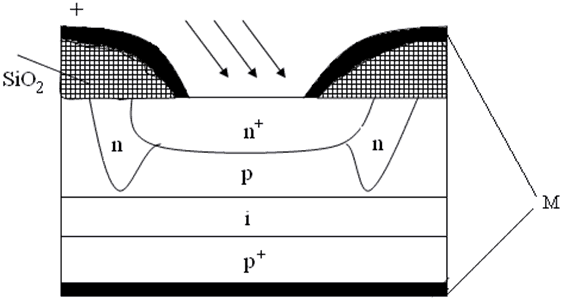
Предельная чувствительность p-i-n-фотодиода определяется хаотическими флуктуациями напряжения и тока на выходе, которые имеются как в присутствии оптического сигнала, так и без него. В случае p-i-n-диода – это тепловой и дробовой шум и шум темнового тока. Значительного увеличения пороговой чувствительности можно добиться в лавинных фотодиодах (ЛФД), работа которых основана на лавинном умножении носителей, так как в этом случае возникает внутреннее усиление. Конечно, при этом умножатся шумы диода, но суммарный эффект останется положительным, Такое умножение можно получить в лавинном процессе при высоких значениях электрического поля в лавинном фотодиоде. Структура продольного сечения ЛФД показан на рисунке 5.9.

Рисунок 5.9 – Структура продольного сечения ЛФД

Особенностью ЛФД является наличие защитного кольца в виде глубоко диффундированной n-области на краю n⁺-p-перехода. Защитное кольцо уменьшает ток утечки вблизи краёв перехода и предотвращает низковольтный пробой.
Структура материалов, образующих ЛФД, его топологическая схема и технология изготовления обеспечивают работоспособность устройства в таком режиме. Процесс образования носителей в ЛФД, включение его в цепь, возникновение фототока и распределение напряженности электрического поля показаны на рисунке 5.10.

Рисунок 5.10 – Процесс образования носителей тока в ЛФД, возникновение фототока и распределение электрического поля в структуре

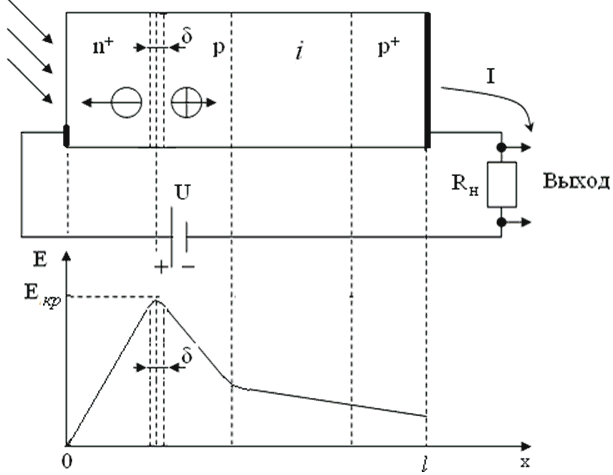
Допустим, что смещение достигает величины, при которой в запирающем p-n⁺-слое электрическое поле превысит значение критической напряженности E_кр. Тогда образованные фотонами первичные электроны и дырки получают энергию, достаточную для того, чтобы посредством ударной ионизации образовывать новые пары носителей.
Это умножение носителей происходит в довольно узкой области δ вблизи пика электрического поля. Первичные электроны и дырки на длине свободного пробега в кристаллической решётке получают от электрического поля кинетическую энергию, равную ширине запрещённой зоны. Вторичные носители заряда, в свою очередь, способствуют ударной ионизации и образованию новых пар. Таким образом, первоначально слабый фототок возрастает лавинообразно. Рассмотренный ЛФД работает при напряжениях смещения U больше критического напряжения U_кр, соответствующего критической напряжённости E_кр:

U > U_кр

В отличие от p-i-n - ФД у ЛФД поглощение фотона приводит к появлению не одной электронно-дырочной пары, а М пар. Величина М называется коэффициентом лавинного умножения. Поэтому увеличение тока можно охарактеризовать с помощью этого коэффициента.
Для обычного р-n-перехода коэффициент лавинного умножения, равный кратности увеличения фототока, определяется по формуле:

где U – внешнее смещение;
U_кр – критическое напряжение перехода;
γ = 1,5 – 4 для кремния и γ = 2,5 – 9 для германия.
Если бы процесс лавинного умножения был определенным, то каждая первичная электронно-дырочная пара создавала М вторичных пар. На самом деле в реальном ЛФД умножение не определённое, то есть каждая первичная пара порождает случайное число вторичных пар, среднее число которых может быть равно <М>, однако мгновенное изменения М могут быть большими. Тогда лавинный ток будет:

Величина имеет порядок 10–100. Конструктивно ЛФД существенно сложней p-i-n - ФД. Кроме того, для создания условий лавинообразного размножения носителей требуется существенно увеличить размеры обеднённой области. При больших U сильные токи приводят к разогреву полупроводника, что увеличивает темновой ток и уменьшает фототок (электрический пробой переходит в тепловой). Проигрывает ЛФД и по шумовым характеристикам. Это объясняется тем, что процесс образования лавины носит случайный характер и является дополнительным источником шума. Из-за сильной зависимости M(U) использование ЛФД затрудняется необходимостью применения высокостабильного напряжения. Однако ЛФД значительно превосходит p-i-n - ФД по чувствительности.