
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экспериментальные и расчетные данныеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где: S - площадь поперечного сечения цилиндра. Результаты заносят в таблицу 2.1. 3. По полученным значениям перепада давления ΔР в слое зернистого материала высотой h и скорости воздуха w в сечении цилиндра, в координатах ΔР – w строят график зависимости ΔР = f (w). 4. Определяют экспериментальное значение скорости начала псевдоожижения wкрэксп. Для этого на графике зависимости ΔР = f (w) обозначают точку, соответствующую моменту перехода слоя в псевдоожиженное состояние. Абсцисса этой точки представляет экспериментальное значение скорости начала псевдоожижения wкрэксп. Результаты заносят в таблицу 2.1. 5. Определяют кажущуюся (насыпную) плотность слоя зернистого материала rн:
Результаты заносят в таблицу 2.1. 6. По уравнению (2.3) определяют порозность e слоя зернистого материала e. Результаты заносят в таблицу 2.1. 7. Используя уравнения (2.6) и (2.7) определяют расчетное значение скорости начала псевдоожижения wкp. Результаты заносят в таблицу 2.1. 7. Определяют относительное отклонение экспериментального значения скорости начала псевдоожижения wкрэксп от расчетного значения wкр:
Результаты заносят в таблицу 2.1.
Вопросы для самоконтроля 1. Определение «кипящего» слоя зернистого материала. 2. Порядок экспериментального определения скорости начала псевдоожижения слоя зернистого материала. 3. Алгоритм определения скорости начала псевдоожижения по формулам, рассматриваемым в теоретической части лабораторной работы. 4. Параметры, влияющие на величину скорости начала псевдоожижения слоя зернистого материала. 5. Режимы фильтрации потока газа через неподвижный слой зернистого материала. 6. Влияние скорости потока среды на порозность и плотность псевдоожиженного слоя. 7. Преимущества и недостатки «кипящего» слоя по сравнению с неподвижным слоем зернистого материала. Лабораторная работа № 3 ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ВИТАНИЯ ЧАСТИЦ РАЗЛИЧНОЙ ФОРМЫ В ПОТОКЕ ГАЗА Цели лабораторной работы · экспериментальное определение скоростей витания частиц различной формы в потоке воздуха; · сравнение экспериментальных данных с расчетными.
Теоретические основы Скоростью витания называется скорость потока среды, при которой частицы слоя зернистого материала переходят во взвешенное состояние, т.е. величина подъемной силы потока, действующей на отдельную частицу, уравновешивает её вес. Скорость витания служит верхним пределом существования псевдоожиженного слоя зернистого материала данного гранулометрического состава. Если скорость потока превышает скорость витания, частицы зернистого материала, начиная с наиболее мелких, начинают выноситься из слоя, изменяя тем самым гранулометрический состав материала. Для расчета скоростей витания частиц наибольшее распространение получило критериальное уравнение Тоддеса О.М., Горошко В,Д. и Розенбаума Р.Б., справедливое для всех режимов обтекания частицы потоком: ламинарного, переходного и турбулентного:
где Re и Ar - критерии Рейнольдса и Архимеда соответственно; e - доля свободного сечения в месте нахождения частицы от общего свободного сечения или порозность слоя. Критерий Архимеда Ar рассчитывается по уравнению:
где g - ускорение силы тяжести; d – диаметр частицы; rч - плотность материала частицы; r - плотность потока; m - динамическая вязкость потока.
Для турбулентного режима обтекания частицы потоком значения критерия Архимеда сравнительно высоки. Учитывая это, первым слагаемым знаменателя уравнения (3.) можно пренебречь:
или
С другой стороны мы можем определить критерий Рейнольдса как:
где Wв - скорость витания частицы. Решая совместно уравнения (3.4) и (3.5), получим выражение для определения скорости витания частиц сферической формы при турбулентном режиме обтекания потоком:
Рассматривая процесс витания частиц несферической формы для их характеристики пользуются понятием эквивалентного диаметра. Под эквивалентным диаметром подразумевают диаметр сферической частицы из материала той же плотности, которая в восходящем потоке среды имеет ту же скорость витания, что и частица несферической формы. Из уравнения (3.6) можно получить выражение для расчета эквивалентного диаметра частиц несферической формы, предварительно экспериментально определив их скорость витания:
Скорость витания так же можно найти из условия равновесия сил действующих на частицу во взвешенном состоянии. Рассмотрим одиночную частицу зернистого материала находящуюся в восходящем потоке среды (рис. 3.1). Подъемная сила потока R, действующая на частицу, определяется скоростью потока W0 в сечении каналов, не занятых частицами. Подъемная сила равна произведению перепада давления потока ΔP на площадь проекции S0 частицы на плоскость, перпендикулярную направлению движения потока.
где: ξ - коэффициент гидравлического сопротивления при обтекании частицы потоком; ρ - плотность потока; W0 - скорость потока среды в сечении, не занятом частицами.
Рис. 3.1. Частица в восходящем потоке среды Для частиц, площадь проекции S0 которых мала по сравнению с сечением каналов не занятых частицами, скорость W0 можно считать равной скорости потока в свободном сечении W, т.е. W ≈ W0 . В момент перехода частицы слоя во взвешенное состояние подъёмная сила потока R становиться равной разности силы тяжести G и выталкивающей силы потока G’, действующих на частицу.
где g - ускорение силы тяжести; Vч – обем частицы; rч – плотность материала частицы; r – плотность среды. Объединив уравнения (3.8) и (3.9), получим:
Для частицы сферической формы диаметром d уравнение (3.10) примет вид:
Выразим скорость витания:
В данной лабораторной работе режим обтекания частиц потоком среды является турбулентным. Для турбулентного режима коэффициент гидравлического сопротивления ξ можно определить из уравнения Петиджена и Христиансена:
где j - коэффициент формы (или фактор формы) частицы. Коэффициент формы j (или фактор формы) частицы определяется как:
где Fрш – площадь поверхности равновеликого шара, т.е. шара, объём которого равен объёму частицы; Fч - площадь поверхности частицы. Коэффициент формы j частиц геометрически правильной формы определяется аналитически. Для наиболее часто встречающихся форм частиц рассчитанные коэффициенты формы приведены в таблице П-3 приложений. Для частиц неправильной формы коэффициент j находят экспериментально. Для некоторых сыпучих материалов и насадок коэффициенты формы приведены в таблице П-4 приложений. В общем случае значение коэффициента формы лежит в пределах
Подставляя j = 1 в уранвнение (3.12) для сферических частиц при турбулентном режиме обтекания получим коэффициент гидравлического сопротивления ξ = 0,44. Подставив величину ξ = 0,44 в уравнение (3.12) получим выражение для скорости витания сферических частиц при турбулентном режиме обтекания:
Для определения скорости витания частиц несферической формы в расчетах вместо диаметра частицы d используют диаметр равновеликого шара dрш, шара, объем Vрш которого равен объему частицы Vч:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.182 (0.01 с.) |

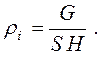 (2.10)
(2.10)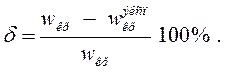 (1.11)
(1.11) (3.1)
(3.1) (3.2)
(3.2) (3.3)
(3.3) . (3.4)
. (3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) , (3.8)
, (3.8)
 (3.9)
(3.9) (3.10)
(3.10) (3.11)
(3.11) (3.12)
(3.12) (3.12)
(3.12) (3.13)
(3.13) ; для сферических частиц j = 1.
; для сферических частиц j = 1. (3.14)
(3.14) (3.15)
(3.15)


