
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Д.Н. Жедяевский, В.Д. Косьмин,Содержание книги Поиск на нашем сайте
В.А. Лукьянов, С.С. Круглов
ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ Руководство к практическим занятиям В лаборатории процессов и аппаратов Нефтегазопереработки
Москва 2012 Министерство образования и науки Российской Федерации РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА ИМЕНИ И.М. Губкина
Д.Н. Жедяевский, В.Д. Косьмин, В.А. Лукьянов, С.С. Круглов
ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ Руководство к практическим занятиям В лаборатории процессов и аппаратов нефтегазопереработки
по дисциплинам: «Процессы и аппараты нефтегазопереработки», «Процессы и аппараты химической технологии», «Процессы и аппараты защиты окружающей среды» Учебно-методическое пособие для студентов специальностей: 130603, 240401,240403,280201 и бакалавров по направлениям: 240100, 150400
Москва 2012
УДК 66.048.375
Д.Н. Жедяевский, В.Д. Косьмин, В.А. Лукьянов, С.С. Круглов Гидромеханические процессы. Руководство к практическим занятиям в лаборатории процессов и аппаратов нефтегазопереработки. - М.: РГУ нефти и газа, 2012, 76 с. Учебно-методическое пособие включает теоретические основы гидромеханических процессов: фильтрации, псевдоожижения, витания и осаждения, а так же очистки газов в циклонах, порядок проведения опытов и обработки результатов, контрольные вопросы. Учебно-методическое пособие пpедназначено для студентов специальностей 130603, 240401, 240403, 280201 и бакалавров по направлениям: 240100, 150400, изучающих курс «Процессы и аппараты нефтегазопереработки», «Процессы и аппараты химической технологии», «Процессы и аппараты защиты окружающей среды». Ил. 32, табл. 8, библ. - 6 назв.
Издание подготовлено на кафедре оборудования нефтегазопереработки.
Рецензенты: Кошелев В.Н. профессор, д.х.н.; Мельников В.Б. профессор, д.т.н.
Ó Д.Н. Жедяевский, В.Д. Косьмин, В.А. Лукьянов, С.С. Круглов Ó Издательский центр РГУ нефти и газа имени И.М. Губкина, 2012
Условные обозначения
n - кинематическая вязкость фильтрующегося потока, м2/с V – объем слоя; VП – суммарный объем поровых каналов в слое; VЧ – суммарный объем твердых частиц в слое. D - диаметра аппарата
d - диаметр твердой частицы e - порозность или доля свободного объёма xi - весовое содержание частиц диаметром di wК - скорость потока среды, отнесенная к сечению поровых каналов, м/с; H - высота слоя, м; dК - эквивалентный диаметр поровых каналов, м; r - плотность cреды, кг/м3; l - коэффициент гидравлического сопротивления wК - скорость потока среды в поровых каналах w - скорость потока среды, рассчитанная на полное сечение слоя (скорость фильтрации) m - динамическая вязкость среды, Па с; Re- число Рейнольдса Re ч - число Рейнольдса, отнесенное к диаметру частицы dрш - диаметр равновеликого по объему (весу) шара, м; j - коэффициент формы, Лабораторная работа № 1 ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ НЕПОДВИЖНОГО СЛОЯ ЗЕРНИСТОГО МАТЕРИАЛА Цели лабораторной работы · получение экспериментальной зависимости гидравлического сопротивления слоя зернистого материала от скорости воздуха и размера частиц; · сопоставление экспериментальных значений гидравлического сопротивления слоя зернистого материала с расчетными.
Теоретические основы Среда (жидкость или газ) движется через неподвижный слой зернистого материала, проходя в свободном объеме по каналам между твердыми частицами. Движение потока среды через слой сыпучего материала характеризуется периодическими сужениями и расширениями отдельных струй, на которые разделяется поток среды при входе в слой, и извилистостью пути струй по поровым каналам. Характер движения потока в слое, частота сужений и расширений отдельных струй, а также их извилистость определяются размером и шероховатостью частиц слоя зернистого материала, их фракционным составом, формой и упорядоченностью укладки, величиной объема пустот между частицами, влиянием стенок аппарата, определяемым отношением диаметра аппарата D к диаметру частицы слоя d, величиной внешней поверхности слоя в единице его объема, физическими параметрами потока (плотность, вязкость). Важнейшей характеристикой слоя является его порозность или доля свободного объёма e:
где: V – объем слоя; VП – суммарный объем поровых каналов в слое; VЧ – суммарный объем твердых частиц в слое. Если слой состоит из частиц одинакового размера, его называют монодисперсным. Зернистые материалы, в том числе катализаторы, применяемые в промышленности, состоят из частиц неодинакового размера. Слой из частиц разного размера называют полидисперсным. Размер частиц может быть определен различными способами. Для крупных частиц (более 5 мм) возможно прямое измерение штангенциркулем или микрометром. Для очень мелких частиц микроскопического порядка (менее 0,04 мм) используются косвенные методы, основанные на измерении скорости осаждения. Гранулометрический состав частицы промежуточного размера определяют просеиванием. Для этой цели используются сита с различным размером перфорации.
При проведении гидродинамических расчетов пользуются величиной среднего диаметра частиц. Так, для слоя, состоящего из шаров различных размеров с весовым содержанием xi частиц диаметром di, их средний диаметр определяется как средневзвешенную величину:
Скоростью фильтрации, или фиктивной скоростью, называют среднюю скорость потока, отнесенную к поперечному сечению аппарата. Гидравлическое сопротивление слоя зернистого материала (потеря напора в слое) может быть определено по уравнению Дарси-Вейсбаха:
где: wК - скорость потока в сечении поровых каналов; H - высота слоя; dК - эквивалентный диаметр поровых каналов; r - плотность cреды; l - коэффициент гидравлического сопротивления. Скорость потока среды в поровых каналах wК можно определить через скорость потока среды, рассчитанную на полное сечение слоя w (скорость фильтрации):
Для монодисперсного слоя, состоящего из шарообразных частиц диаметром d, эквивалентный диаметр порового канала равен
С учетом этой зависимости, уравнение (1.3) для расчета гидравлического сопротивления при движении потока в слое зернистого материала можно представить следующим образом
Коэффициент гидравлического сопротивления l может быть определен по уравнению:
где: A и B - коэффициенты, зависящие от условий взаимодействия потока и слоя твердых частиц; Re - число Рейнольдса. Число Рейнольдса Re определяется уравнением:
Заменив в уравнении (1.8) скорость потока в каналах и размер сечения канала на выражения, полученные ранее, получим
где: m - динамическая вязкость среды, Па с; Re ч - число Рейнольдса, отнесенное к диаметру частицы:
Значения плотности и вязкости среды соответствуют средней температуре потока в слое. Если подставить в уравнение (1.6) значение коэффициента гидравлического сопротивления из выражения (1.7), с учетом того, что A = 134 и B = 2,34, то получаем расчетное уравнение, предложенное Эргуном, которое хорошо описывает экспериментальные данные различных авторов по гидравлическому сопротивлению слоя зернистого материала и рекомендуется для технических расчетов:
Для слоя зернистого материала при свободной укладке расчетные значения, полученные по уравнению (1.11) совпадают с экспериментальными данными с точностью ±25%. Это уравнение не рекомендуется применять для плотных слоев с упорядоченной укладкой или засыпок с повышенной порозностью (e = 0,6÷0,98). При высоких значениях порозности перепад давления, полученный расчетным путем из уравнения Эргуна может быть значительно меньше экспериментальных данных. Согласно уравнению (1.11) падение давления представляет собой сумму двух составляющих: потеря напора на трение за счет сил вязкости (вязкостные потери) и потеря напора, обусловленная потерей кинетической энергии потока при его движении по каналам между частицами слоя. При малых значениях критерия Рейнольдса потеря напора, обусловленная потерей кинетической энергии потока, относительно мала и ею можно пренебреч. Исходя из этого уравнение (1.11) примет вид:
При больших значениях критерия Рейнольдса, наоборот, из-за относительно малой величины потери напора на трение можно учитывать только потерю напора, обусловленная потерей кинетической энергии потока. Тогда уравнение (1.11) примет вид:
Наряду с уравнением Эргуна в практике расчетов потерь напора в неподвижном слое зернистого материала используются эмпирические зависимости, приведенные в табл.1.1. Таблица 1.1
Частицы не шарообразной формы характеризуются эквивалентным диаметром:
где: dрш - диаметр равновеликого по объему (весу) шара, м; j - коэффициент формы, равный отношению поверхности равновеликого по объему шара к поверхности частицы. Некоторые значения коэффициентов формы частиц приведены в таблицах П-3 и П-4 приложений.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.214.16 (0.011 с.) |

 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4)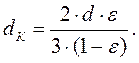 (1.5)
(1.5) (1.6)
(1.6)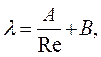 (1.7)
(1.7) (1.8)
(1.8) (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13)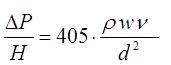








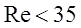


 (1.14)
(1.14)


