
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нефти и газа имени И. М. ГубкинаСодержание книги Поиск на нашем сайте
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА ИМЕНИ И.М. Губкина
Д.Н. Жедяевский, В.Д. Косьмин, В.А. Лукьянов, С.С. Круглов
ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ Руководство к практическим занятиям В лаборатории процессов и аппаратов Нефтегазопереработки
Москва 2012 Министерство образования и науки Российской Федерации РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА ИМЕНИ И.М. Губкина
Д.Н. Жедяевский, В.Д. Косьмин, В.А. Лукьянов, С.С. Круглов
ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ Руководство к практическим занятиям В лаборатории процессов и аппаратов нефтегазопереработки
по дисциплинам: «Процессы и аппараты нефтегазопереработки», «Процессы и аппараты химической технологии», «Процессы и аппараты защиты окружающей среды» Учебно-методическое пособие для студентов специальностей: 130603, 240401,240403,280201 и бакалавров по направлениям: 240100, 150400
Москва 2012
УДК 66.048.375
Д.Н. Жедяевский, В.Д. Косьмин, В.А. Лукьянов, С.С. Круглов Гидромеханические процессы. Руководство к практическим занятиям в лаборатории процессов и аппаратов нефтегазопереработки. - М.: РГУ нефти и газа, 2012, 76 с. Учебно-методическое пособие включает теоретические основы гидромеханических процессов: фильтрации, псевдоожижения, витания и осаждения, а так же очистки газов в циклонах, порядок проведения опытов и обработки результатов, контрольные вопросы. Учебно-методическое пособие пpедназначено для студентов специальностей 130603, 240401, 240403, 280201 и бакалавров по направлениям: 240100, 150400, изучающих курс «Процессы и аппараты нефтегазопереработки», «Процессы и аппараты химической технологии», «Процессы и аппараты защиты окружающей среды». Ил. 32, табл. 8, библ. - 6 назв.
Издание подготовлено на кафедре оборудования нефтегазопереработки.
Рецензенты: Кошелев В.Н. профессор, д.х.н.; Мельников В.Б. профессор, д.т.н.
Ó Д.Н. Жедяевский, В.Д. Косьмин, В.А. Лукьянов, С.С. Круглов Ó Издательский центр РГУ нефти и газа имени И.М. Губкина, 2012
Условные обозначения
n - кинематическая вязкость фильтрующегося потока, м2/с
V – объем слоя; VП – суммарный объем поровых каналов в слое; VЧ – суммарный объем твердых частиц в слое. D - диаметра аппарата d - диаметр твердой частицы e - порозность или доля свободного объёма xi - весовое содержание частиц диаметром di wК - скорость потока среды, отнесенная к сечению поровых каналов, м/с; H - высота слоя, м; dК - эквивалентный диаметр поровых каналов, м; r - плотность cреды, кг/м3; l - коэффициент гидравлического сопротивления wК - скорость потока среды в поровых каналах w - скорость потока среды, рассчитанная на полное сечение слоя (скорость фильтрации) m - динамическая вязкость среды, Па с; Re- число Рейнольдса Re ч - число Рейнольдса, отнесенное к диаметру частицы dрш - диаметр равновеликого по объему (весу) шара, м; j - коэффициент формы, Лабораторная работа № 1 ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ НЕПОДВИЖНОГО СЛОЯ ЗЕРНИСТОГО МАТЕРИАЛА Цели лабораторной работы · получение экспериментальной зависимости гидравлического сопротивления слоя зернистого материала от скорости воздуха и размера частиц; · сопоставление экспериментальных значений гидравлического сопротивления слоя зернистого материала с расчетными.
Теоретические основы Среда (жидкость или газ) движется через неподвижный слой зернистого материала, проходя в свободном объеме по каналам между твердыми частицами. Движение потока среды через слой сыпучего материала характеризуется периодическими сужениями и расширениями отдельных струй, на которые разделяется поток среды при входе в слой, и извилистостью пути струй по поровым каналам. Характер движения потока в слое, частота сужений и расширений отдельных струй, а также их извилистость определяются размером и шероховатостью частиц слоя зернистого материала, их фракционным составом, формой и упорядоченностью укладки, величиной объема пустот между частицами, влиянием стенок аппарата, определяемым отношением диаметра аппарата D к диаметру частицы слоя d, величиной внешней поверхности слоя в единице его объема, физическими параметрами потока (плотность, вязкость). Важнейшей характеристикой слоя является его порозность или доля свободного объёма e:
где: V – объем слоя; VП – суммарный объем поровых каналов в слое; VЧ – суммарный объем твердых частиц в слое.
Если слой состоит из частиц одинакового размера, его называют монодисперсным. Зернистые материалы, в том числе катализаторы, применяемые в промышленности, состоят из частиц неодинакового размера. Слой из частиц разного размера называют полидисперсным. Размер частиц может быть определен различными способами. Для крупных частиц (более 5 мм) возможно прямое измерение штангенциркулем или микрометром. Для очень мелких частиц микроскопического порядка (менее 0,04 мм) используются косвенные методы, основанные на измерении скорости осаждения. Гранулометрический состав частицы промежуточного размера определяют просеиванием. Для этой цели используются сита с различным размером перфорации. При проведении гидродинамических расчетов пользуются величиной среднего диаметра частиц. Так, для слоя, состоящего из шаров различных размеров с весовым содержанием xi частиц диаметром di, их средний диаметр определяется как средневзвешенную величину:
Скоростью фильтрации, или фиктивной скоростью, называют среднюю скорость потока, отнесенную к поперечному сечению аппарата. Гидравлическое сопротивление слоя зернистого материала (потеря напора в слое) может быть определено по уравнению Дарси-Вейсбаха:
где: wК - скорость потока в сечении поровых каналов; H - высота слоя; dК - эквивалентный диаметр поровых каналов; r - плотность cреды; l - коэффициент гидравлического сопротивления. Скорость потока среды в поровых каналах wК можно определить через скорость потока среды, рассчитанную на полное сечение слоя w (скорость фильтрации):
Для монодисперсного слоя, состоящего из шарообразных частиц диаметром d, эквивалентный диаметр порового канала равен
С учетом этой зависимости, уравнение (1.3) для расчета гидравлического сопротивления при движении потока в слое зернистого материала можно представить следующим образом
Коэффициент гидравлического сопротивления l может быть определен по уравнению:
где: A и B - коэффициенты, зависящие от условий взаимодействия потока и слоя твердых частиц; Re - число Рейнольдса. Число Рейнольдса Re определяется уравнением:
Заменив в уравнении (1.8) скорость потока в каналах и размер сечения канала на выражения, полученные ранее, получим
где: m - динамическая вязкость среды, Па с; Re ч - число Рейнольдса, отнесенное к диаметру частицы:
Значения плотности и вязкости среды соответствуют средней температуре потока в слое. Если подставить в уравнение (1.6) значение коэффициента гидравлического сопротивления из выражения (1.7), с учетом того, что A = 134 и B = 2,34, то получаем расчетное уравнение, предложенное Эргуном, которое хорошо описывает экспериментальные данные различных авторов по гидравлическому сопротивлению слоя зернистого материала и рекомендуется для технических расчетов:
Для слоя зернистого материала при свободной укладке расчетные значения, полученные по уравнению (1.11) совпадают с экспериментальными данными с точностью ±25%. Это уравнение не рекомендуется применять для плотных слоев с упорядоченной укладкой или засыпок с повышенной порозностью (e = 0,6÷0,98). При высоких значениях порозности перепад давления, полученный расчетным путем из уравнения Эргуна может быть значительно меньше экспериментальных данных.
Согласно уравнению (1.11) падение давления представляет собой сумму двух составляющих: потеря напора на трение за счет сил вязкости (вязкостные потери) и потеря напора, обусловленная потерей кинетической энергии потока при его движении по каналам между частицами слоя. При малых значениях критерия Рейнольдса потеря напора, обусловленная потерей кинетической энергии потока, относительно мала и ею можно пренебреч. Исходя из этого уравнение (1.11) примет вид:
При больших значениях критерия Рейнольдса, наоборот, из-за относительно малой величины потери напора на трение можно учитывать только потерю напора, обусловленная потерей кинетической энергии потока. Тогда уравнение (1.11) примет вид:
Наряду с уравнением Эргуна в практике расчетов потерь напора в неподвижном слое зернистого материала используются эмпирические зависимости, приведенные в табл.1.1. Таблица 1.1
Частицы не шарообразной формы характеризуются эквивалентным диаметром:
где: dрш - диаметр равновеликого по объему (весу) шара, м; j - коэффициент формы, равный отношению поверхности равновеликого по объему шара к поверхности частицы. Некоторые значения коэффициентов формы частиц приведены в таблицах П-3 и П-4 приложений.
Рис. 1.1. Схема лабораторной установки для изучения гидравлического сопротивления слоя зернистого материала
Установка состоит из трех цилиндров 8 с внутренним диаметром d = 40 мм. Цилиндры частично заполнены зернистыми материалами с различными характеристиками. Характеристики зернистых материалов приведены в таблице П-1 приложений. Высота слоя зернистого материала во всех цилиндрах одинакова и составляет H = 0,15 м. Воздух в установку подается через кран 1. Регулирующий вентиль 2 служит для возможной регулировки расхода воздуха путем частичного сброса воздуха в атмосферу. Воздух попадает в верхнюю часть цилиндров над слоем зернистого материала, проходит через слой зернистого материала и через перфорированные пластины 9 сбрасывается в атмосферу. Расход воздуха измеряется ротаметром 3, температура воздуха – термометром 4. Переключение подачи воздуха между цилиндрами производится с помощью кранов 5. Избыточное давление внутри цилиндров над слоем зернистого материала измеряется манометром 6. Подключение манометра к находящемуся в работе цилиндру производится кранами 7.
Обработка результатов
Обработка результатов измерений включает расчет величины гидравлического сопротивления слоя частиц по формуле Эргуна (1.11) и сопоставление рассчетных величин с экспериментальными данными. Обработку данных для каждой серии проводят в следующей последовательности: 1. Рассчитывают экспериментальное значение гидравлического сопротивления слоя зернистого материала (DP/H) эксп. Перепад давления DP’ на слое зернистого материала в нашем случае будет равен показанию манометра 6. Результаты заносят в таблицу 1.2. 2. По тарировочной зависимости (рис. П-1 приложений) определяют расход воздуха Q, подаваемого в установку в зависимости от показаний ротаметра. Результаты заносят в таблицу 1.2. 2. Рассчитывают абсолютное давление воздуха в цилиндре над слоем зернистого материала:
3. Рассчитывают абсолютное давление воздуха в середине слоя зернистого материала:
4. Определяют площадь свободного сечения цилиндра:
5. Определяют скорость воздуха в свободном сечении цилиндра при среднем давлении в слое:
где F - площадь свободного сечения цилиндра. 6. Пользуясь характеристиками зернистого материала из таблицы П-1 приложений определяют порозность e слоя:
где rн - кажущаяся (насыпная) плотность слоя зернистого материала (плотность, рассчитываемая как отношение массы вещества к занимаемому им объёму); rч - плотность материала частиц слоя зернистого материала; 7. По таблице П-2 приложений в зависимости от температуры t определяют вязкость воздуха m. 8. Определяют плотность воздуха по формуле:
9. Определяют гидравлическое сопротивление слоя зернистого материала по формуле Эргуна (1.11) DP/H. Результаты заносят в таблицу 1.2. 10. Определяют относительное отклонение экспериментального значения гидравлического сопротивления слоя зернистого материала от расчетного значения:
Результаты заносят в таблицу 1.2. Указанные расчеты проводят для каждого опыта. 11. Экспериментальные и расчетные данные для каждого вида исследованного материала представляют в виде графиков зависимостей ΔР/Н = f (w). Вопросы для самоконтроля 1. Кажущаяся (насыпная) плотность зернистого материала. 2. Эквивалентный диаметр порового канала. 3. Порозность слоя. Определение порозности. 4. Уравнение для расчета величины критерия Рейнольдса при движении потока в слое зернистого материала. 5. Скорость фильтрации. 6. Фактическая средняя скорость потока в поровых каналах. 7. Определение расхода воздуха в работе. 8. Расчет абсолютного давления воздуха в слое. 9. Уравнения Дарси-Вейсбаха и Эргуна. 10. Коэффициент формы частиц зернистого материала. 11. Определение потери напора при движении потока в слое зернистого материала. Лабораторная работа № 2 ЗЕРНИСТОГО МАТЕРИАЛА Цели лабораторной работы · экспериментальное и теоретическое определение скорости начала псевдоожижения слоя зернистого материала; · сопоставление экспериментальных значений скорости начала псевдоожижения слоя зернистого материала с расчетными; · определение кажущейся (насыпной) плотности и порозности кипящего и неподвижного слоя зернистого материала.
Теоретические основы В нефтеперерабатывающей и нефтехимической промышленности многие технологические процессы используют в производственных масштабах технику псевдоожижения. Большое распространение получил процесс каталитического крекинга дистиллятного иостаточного сырья в кипящем (псевдоожиженном) слое катализатора, являющийся одним из основных вторичных процессов переработки углеводородного сырья, позволяющим получать высокооктановые авиационные и автомобильные бензины. Слой зернистого материала представляет собой объем, заполненый мелкими частицами материала, пустоты между которыми образуют извилистые поровые каналы, по которым движется поток газа. Частицы зернистого материала могут иметь различные размеры и форму (сферы, цилиндры, таблетки, зерна произвольной формы и т.д.). Для характеристики формы частиц используют коэффициент формы
где Fш – площадь поверхности шара, объём которого равен объёму частицы; Fч - площадь поверхности частицы. В общем случае Коэффициент формы Для частиц неправильной формы коэффициент Важнейшей характеристикой слоя зернистого материала является его порозность ε или доля объёма пустот между частицами от общего объема слоя (доля свободного объема):
где V - объем слоя; Vч - объем, занимаемый частицами; Vп - объем, занимаемый поровыми каналами. Порозность можно выразить через кажущуюся (насыпную) и истинную плотности слоя зернистого материала:
где rн – кажущаяся (насыпная) плотность слоя; rч - истинная плотность слоя, плотность материала частиц. Слой может быть монодисперсным, т.е. состоять из частиц одинакового размера, или полидисперсным, т.е. состоять из частиц разного размера. При восходящем движении среды (газа, жидкости) через неподвижный слой зернистого материала в сосуде, имеющем свободное пространство над слоем, по мере увеличения скорости потока увеличивается гидравлическое сопротивление слоя и ослабевает давление частиц друг на друга. При достижении некоторого критического значения скорости потока При дальнейшем увеличении скорости газа w > wкp слой переходит во взвешенное состояние. Взвешенный слой зернистого, порошкообразного материала по внешнему виду похож на кипящую жидкость, поэтому его часто называют «кипящим» или псевдоожиженным слоем. Структура слоя в зависимости от скорости восходящего (псевдоожижающего) потока, размера и формы частиц может быть различной. При невысоких скоростях потока, одинаковых размерах и форме твердых частиц может быть получен взвешенный слой с равномерным распределением твердой фазы независимо от продолжительности процесса и размеров аппарата. Такой слой называют однородным. Однородное псевдоожижение для значительного диапазона скоростей наблюдаётся при псевдоожижении зернистых материалов капельными жидкостями. При псевдоожижении по мере роста скорости потока газа в слое образуются пузыри, а на поверхности слоя возникают всплески. При этом наблюдаются значительные пульсации статического и динамического напора псевдоожижающего агента. Такой характер гидродинамики слоя называют неоднородным псевдоожижением. Частицы в таком слое хаотически перемещаются внутри его, что способствует интенсивному тепло и массообмену внутри слоя. Характер движения образующихся пузырей и интенсивность их проскока через слой зависят от скорости газа, гранулометрического состава частиц, отношения высоты слоя к диаметру аппарата, конструкции распределительной решетки, свойств среды и др. Итак, при плавном увеличении скорости потока через слой зернистого материала до некоторого критического значения На рис. 2.1 представлен график зависимости перепада статического давления в слое зернистого материала от скорости среды
Рис. 2.1. Идеальная кривая псевдоожижения Приведенная форма кривой псевдоожижения является идеальной и характерна лишь для гладких, сухих, шаров одинакового размера. Процессу фильтрации соответствует восходящий участок 1, отрезок ОА. При ламинарном режиме фильтрации потока через слой участок 1 представляет собой прямую линию (ΔР ~ w), при турбулентном - параболу (ΔР ~ w2). При достижении скоростью среды критического значения wкр в точке А слой переходит в псевдоожиженное состояние. Участок 2 соответствует псевдоожиженному состоянию слоя. В точке В скорость среды становиться равной скорости витания. На участке 3 при скорости среды превышающей скорость витания частиц, происходит процесс уноса частиц зернистого материала из слоя и гидравлическое сопротивление вследствие этого падает. Вид реальных кривых псевдоожижения показан на рис. 2.2 и рис. 2.3.
Рис. 2.2. Реальная кривая псевдоожижения с гистерезисом
Рис. 2.3. Реальная кривая псевдоожижения Для полидисперсной системы
Для кривой, изображенной на рис. 2, характерно наличие пика ΔР* и гистерезиса, которые обусловлены силами сцепления между частицами слоя и трением частиц о стенки аппарата. Для аппаратов постоянного сечения величина ΔР обычно не превышает 1,5% - 5% от перепада давления ΔР в слое в состоянии псевдоожижения. В аппаратах с увеличивающейся площадью поперечного сечения величина ΔР* может в 2-3 раза превышать величину ΔР. В таких аппаратах образуется так называемый фонтанирующий слой. Для полидисперсных систем характерна «размытость» момента начала псевдоожижения (см. рис. 2.3). Это объясняется тем, что для разных фракций частиц псевдоожижение начинается при разных критических скоростях и на процесс взаимодействия крупных частиц с потоком оказывают влияние уже «ожиженные» мелкие фракции. Для определения скорости начала псевдоожижения слоя в этом случае используют понятие эквивалентного диаметра частиц. Использование эффекта псевдоожижения зернистых материалов позволяет перемещать твердые сыпучие материалы подобно жидкости и, благодаря этому, осуществлять многие процессы непрерывным методом. Интенсивное перемешивание фаз в условиях взвешенного слоя обуславливает высокую эффективность протекающих процессов, при этом значительно возрастает скорость внешней диффузии и теплообмена между потоком и частицами, легко обеспечивается выравнивание температур в большом объеме слоя и др. Для расчета аппаратов с псевдоожиженным слоем необходимо знать величину критической скорости псевдоожижения wKp. В режиме псевдоожижения вес слоя зернистого материала с учетом силы Архимеда действующей на частицы уравновешивается силой гидравлического сопротивления слоя. В этом случае баланс сил для сечения псевдоожиженного слоя, находящегося на расстоянии Н от его поверхности, записывается в следующем виде:
где: rч, r - плотности материала частиц слоя и среды соответственно; ε - порозность неподвижного слоя; F - площадь поперечного сечения слоя. Потеря напора на единицу высоты слоя в широком диапазоне скоростей может быть описана универсальным, справедливым для ламинарного, переходного и турбулентного режимов, уравнением Эргуна:
где: µ - динамическая вязкость среды; d - диаметр частиц слоя. С учетом уравнений (2.4) и (2.5) определим критерий Рейнольдся для начала режима псевдоожижения, т.е. при минимальной скорости потока, при которой слой переходит во взвешенное состояние:
где Ar – критерий Архимеда:
Решая совместно уравнения (2.6) и (2.7) можно определить скорость начала псевдоожижения wкp. Следует учитывать, что в полидисперсном слое, т.е. в слое, сосотоящем из фракций частиц различных размеров, величина wкp для самых крупных частиц может оказаться больше, чем величина wв для самых мелких частиц. В этом случае унос мелких частиц из слоя может наступить раньше, чем крупные частицы перейдут во взвешенное состояние. Различие в размерах частиц, входящих в состав полидисперсного слоя, оказывает влияние на порозность слоя, режим псевдоожижения, однородность слоя, а, следовательно, и на эффективность процессов, протекающих в псевдоожиженном слое. Высота псевдоожиженного слоя Н связана с высотой неподвижного слоя Но соотношением:
где: Н и Но- высоты псевдоожиженного и неподвижного слоев соответственно; e и e0 - порозности псевдоожиженного и неподвижного слоев соответственно.
Рис. 2.4. Схема лабораторной установки Обработка результатов Обработка результатов измерений включает расчет величины скорости начала псевдоожижения и сопоставление расчетных величин с экспериментальными данными. Обработку данных для каждой серии проводят в следующей последовательности: 1. По тарировочной зависимости реометра, приведенной на рис. П-2 приложений, определяют расход воздуха Q, подаваемого в цилиндр в зависимости от показаний реометра. Результаты заносят в таблицу 2.1. 2. Определяют скорость потока воздуха в свободной сечении цилиндра по формуле:
где F - площадь свободного сечения цилиндра. Таблица 2.1 Вопросы для самоконтроля 1. Определение «кипящего» слоя зернистого материала. 2. Порядок экспериментального определения скорости начала псевдоожижения слоя зернистого материала. 3. Алгоритм определения скорости начала псевдоожижения по формулам, рассматриваемым в теоретической части лабораторной работы. 4. Параметры, влияющие на величину скорости начала псевдоожижения слоя зернистого материала. 5. Режимы фильтрации потока газа через неподвижный слой зернистого материала. 6. Влияние скорости потока среды на порозность и плотность псевдоожиженного слоя. 7. Преимущества и недостатки «кипящего» слоя по сравнению с неподвижным слоем зернистого материала. Лабораторная работа № 3 Цели лабораторной работы · экспериментальное определение скоростей витания частиц различной формы в потоке воздуха; · сравнение экспериментальных данных с расчетными.
Теоретические основы Скоростью витания называется скорость потока среды, при которой частицы слоя зернистого материала переходят во взвешенное состояние, т.е. величина подъемной силы потока, действующей на отдельную частицу, уравновешивает её вес. Скорость витания служит верхним пределом существования псевдоожиженного слоя зернистого материала данного гранулометрического состава. Если скорость потока превышает скорость витания, частицы зернистого материала, начиная с наиболее мелких, начинают выноситься из слоя, изменяя тем самым гранулометрический состав материала. Для расчета скоростей витания частиц наибольшее распространение получило критериальное уравнение Тоддеса О.М., Горошко В,Д. и Розенбаума Р.Б., справедливое для всех режимов обтекания частицы потоком: ламинарного, переходного и турбулентного:
где Re и Ar - критерии Рейнольдса и Архимеда соответственно; e - доля свободного сечения в месте нахождения частицы от общего свободного сечения или порозность слоя. Критерий Архимеда Ar рассчитывается по уравнению:
где g - ускорение силы тяжести; d – диаметр частицы; rч - плотность материала частицы; r - плотность потока; m - динамическая вязкость потока. Для турбулентного режима обтекания частицы потоком значения критерия Архимеда сравнительно высоки. Учитывая это, первым слагаемым знаменателя уравнения (3.) можно пренебречь:
или
С другой стороны мы можем определить критерий Рейнольдса как:
где Wв - скорость витания частицы. Решая совместно уравнения (3.4) и (3.5), получим выражение для определения скорости витания частиц сферической формы при турбулентном режиме обтекания потоком:
Рассматривая процесс витания частиц несферической формы для их характеристики пользуются понятием эквивалентного диаметра. Под эквивалентным диаметром подразумевают диаметр сферической частицы из материала той же плотности, которая в восходящем потоке среды имеет ту же скорость витания, что и частица несферической формы. Из уравнения (3.6) можно получить выражение для расчета эквивалентного диаметра частиц несферической формы, предварительно экспериментально определив их скорость витания:
Скорость витания так же можно найти из условия равновесия сил действующих на частицу во взвешенном состоянии. Рассмотрим одиночную частицу зернистого материала находящуюся в восходящем потоке среды (рис. 3.1). Подъемная сила потока R, действующая на частицу, определяется скоростью потока W0 в сечении каналов, не занятых частицами. Подъемная сила равна произведению перепада давления потока ΔP на площадь проекции S0 частицы на плоскость, перпендикулярную направлению движения потока.
где: ξ - коэффициент гидравлического сопротивления при обтекании частицы потоком; ρ - плотность потока; W0 - скорость потока среды в сечении, не занятом частицами.
Рис. 3.1. Частица в восходящем потоке среды Для частиц, площадь проекции S0 которых мала по сравнению с сечением каналов не занятых частицами, скорость W0 можно считать равной скорости потока в свободном сечении W, т.е. W ≈ W0 . В момент перехода частицы слоя во взвешенное состояние подъёмная сила потока R становиться равной разности силы тяжести G и выталкивающей силы потока G’, действующих на частицу.
где g - ускорение силы тяжести; Vч – обем частицы; rч – плотность материала частицы; r – плотность среды. Объединив уравнения (3.8) и (3.9), получим:
Для частицы сферической формы диаметром d уравнение (3.10) примет вид:
Выразим скорость витания:
В данной лабораторной работе режим обтекания частиц потоком среды является турбулентным. Для турбулентного режима коэффициент гидравлического сопротивления ξ можно определить из уравнения Петиджена и Христиансена:
где j - коэффициент формы (или фактор формы) частицы. Коэффициент формы j (или фактор формы) частицы определяется как:
где Fрш – площадь поверхности равновеликого шара, т.е. шара, объём которого равен объёму частицы; Fч - площадь поверхности частицы. Коэффициент формы j частиц геометрически правильной формы определяется аналитически. Для наиболее часто встречающихся форм частиц рассчитанные коэффициенты формы приведены в таблице П-3 приложений. Для частиц неправильной формы коэффициент j находят экспериментально. Для некоторых сыпучих материалов и насадок коэффициенты формы приведены в таблице П-4 приложений. В общем случае значение коэффициента формы лежит в пределах Подставляя j = 1 в уранвнение (3.12) для сферических частиц при турбулентном режиме обтекания получим коэффициент гидравлического сопротивления ξ = 0,44. Подставив величину ξ = 0,44 в уравнение (3.12) получим выражение для скорости витания сферических частиц при турбулентном режиме обтекания:
Для определения скорости витания частиц несферической формы в расчетах вместо диаметра частицы d используют диаметр равновеликого шара dрш, шара, объем Vрш которого равен объему частицы Vч:
Рис. 3.2. Схема лабораторной установки Обработка результатов Обработка результатов измерений включает расчет величин скоростей витания для частиц кубической и сферической форм и сопоставление расчетных величин с экспериментальными данными. Обработку данных проводят в следующей последовательности: 1. По тарировочному графику для диафрагмы, приведенной на рис. П-3 приложений, определяют расход воздуха Q’ через диафрагму в зависимости от перепада давления на диафрагме DP:
где P1 и P2 – избыточные давления воздуха до и после диафрагмы соответственно. 2. Определяют расход воздуха в цилиндре с учетом поправки на изменение давления:
В этом случае давление воздуха в цилиндре принимается равным барометрическому давлению в лаборатории. 3. Рассчитывают скорость витания частицы:
где F - площадь свободного сечения цилиндра. Расчеты проводят для частиц кубической и сферической форм, результаты заносят в таблицу 3.1. 4. Для сферической частицы по уравнению
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.0.57 (0.018 с.) |

 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4)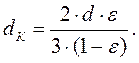 (1.5)
(1.5) (1.6)
(1.6)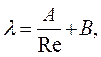 (1.7)
(1.7) (1.8)
(1.8) (1.9)
(1.9) (1.10)
(1.10) (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13)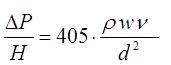








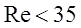


 (1.14)
(1.14) (1.15)
(1.15) (1.16)
(1.16) (1.17)
(1.17) (1.18)
(1.18) (1.19)
(1.19) (1.20)
(1.20) (1.21)
(1.21) (или фактор формы):
(или фактор формы): (2.1)
(2.1) ; для сферических частиц
; для сферических частиц  .
. (2.2)
(2.2) (2.3)
(2.3) силы трения среды о поверхность частиц и инерционные силы потока уравновешивают силы тяжести слоя частиц, то есть сила сопротивления слоя становится равной силе тяжести слоя. В этот момент частицы слоя перестают оказывать давление друг на друга, они становятся подвижными.
силы трения среды о поверхность частиц и инерционные силы потока уравновешивают силы тяжести слоя частиц, то есть сила сопротивления слоя становится равной силе тяжести слоя. В этот момент частицы слоя перестают оказывать давление друг на друга, они становятся подвижными. , называемый кривой псевдоожижения.
, называемый кривой псевдоожижения.


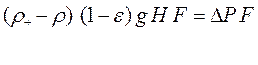 (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8)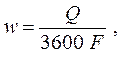 (2.9)
(2.9) (3.1)
(3.1) (3.2)
(3.2) (3.3)
(3.3) . (3.4)
. (3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) , (3.8)
, (3.8)
 (3.9)
(3.9) (3.10)
(3.10) (3.11)
(3.11) (3.12)
(3.12) (3.12)
(3.12) (3.13)
(3.13) ; для сферических частиц j = 1.
; для сферических частиц j = 1. (3.14)
(3.14) (3.15)
(3.15) (3.16)
(3.16) (3.17)
(3.17) (3.18)
(3.18)


