
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача из выполнения экспериментального исследованияСодержание книги Поиск на нашем сайте
3.1 Собрать принципиальную электрическую схему цепи. 3.2 Подать напряжение на зажимы экспериментальной установки. 3.3 Снять показания приборов, предварительно установив рассчитанную величину емкости конденсатора для полной компенсации реактивной мощности катушки, результаты занести в таблицу 3. Таблица 3
3.4 Определить с помощью экспериментальных данных действующее значение напряжения на зажимах электрической цепи.
3.5 Определить с помощью экспериментальных данных действующее значение напряжения на зажимах катушки и конденсатора. 3.6 Определить с помощью экспериментальных данных действующее значение силы тока в линии электропередачи.
3.7 Определить с помощью экспериментальных данных действующее значение силы тока в катушке.
3.8 Определить с помощью экспериментальных данных действующее значение силы тока в конденсаторе.
3.9 Определить с помощью экспериментальных данных активную мощность, потребляемую электрической цепью.
3.10 Определить с помощью экспериментальных данных полную мощность электрической цепи, используя уравнение: S = U·I.
3.11 Определить с помощью экспериментальных и расчетных данных коэффициент мощности электрической цепи, используя уравнение: cos φ =
3.12 Определить с помощью экспериментальных и расчетных данных угол сдвига фаз электрической цепи, используя уравнение: φ = arccos
3.13 Определить с помощью экспериментальных данных действующее значение реактивной составляющей силы тока в катушке, используя уравнение: Iр = bL· U 2.
3.14 Определить с помощью экспериментальных данных действующее значение активной составной силы тока в катушке, используя уравнение: I1 =
3.15 Определить с помощью экспериментальных данных действующее значение реактивной составляющей силы тока в конденсаторе.
3.16 Определить с помощью экспериментальных и расчетных данных реактивную мощность электрической цепи, используя уравнение: Q = (bL – bC) U 22.
3.17 Построить в выбранном масштабе векторную диаграмму действующих значений сил токов и напряжений в электрической цепи, приняв, что начальная фаза напряжения на катушке равняется нулю.
3.18 Результаты расчетов занести в таблицы 4 и 5.
Таблица 4
Таблица 5
Тематическое комплексное квалификационное задание
Условие От источника переменного синусоидального напряжения по линии электропередачи запитана активно-индуктивная нагрузка, в качестве которой используется реальная катушка индуктивности. В цепи установлены следующие электроизмерительные приборы: в начале линии электропередачи – амперметр, вольтметр и ваттметр; в конце линии электропередачи – вольтметр. Для компенсации реактивной мощности параллельно нагрузке через выключатель S включён идеальный конденсатор С. Напряжение в начале линии электропередачи u 1. Параметры линии электропередачи: активное сопротивление r л, индуктивное сопротивление х л. Параметры нагрузки: активное сопротивление катушки r 2, индуктивное сопротивление катушки х 2. Задан коэффициент мощности нагрузки cos φз. Задано номинальное напряжение нагрузки U 2 н . Задание 1. Составить принципиальную электрическую схему описанной электрической цепи. Отдельные элементы цепи выделить жирными линиями, а их соединяющие провода – тонкими линиями. 2. Описать физические явления, наблюдаемые в линии электропередачи. Описать физические явления, наблюдаемые в нагрузке. 3. Составить расчётную схему электрической цепи при выключенном выключателе S в комплексной форме, приняв следующие допущения: – сопротивления прямого и обратного проводов линии электропередачи сосредоточить в одном месте; – сопротивлениями проводов, соединяющих элементы цепи, пренебречь; – сопротивлениями амперметра и токовой обмоткой ваттметра пренебречь; – сопротивления вольтметра и обмотки напряжения ваттметра считать равными бесконечности. Выполнить следующие обозначения: – обозначить зажимы в начале линии электропередачи цифрами 1 и 2, а зажимы в конце линии электропередачи цифрами 3 и 4; – обозначить комплекс силы тока в линии электропередачи 4. Выполнить расчёт электрической цепи рассмотренной в пункте 3: 4.1) записать комплекс полного сопротивления линии электропередачи Z л в алгебраической форме; 4.2) рассчитать комплекс полного сопротивления линии электропередачи Z л в показательной форме; 4.3) записать комплекс полного сопротивления нагрузки Z 2 в алгебраической форме; 4.4) рассчитать комплекс полного сопротивления нагрузки Z 2 в показательной форме; 4.5) записать комплекс действующего значения напряжения на зажимах данной цепи 4.6) рассчитать комплекс эквивалентного полного сопротивления всей цепи ZЭ в алгебраической форме; 4.7) записать комплекс эквивалентного полного сопротивления всей цепи ZЭ в показательной форме; 4.8) рассчитать комплекс действующего значения силы электрического тока в линии электропередачи 4.9) рассчитать комплекс действующего значения падения напряжения на активном сопротивлении линии электропередачи 4.10) рассчитать комплекс действующего значения падения напряжения на индуктивном сопротивлении линии электропередачи 4.11) рассчитать комплекс действующего значения падения напряжения в линии электропередачи 4.12) рассчитать комплекс действующего значения падения напряжения на активном сопротивлении нагрузки 4.13) рассчитать комплекс действующего значения падения напряжения на индуктивном сопротивлении нагрузки 4.14) рассчитать комплекс действующего значения напряжения на зажимах нагрузки 4.15) рассчитать действующее значение падения напряжения в линии электропередачи U л; 4.16) рассчитать потери напряжения в линии электропередачи 4.17) рассчитать потери активной мощности в линии электропередачи 4.18) построить на комплексной плоскости в масштабе векторную диаграмму действующих значений напряжений и тока для всей цепи. 5. Построить круговую диаграмму – комплекс действующего значения силы тока короткого замыкания – угол ψ. 6. Найти из круговой диаграммы комплекс действующей силы тока 7. Составить расчётную схему электрической цепи при включенном выключателе S в комплексной форме, приняв допущения изложенные в п. 3. 8. Выполнить расчёт электрической цепи рассмотренной в пункте 7: 8.1) рассчитать активную мощность Р 2, потребляемую нагрузкой при заданном номинальном напряжении на её зажимах; 8.2) рассчитать реактивную ёмкостную мощность конденсатора Q C при номинальном напряжении на зажимах нагрузки и заданном коэффициенте мощности cos φз; 8.3) рассчитать действующее значение силы тока в конденсаторе 8.4) рассчитать реактивное ёмкостное сопротивление конденсатора хС; 8.5) рассчитать комплекс полного сопротивления участка цепи между узлами 3 и 4 Z34 в показательной форме; 8.6) рассчитать комплекс полного сопротивления эквивалентного участка цепи Z34 в алгебраической форме; 8.7) рассчитать комплекс эквивалентного полного сопротивления всей цепи Z Э в алгебраической форме; 8.8) записать комплекс эквивалентного полного сопротивления всей цепи Z Э в показательной форме; 8.9) рассчитать комплекс действующего значения силы электрического тока в линии электропередачи 8.10) рассчитать комплекс действующего значения падения напряжения на активном сопротивлении линии электропередачи после компенсации 8.11) рассчитать комплекс действующего значения падения напряжения на индуктивном сопротивлении линии электропередачи после компенсации 8.12) рассчитать комплекс действующего значения падения напряжения в линии электропередачи после компенсации 8.13) рассчитать комплекс действующего значения падения напряжения на активном сопротивлении участка цепи между узлами 3 и 4 8.14) рассчитать комплекс действующего значения падения напряжения на индуктивном сопротивлении участка цепи между узлами 3 и 4 8.15) рассчитать комплекс действующего значения падениям на зажимах нагрузки 3 и 4 8.16) рассчитать действующее значение падения напряжения в линии электропередачи после компенсации 8.17) рассчитать потери напряжения в линии электропередачи после компенсации 8.18) рассчитать потери активной мощности в линии электропередачи после компенсации 9. Сделать вывод. Варианты исходных данных к тематическому комплексному Квалификационному заданию
Таблица 6.10
Пример оформления
Рисунок 1 – …
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.142 (0.009 с.) |

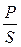 .
.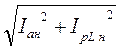 .
.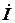 , комплекс падения напряжения в линии электропередачи
, комплекс падения напряжения в линии электропередачи 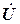 л, комплекс напряжения на зажимах нагрузки
л, комплекс напряжения на зажимах нагрузки  .
. в показательной форме;
в показательной форме; в показательной форме;
в показательной форме;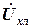 в показательной форме;
в показательной форме; л;
л;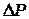 л;
л;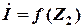 при cos φ 2 = const, для чего определите:
при cos φ 2 = const, для чего определите: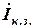 ;
;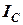 при заданном номинальном напряжении на зажимах нагрузки;
при заданном номинальном напряжении на зажимах нагрузки;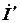 после компенсации в показательной форме;
после компенсации в показательной форме;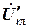 в показательной форме;
в показательной форме; в показательной форме;
в показательной форме;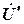 л в показательной форме;
л в показательной форме;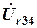 в показательной форме;
в показательной форме;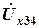 в показательной форме;
в показательной форме; в показательной форме;
в показательной форме;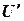 л;
л;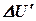 л;
л; л.
л.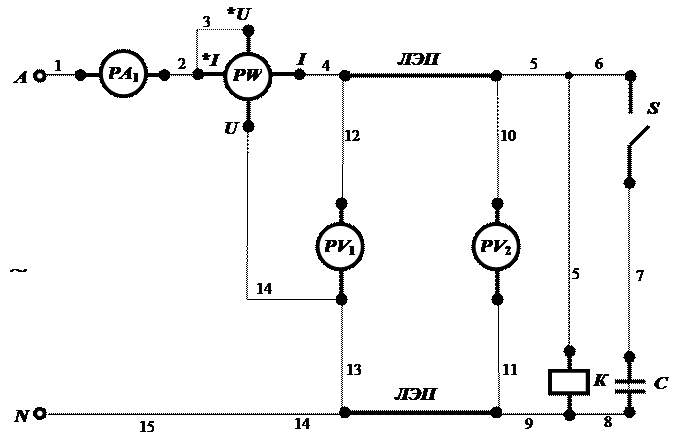 1. Составляем принципиальную электрическую схему описанной электрической цепи:
1. Составляем принципиальную электрическую схему описанной электрической цепи:


