
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лимитная схема декомпозиции по модели максимизации цфп.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
По такой схеме центр выделяет лимиты централизованных ресурсов (ЦР) каждой подсистеме, а подсистемы в пределах выделенных централизованных и имеющихся собственных ресурсов решают свои задачи на максимум собственных ЦФП. При этом при известных ресурсах каждая подсистема определяет оптимальный номенклатурный вектор продукции. Центр таким образом распределяет централизованные ресурсы между подсистемами, что в результате решения каждой подсистемой своей оптимизационной задачи получается глобальный оптимум для всей системы. Представим модель в векторной форме. Для этого введем обозначения:
- потребность в централизованном ресурсе к -ой подсистемы;
- количество централизованного ресурса;
- потребность в собственном ресурсе к -ой подсис- темы;
Тогда модель в векторной форме будет иметь следующий вид:
В соответствии с принципами лимитной схемы декомпозиции каждой подсистеме выделяется лимит централизованных ресурсов. Обозначим:
- количество централизованного ресурса, выделяемого каждой подсистеме.
Причем необходимо обязательное выполнение условия:
Тогда задача каждой подсистемы будет иметь следующий вид:
Общая модель распадается на модель центра и модели подсистем. Координирующая роль центра состоит в определении оптимальных векторов централизованно распределяемых ресурсов
Подсистемы сообщают эту функцию в центр. Тогда модель центра можно представить таким образом:
А структурная схема общей модели будет иметь вид:
Последовательность расчетов такой декомпозиционной системы следующая: 1. Подсистемы решают свои задачи на максимум собственной ЦФ при различных значениях вектора централизованных ресурсов 2. Центр решает собственную задачу на максимум ГЦФП и определяет оптимальный объем ресурсов 3. В соответствии с выделенным объемом централизованного ресурса
Порядок выполнения контрольных заданий.
Последовательность выполнения работы поясним в ходе решения контрольного примера.
Задание 1. Построение и декомпозиция исходной модели. 1.1. Предположим, что в объединение входят два предприятия, условия функционирования которых представлены в табл. 4 и табл. 5 соответственно. Цены, нормы расходов и объемы ресурсов приведены в условных единицах.
Таблица 4. Данные по первому предприятию
Таблица 5. Данные по второму предприятию
Для каждого предприятия необходимо определить оптимальный объем выпуска продукции в стоимостном выражении, если известно, что объем централизованного ресурса, распределяемого между предприятиями, составляет 32 условные единицы. Обозначим: х 11, х 12 - количество изделий 1-го и 2-го типа 1-ой подсистемы[1]; х 21, х 22 - количество изделий 1-го и 2-го типа 2-ой подсистемы1. Тогда общая модель системы будет иметь следующий вид:
3 х11 + 2 х12 + 2 х21 + 3 х22 2 х11 + 3 х12 + 2 х21 + 1 х22 2 х11 + 1 х12 1 х11 1 х21 + 2 х22 х22 х 11, х 12, х 21, х22
Декомпозиция этой модели приводится на схеме:
Задание 2. Решение задач подсистем.
в центр. Рассмотрим процесс решения задач в каждой подсистеме.
2.1. Решение задачи первой подсистемы. Модель первой подсистемы имеет вид:
3 х11 + 2 х12 2 х11 + 3 х12 2 х11 + 1 х12 1 х11
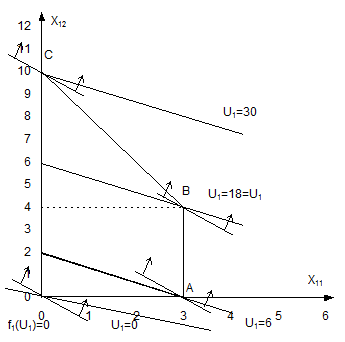
Решение параметрической задачи будем приводить графически. Для этого построим область допустимых решений (ОДР), состоящую из уравнений собственных ресурсов подсистемы, то есть неравенства (2) и (3) (см. рис. 7). На этой области исследуем поведение ЦФ от различных значений ЦР. При значении U1 = 0, f1 (U1) = 0. Начнем увеличивать значение ЦР. Пусть U1 = 6 (область ОАС 1). На этом множестве ЦФ достигает своего оптимального значения в точке А, то есть при увеличении ЦР от 0 до 6 оптимальный план скользит по ребру ОА. А при увеличении U1 от от 6 до 18 оптимальный план скользит по ребру АВ. А при изменении U1 от 18 до 30 оптимальный план скользит по ребру ВС. Таким образом, при изменении ресурса от 0 до 30 оптимальный план первой подсистемы движется по траектории ОАВС. При увеличении U1 сверх 30 данный ресурс уже не является лимитирующим, и оптимальный план остается в точке С. При этом значение ЦФ в точке С f1 (U1) = 20. Для выражения зависимости координат оптимального плана от величины U1 необходимо решить систему уравнений. Первое уравнение является ограничением ЦР, а второе – гранью ОДР, по которой скользит оптимальный план. Последовательно рассмотрим поведение функции на отрезках [ ОА ], [ АВ ], [ ВС ]. 1. Найдем вид функции на отрезке [ ОА ]. На этом отрезке ЦР изменяется от 0 до 6. Система ограничений, из которой находим координаты оптимального плана, имеет следующий вид:
Находим из этой системы координат оптимального плана:
Подставляя эти значения в уравнение ЦФ
2. Отрезок [ АВ ],
3. Отрезок [ ВС ],
4. При Тогда зависимость ЦФ первой подсистемы от ЦР, то есть решение первой подсистемы, будет следующей:
График этой функции представлен на рис.8. Эта зависимость отражает то общее свойство любой производственной системы, что эффективность каждой дополнительной единицы уменьшается, то есть прирост максимально возможного объема выпуска на дополнительную единицу ресурса при неизменной технологии убывает (общий закон убывающей эффективности).
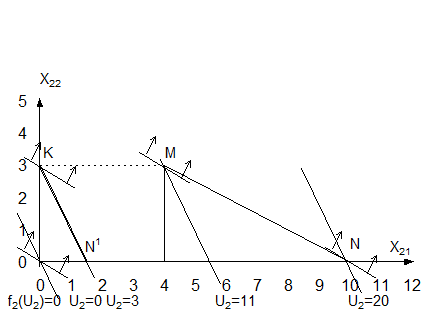
2.2. Решение второй подсистемы. Ее модель: 2 х21 + 3 х22 2 х21 + 1 х22 1 х21 + 2 х22 1 х22 При увеличении ресурса U2 от 0 до 20, оптимальный план, как видно на рис. 9, движется по траектории OKMN. Координаты оптимального плана на различных участках траектории будут следующими:
1. Отрезок [ OK ], 0 ≤ U2 ≤ 3.
2. Отрезок [ KМ ], 3 ≤ U2 ≤ 11.
3. Отрезок [ МN ], 11 ≤ U2 ≤ 20.
4.
Решение второй подсистемы:
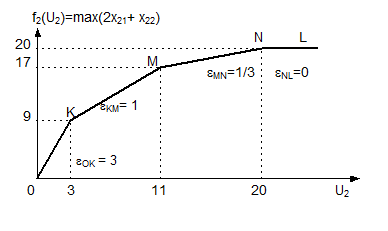
График этой функции представлен на рис. 10. Подсистемы сообщают эти функции в центр.
Задание 3. Решение задачи центра и определение номенклатурных планов подсистем. Задача выглядит следующим образом:
Рис. 7. Решение задачи 1 п/с.
Рис. 8. Линия эффективности 1 п/с.
Рис. 9. Решение задачи 2 п/с.
Рис. 10. Линия эффективности 2 п/с.
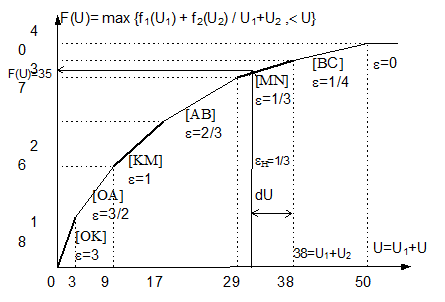
3.1. Для решения этой задачи нужно построить результирующую функцию максимального объема выпуска всей системы в зависимости от объема ЦР. Практически такую функцию можно построить, включая отрезки функций подсистем в порядке убывания эффективности дополнительной единицы ресурса. Для наглядности отрезки первой подсистемы будем изображать тонкой линией, а второй подсистемы – толстой. График результирующей функции представлен на рис. 11. По этой функции определяется предельный норматив эффективности использования ЦР: на оси ресурсов U находится точка, соответствующая наличию ресурса в системе (32). Из этой точки восстанавливается перпендикуляр до пересечения с графиком функции f (U). Соответствующий коэффициент эффективности ε и будет являться предельным (нормативным) для всей системы εН . Для нашего примера:
Этот норматив εН спускается подсистемам, которые не имеют теперь права использовать ЦР с меньшей эффективностью.
3.2. Подсистемы запрашивают такой объем ресурсов UK, эффективность использования которого не меньше, чем предельная. Эти объемы сообщаются в центр. Для нашего примера:
3.3. Центр определяет суммарный объем запрашиваемых ресурсов и их наличие. Если спрос превышает наличие, то заявка подсистемы, имеющей меньшую эффективность использования ресурса, уменьшается на величину сбалансирующего спроса и предложения. Для нашего примера
Значит, на 6 = ∆ U единиц корректируется заявка второй подсистемы. В результате подсистемам спускаются оптимальные нормы централизованного ресурса:
Рис. 11. Построение линии эффективности всей системы и определение eн и
3.4. В соответствии с выделенным объемом ресурсов подсистемы решают собственные задачи при известных ресурсах и определяют оптимальные номенклатурные планы. В данном примере оптимальные планы такие:
Оптимальный объем выпуска продукции в стоимостном выражении: Задание к контрольной работе.
Постановка задачи аналогична приведенному примеру. Нормы расхода ресурсов и цены продукции берутся из таблиц 4 и 5. Объем ресурсов выбирается из таблицы 6 в соответствии с номером варианта. Номер варианта определяется последней цифрой номера зачетной книжки.
Исходные данные по вариантам Таблица 6
Содержание контрольной работы 1. Постановка задачи (исходные данные, п.п 1.1 – 1.2). 2. Графическое решение задач каждой подсистемы (на миллиметровке и в одинаковом масштабе). 3. Решение задачи центра (в том же масштабе). 4. Определение оптимального решения каждой подсистемы. 5. Выводы по работе.
6. Методические указания по изучению дисциплины.
При изучении дисциплины следует обратить внимание на иные способы декомпозиции (2. с. 113-139). Определите, какие проблемы, являющиеся ключевыми в согласовании деятельности центра и подсистем, остались вне рассмотрения. Важнейшей такой проблемой является определение оптимальных нормативов эффективности единовременных затрат (капитальных вложений). При самостоятельной работе особое внимание необходимо обратить на изучение взглядов В.В. Новожилова на данную проблему (1). Попробуйте ответить на вопрос об области применения предложенной схемы декомпозиции.
Список литературы. 1. Новожилов В.В. Проблемы измерения затрат и результатов при оптимальном планировании. М.: Наука, 1972. 2. Оптимизация функционирования социалистической экономики / Под ред. С.С. Шаталина. М.: Изд-во МГУ, 1980. 3. Акулич И.Л. Математическое программирование в примерах и задачах: Учебное пособие для студентов эконом. специальностей. М.: Высшая школа, 1986. 4. Шимко П.Д., Поснов В.Г. Экономко-математическое моделирование производственных систем / ЛИЭИ. Л.:, 1987. 5. Исследование операций: Учеб. пособие для студ. вузов, обуч. по спец. «Прикладная математика» и «Экономическая кибернетика».—М.: Высшая школа,1990.-383 с. 6. Громова Н.В. и др. Методы исследования one— Г 86 раций в моделировании организационно—экономических задач: Учеб. пособие/Громова Н.Б., Минько Э.В., Прохоров В.И.-М.: Изд-во МАИ,1992.-240 с.:ил. 7. Исследование операций в экономике: Учебное пособие для вузов/Под ред. Н.Ш. Кремера.—М.: Банки и биржи, ЮНИТИ,1997.—407 с.:ил., табл. 8. Раковщик Л. С. Исследование операций: Учебное пособие для вузов/СПбГИЭА.-СПб:СПбГИЭА, 1994. 9.-134 с. 9. Паркинсон С. Н., Рустомджи М.К. Искусство управления/ Пер. с англ. К. Савельева.—М.: Издательско—торговый дом Гранд, Агентство Фаир,1997. —271 с.:ил.—(Настольная книга бизнесмена). 10. Семененко А. И. Предпринимательская логистика.— СПб.: Политехника, 1997.— 347 с.
Приложение 1 Пример оформления титульного листа контрольной работы
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный инженерно-экономический университет» (СПбГИЭУ, ИНЖЭКОН)
Кафедра исследования операций в экономике имени профессора Юрия Алексеевича Львова
Контрольная работа по дисциплине
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 503; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.47.194 (0.008 с.) |

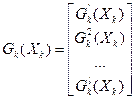
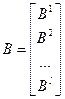
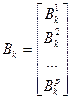 - количество собственного ресурса к -ой подсистемы;
- количество собственного ресурса к -ой подсистемы;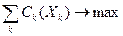
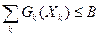
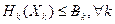 .
.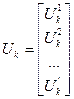
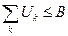
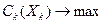

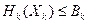
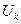 , при которых максимизируется глобальная ЦФ системы. Поскольку максимум ЦФ подсистемы зависит от выделяемых централизованных ресурсов, то в результате решения задачи каждой подсистемы в принципе можно построить следующую функцию:
, при которых максимизируется глобальная ЦФ системы. Поскольку максимум ЦФ подсистемы зависит от выделяемых централизованных ресурсов, то в результате решения задачи каждой подсистемы в принципе можно построить следующую функцию: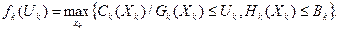
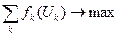
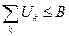 .
.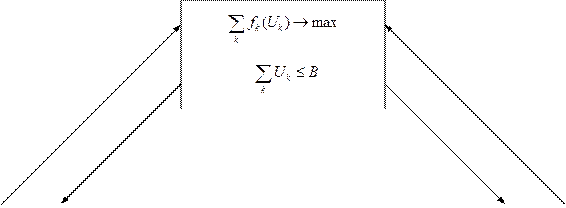



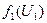
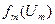
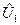
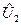
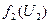
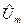

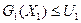
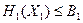
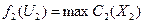
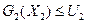

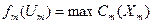
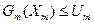
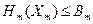
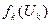 - функцию максимальной полезности деятельности каждой подсистемы в зависимости от наболра ресурсов
- функцию максимальной полезности деятельности каждой подсистемы в зависимости от наболра ресурсов 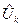 для каждой подсистемы (в пределах имеющегося в центре объема ресурса. Эти объемы спускаются подсистемам.
для каждой подсистемы (в пределах имеющегося в центре объема ресурса. Эти объемы спускаются подсистемам.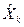 , которые в совокупности соответствуют глобальному оптимальному плану всей системы.
, которые в совокупности соответствуют глобальному оптимальному плану всей системы.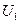
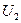
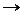 max
max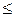 32
32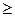 0
0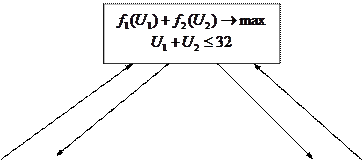
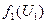

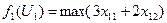
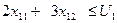
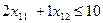

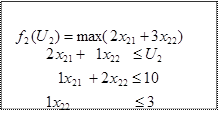
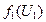
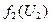 Подсистемы решают собственные параметрические задачи при раз-личных значениях параметров
Подсистемы решают собственные параметрические задачи при раз-личных значениях параметров 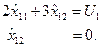
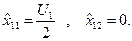
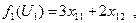 получаем вид функции на отрезке [ ОА ]:
получаем вид функции на отрезке [ ОА ]: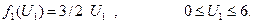
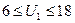 .
.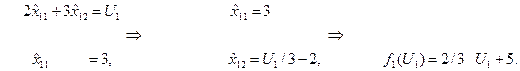
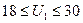 .
.
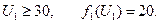
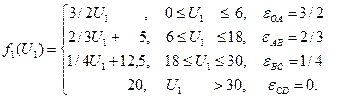
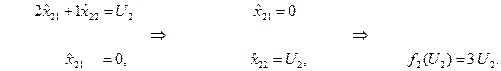
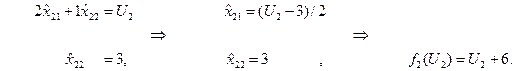
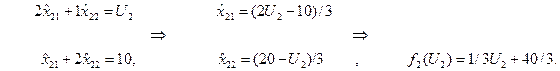
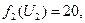 при
при 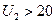 .
.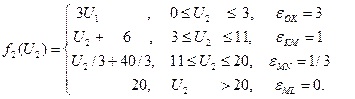

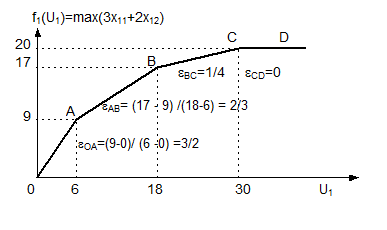
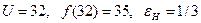 , [ед. ЦФ/ед. ЦР]
, [ед. ЦФ/ед. ЦР]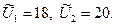
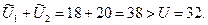
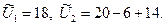
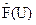 .
.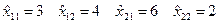 .
. Заметим, что суммарная полезность
Заметим, что суммарная полезность 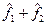 соответствует значению (35), уже найденному при определении нормативного коэффициента эффективности (см. рис. 11).
соответствует значению (35), уже найденному при определении нормативного коэффициента эффективности (см. рис. 11).



