
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторна робота № 3 «теплота змочування»Содержание книги
Поиск на нашем сайте
Перед тим, як приступити до лабораторної роботи з вивчення змочування твердих тіл рідинами, необхідно ознайомитися з такими поняттями: змочування, крайовий кут змочування, теплота змочування, коефіцієнт змочування.
Стислі теоретичні відомості Рідина може або розтікатися по поверхні твердого тіла, або збиратися на поверхні у вигляді крапель різної форми. Кут, який утворює крапля з поверхнею твердого тіла, називається крайовим кутом змочування та являє собою кількісну характеристику змочування (рис. 11). Чим менший крайовий кут, тим краще дана рідина змочує поверхню.
Рис. 11. Крайовий кут змочування Якщо крайовий кут змочування гострий (θ < 900), то поверхня добре змочується рідиною і називається ліофільною. Якщо крайовий кут тупий (θ > 900), то поверхня погано змочується рідиною і називається ліофобною. Тверді фази, що добре змочуються водою, називаються гідрофільними, а фази, що погано змочуються, ‑ гідрофобними. Гідрофільними матеріалами є оксиди, карбонати, сульфати, солі кисневмісних кислот, скло, целюлоза; гідрофобними – сірка, графіт, сульфіди металів, більшість полімерних матеріалів. Для порошкоподібних тіл визначення крайового кута змочування є неможливим, а тому характеристикою їхнього змочування може бути теплота змочування. Теплотою змочування називається кількість теплоти, яка виділяється при зануренні твердої фази у рідину. Для порошкоподібних речовин теплоту змочування відносять до одиниці маси (1 г або 1 кг) матеріалу і називають інтегральною теплотою змочування. Теплота змочування дорівнює зменшенню поверхневої енергії твердого тіла при перенесенні його з повітря або з вакууму в рідину. Вона завжди є від’ємною, тобто змочування супроводжується виділенням більшої або меншої кількості теплоти. Для гідрофільних фаз екзотермічність процесу змочування водою більша, ніж при змочуванні вуглеводнями, а для гідрофобних – навпаки. Характеристикою міри гідрофільності поверхні матеріалу є відношення теплот змочування матеріалу водою Q1 та неполярною рідиною Q2: Робота 3.1.Визначення природи поверхні гідрофільних та гідрофобних речовин калориметричним методом Метою роботи є кількісне визначення гідрофільності або гідрофобності порошків шляхом калориметричних вимірювань змочування їхніх поверхонь розчинниками різної природи та обчислення коефіцієнтів змочування b. Визначення проводиться в широкій пробірці, яку розташовано у термосі. Пробірка закриваться пробкою, в якій закріплено термометр Бекмана (точність вимірювання ±0,01 0С) та мішалку. Прилад для визначення теплових ефектів процесів називається калориметром. 1. З метою визначення теплоємності калориметра мірним циліндром відміряти в калориметричну пробірку 30 см3 дистильованої води та точно (±0,001 г) зважити на аналітичних терезах ~ 1 г KCl. 2. Перемішуючи воду мішалкою, зробити 6 вимірів температури з інтервалом 30 секунд за умови встановлення рівномірного ходу температури (температура після кожного вимірювання зростає або зменшується на одну й ту ж величину) і записати в табл. 3.1.
Таблиця 3.1. Результати вимірювань температури при змочуванні речовин
3. Всипати наважку KCl та енергійно перемішати, продовжуючи записувати температуру в табл. 3.1 з такими самими інтервалами часу (ще 5–7 вимірів після встановлення рівномірного ходу температури). Покази термометра Бекмана упродовж дослідів записувати в табл. 3.1. 4. Побудувати графік температурного ходу для точного визначення DТ з урахуванням теплообміну з оточуючим середовищем (рис. 12). Стрибок температури DТ визначити екстраполяцією прямих АВ та CD на середину головного періоду ВС.
Рис.12. Графік для визначення зміни температури DT при розчиненні KCl На графіку відрізок АВ – попередній період, CD – заключний період, ВС – головний період, тривалість якого визначається крайніми точками В і С, де рівномірний хід температури переривається. 5. Розраховувати теплоємність калориметра Ск (Дж/К) за формулою:
де а – наважка солі, г; M – молярна маса KCl, г/моль; QKCl –теплота розчинення KCl, яка складає 17500 Дж/моль; r – густина води, г/см3; С – питома теплоємність води, Дж/(г×К). 6. Вилити розчин солі та помити пробірку. 7. На технічних терезах зважити по дві наважки крохмалю та активованого вугілля масою 2 г кожна. 8. У вимиту калориметричну пробірку мірним циліндром налити 30 см3 дистильованої води. Перемішуючи воду мішалкою, зробити 5 –7 вимірів температури з інтервалом 30 с після встановлення рівномірного ходу температури. Всипати в пробірку крохмаль та, інтенсивно перемішуючи вміст пробірки, продовжувати записувати температуру з такими самими інтервалами часу до встановлення рівномірного температурного ходу, після чого зробити ще 5–7 вимірів. Вилити суспензію та помити пробірку. 9. Аналогічні операції провести з активованим вугіллям. Вилити суспензію вугілля і води та помити пробірку. Витерти пробірку насухо фільтрувальним папером. 10. У висушену калориметричну пробірку мірним циліндром налити 30 см3 бензолу. Перемішучи бензол мішалкою, зробити 6 вимірів температури з інтервалом 30 с після встановлення рівномірного ходу температури. Засипати в пробірку активоване вугілля і провести вимірювання, аналогічні попереднім дослідам змочування водою. Вилити суспензію вугілля і бензолу у посуд для зливів (у витяжній шафі) та сполоснути пробірку бензолом. 11. Аналогічні операції провести для дослідження змочування крохмалю бензолом. 12. Побудувати графіки зміни температури з часом для визначення DT. Розраховані значення записати в табл. 3.1. 13. Розрахувати теплоти змочування за формулою, Дж:
де V – об’єм рідини, см3; r – густина рідини, г/см3; C – питома теплоємність рідини, Дж/(г∙К); Ск – теплоємність калориметра, Дж/К; DT – зміна температури в ході досліду. При розрахунках теплот змочування у рівняння (3.2) слід підставляти властивості (r, C) досліджуваної рідини. Результати вимірювань записати в табл. 3.1. 14. Розрахувати величини коефіцієнтів змочування крохмалю та активованого вугілля як відношення теплот змочування відповідних матеріалів водою та бензолом: Звіт Таблиця 3.1 Графіки T = f(t) для розчинення KCl у воді та змочування досліджуваних порошків рідинами (всього 5 графіків). Теплоємність калориметра Ск =....... Дж/К. Значення коефіцієнтів змочування bкрохмалю =..............; bвугілля =............ Висновок. Питання до лабораторної роботи 1. Як і для чого визначають теплоємність калориметра? 2. Які особливості вимірювання температури термометром Бекмана? 3. Як визначають теплоти змочування порошків? 4. Як і навіщо визначають коефіцієнти змочування порошків? 5. Яка з досліджених Вами речовин є гідрофільною? Чому? 6. Яка з досліджених Вами речовин є гідрофобною? Чому? 7. Як змінити характер поверхні з гідрофільного на гідрофобний і навпаки? Література: [1] 153 – 168; [2] 72 – 89; [3] 78 – 99; [4] 44 – 50. Лабораторна робота № 4«СЕДИМЕНТАЦІЯ» Перед виконанням лабораторної роботи з седиментаційного аналізу суспензій треба засвоїти принципи побудови седиментаційної кривої та методику розрахунку розмірів часток в залежності від швидкості їхнього осідання. Необхідно знати межі застосування методу седиментаційного аналізу, вміти аналізувати седиментаційні криві моно-, ди-, три- та полідисперсних суспензій.
Стислі теоретичні відомості Седиментаційний аналіз – це метод визначення розмірів часток та фракційного складу дисперсних систем за допомогою безперервного зважування осаду. На сферичну частку, що осідає у в’язкому середовищі, діють три сили: спрямована вниз сила тяжіння
і після нескладних спрощень перетворюється на вираз:
де u – швидкість осідання частинки, м/с; r та Рівняння (4.1) можна використовувати для визначення розмірів часток дисперсної фази, що седиментує, якщо відомі характеристики дисперсійного середовища
Якщо в рівнянні (4.2) всі постійні за умови досліду величини об’єднати в одну константу
Швидкість осідання часток можна визначити експериментально, якщо відомі висота Знаючи Для полідисперсних систем седиментаційний аналіз проводять методом безперервного зважування осаду при седиментації. За даними, що одержані експериментально, будують седиментаційну криву – залежність маси часток Розглянемо спочатку процес осадження монодисперсної суспензії, частки якої мають однакові розміри і осідають з рівними швидкостями. За однакової концентрації часток в кожній точці суспензії кількість частинок, що осідають за одиницю часу на шальку терезів, є незмінною, тому залежність
Рис. 13. Седиментаційна крива монодисперсної суспензії
Якщо суспензія є бідисперсною, тобто містить частинки тільки двох різних розмірів, то процес їх осадження можна розглядати як одночасне осадження двох монодисперсних фаз (рис. 14).
Рис. 14. Седиментаційна крива бідисперсної суспензії
Осідання фракції більших за розміром частинок описується прямою OB, менших за розміром – прямою OC; сумісне осідання обох фракцій описується лінією OBC, що є геометричною сумою OB та OC. Точки зламу на лінії OBCK відповідають моментам повного осідання великих (точка В, τ1) та малих (точка С, τ2) частинок. За цими точками можна обчислити швидкості осідання частинок За кривою седиментації можна визначити і масу кожної фракції. З рис. 14 видно, що відрізок Q1 на осі ординат відповідає масі фракції великих часток, а відрізок Q2 – масі фракції малих за розміром часток. Поширивши ці міркування на полідисперсні системи, що складаються з великого числа фракцій, кожна з яких містить частинки однакового розміру, можна дійти висновку, що для таких систем графік седиментації зображується ламаною лінію з певним числом точок перегину. Дійсно, зазвичай експериментальна седиментаційна крива не є плавною кривою, а являє собою ламану лінію, що складається з прямолінійних ділянок (рис. 15, лінія OABCDEF). Як правило, на цій лінії можна виділити 5 – 6 відрізків, наявність яких свідчить про те, що дисперсна фаза складається з кількох фракцій.
Рис. 15. Крива седиментації полідисперсної суспензії
Шляхом екстраполяції кожного з лінійних відрізків на вісь ординат можна розділити загальну масу частинок, що осідають, на фракції. Маси фракцій визначаються довжиною відрізків, які відтинаються на осі ординат Q подовженнями лінійних фрагментів ламаної OABCDEF (відрізки ОА,АВ, ВСі подалі відповідають масам фракцій Q 1, Q 2, Q 3 і т. д.). Якщо прийняти величину відрізка OF (Q) за 100%, то за величинами відрізків Q 1, Q 2, Q 3 і т. д можна розрахувати масовий відсоток кожної фракції у суспензії:
Очевидно, що q1 + q2 +... + qn = 100 %. Час осідання фракції з частинками певного розміру визначається координатою відповідної точки зламу кривої OABCDEF на осі абсцис (для т. А – τ 1, для т. В – τ 2 тощо). За значеннями За результатами математичної обробки седиментаційної кривої будують диференціальну криву розподілу часток за розмірами
Рис. 16. Диференціальна крива розподілу часток за розмірами
Наведена на рис. 16 крива показує поширеність частинок у дисперсній системі залежно від їхнього розміру.Максимум на цій кривій відповідає фракції з частинками радіусу
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.233.83 (0.008 с.) |


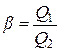 , яке називається коефіцієнтом змочування. Для гідрофільних тіл b > 1, для гідрофобних – b < 1.
, яке називається коефіцієнтом змочування. Для гідрофільних тіл b > 1, для гідрофобних – b < 1.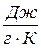
 , см3
, см3

 ,
,
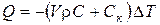 , (3.2)
, (3.2) і зробити висновок про природу речовин.
і зробити висновок про природу речовин. та дві сили, спрямовані вгору: сила Архімеда
та дві сили, спрямовані вгору: сила Архімеда  і сила в’язкого опору (сила Стокса)
і сила в’язкого опору (сила Стокса)  . За умови рівноваги сил, що діють на частинку, вона рухається рівномірно та прямолінійно. Швидкість руху частинки можна визначити за рівнянням, що описує спільну дію трьох сил
. За умови рівноваги сил, що діють на частинку, вона рухається рівномірно та прямолінійно. Швидкість руху частинки можна визначити за рівнянням, що описує спільну дію трьох сил
 ,
,
 – відповідно густина дисперсної фази та дисперсійного середовища, кг/м3; g – прискорення сили тяжіння, м/с2;
– відповідно густина дисперсної фази та дисперсійного середовища, кг/м3; g – прискорення сили тяжіння, м/с2;  – в’язкість дисперсійного середовища, Па·с; r – еквівалентний радіус сферичної частинки, м.
– в’язкість дисперсійного середовища, Па·с; r – еквівалентний радіус сферичної частинки, м. , а також швидкість осідання часток
, а також швидкість осідання часток  , перетворивши його на формулу для розрахунків радіусів часток дисперсної фази:
, перетворивши його на формулу для розрахунків радіусів часток дисперсної фази: .
.
 , то воно набуває вигляду
, то воно набуває вигляду .
.
 та час
та час 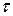 їхнього осідання як
їхнього осідання як  .
. , за рівнянням (4.3) можна обчислити еквівалентні радіуси часток, що осідають за певні інтервали часу.
, за рівнянням (4.3) можна обчислити еквівалентні радіуси часток, що осідають за певні інтервали часу. , що осіли, від часу осідання τ. Потім експериментальну криву обробляють графічно для побудови диференціальної кривої розподілу часток за розмірами.
, що осіли, від часу осідання τ. Потім експериментальну криву обробляють графічно для побудови диференціальної кривої розподілу часток за розмірами.

 та
та  і, відповідно, їх радіуси r1 та r2.
і, відповідно, їх радіуси r1 та r2.
 .
.
 та
та  розраховують мінімальні та максимальні значення радіусів частинок даної суспензії.
розраховують мінімальні та максимальні значення радіусів частинок даної суспензії. (рис. 16). Оскільки частинки певної фракції мають фіксований радіус, то величину
(рис. 16). Оскільки частинки певної фракції мають фіксований радіус, то величину  розраховують за формулою
розраховують за формулою  для всіх радіусів, крім найбільшого
для всіх радіусів, крім найбільшого  = rmax та найменшого rn = rmіn. Для фракцій найкрупніших та найдрібніших частинок величини
= rmax та найменшого rn = rmіn. Для фракцій найкрупніших та найдрібніших частинок величини  та
та  .
.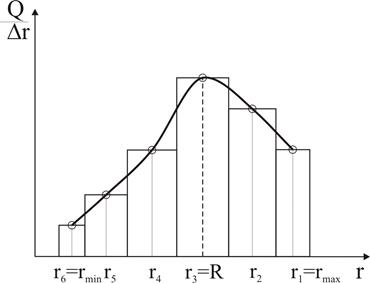
 , яку називають переважною, тому що масовий вміст цієї фракції у системі найбільшій. Радіус
, яку називають переважною, тому що масовий вміст цієї фракції у системі найбільшій. Радіус 


