
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение тесноты связи между атрибутивным признакамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками. Для этого статистической наукой разработаны методы, которые называются непараметрическими.
Коэффициент взаимной сопряженности Чупрова и Пирсона Коэффициент взаимной сопряженности Чупрова и Пирсона применяется тогда, когда исследуется теснота связи между варьированием двух атрибутивных признаков, когда это варьирование образует 3 и более группы по каждому признаку. Коэффициенты принимают значения от 0 до 1, и чем ближе к 1, тем теснее связь. Этот метод обычно используется для установления характера связи при относительно небольшом числе наблюдений. С помощью этого приема можно дать самую общую характеристику связи посредством сравнения факторного и результативного признаков. Коэффициент взаимной сопряженности Пирсона вычисляется по формуле:
где φ2 – показатель взаимной сопряженности. Коэффициент взаимной сопряженности Чупрова вычисляется по следующей формуле:
где φ2 – показатель взаимной сопряженности, m1 – количество групп по первому признаку, m2 – количество групп по второму признаку. Коэффициент Чупрова всегда меньше коэффициента Пирсона. Он дает обычно более осторожную оценку связи.
Пример: (для нахождения показателя взаимной сопряженности). Таблица 10.1 – Распределение предприятий по техническому и организационному уровню развития
1) Каждую частоту возведем в квадрат и запишем соответствующий результат в скобках. 2) Делим число, стоящее в скобках, на величину в итоговой строке. 3) Числа, полученные во втором пункте, складываем по строкам и записываем в графу «Итого»: 3,27+3,2+5,6=12,07. 4) В графе «Итого» делим второе число на первое и результат записываем в эту же графу: 12,07/25=0,4898. 5) Результаты, полученные в 4-м пункте, складываем и записываем в правом нижнем углу таблицы. φ2= 1,0958-1=0,0958 – показатель взаимной сопряженности.
Связь незначительная. Коэффициенты ассоциации и контингенции Коэффициенты ассоциации и контингенции применяются тогда, когда исследуется связь между варьированием двух атрибутивных признаков, по каждому признаку имеется две группы (таблица 10.2).
Таблица 10.2 – Варьируемые атрибутивные признаки
Коэффициент ассоциации вычисляется по формуле
Коэффициент контингенции вычисляется
Коэффициенты контингенции и ассоциации принимают значение от -1 до 1, показывают не только тесноту, но и направление связи. Если коэффициент >0, связь прямая, <0 – обратная. Чем ближе коэффициент к ±1, тем связь теснее. Коэффициент контингенции всегда меньше коэффициента ассоциации. Он дает более осторожную оценку тесноты связи.
Измерение тесноты связи между количественными признаками Методы измерения связи между количественными признаками не могут обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических (корреляционных и дисперсионных). Метод сравнения параллельных рядов Установить наличие и характер связи между количественными признаками можно с помощью метода сравнения параллельных рядов, заключающегося в следующем. Признаки-факторы мы располагаем в возрастающем или убывающем порядке в зависимости от целей исследования и рядом записываем соответствующий результативный признак. Затем путем сопоставления двух параллельных рядов делаем предположение о наличии связи и ее направлении.
Пример: Находим зависимость между производительностью труда (у) и энерговооруженностью (х), имея данные по 25-и заводам.
Коэффициент Фехнера Коэффициент Фехнера основан на методе параллельных рядов. Суть его в том, что сравниваются знаки отклонений значений признака от их средних арифметических. 1) Находим средние арифметические
2) Рассмотрим совпадение и несовпадение знаков отклонений. Совпадение знаков (С) означает согласованную вариацию, а несовпадение (Н)- нарушение этой согласованности. С =21, Н =4. Коэффициент Фехнера вычисляется по формуле
Принимает значения от –1до +1. Вычисляем:
Связь прямая и заметно согласованная. Коэффициент Фехнера примитивен, т.к. улавливает только направление связи и не учитывает ее величину.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.149.174 (0.007 с.) |


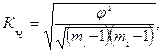
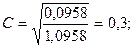
 .
.



 .
. .
.


