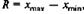Новые инструменты управления качеством

Среди простых статистических методов и инструментов, названных так ввиду их сравнительной несложности, убедительности и доступности, наибольшее распространение получили семь методов, выделенных в начале 50-х гг. японскими специалистами под руководством К. Исикавы.

В своей совокупности они образуют эффективную систему методов контроля и анализа качества. С их помощью, по свидетельству самого К. Исикавы, может решаться до 95 % всех проблем, находящихся в поле зрения производственников. Согласно К. Исикаве, в число семи простых методов входят: контрольный листок, гистограмма, расслоение (стратификация) данных, причинно-следственная диаграмма Исикавы, диаграмма Парето, диаграмма разброса и контрольная карта.

Рассматриваемые в данной главе инструменты часто называют «семь простых японских статистических методов контроля, анализа и управления качеством». Использование слова «статистические» в названии обусловлено тем фактом, что большинство этих методов-инструментов предназначено для работы с числовыми (статистическими) данными, собранными в ходе контроля и управления процессом. Исключением является только четвертый метод-инструмент — «Причинно-следственная диаграмма Исикавы», оперирующий преимущественно с вербальной (представленной в словесной форме) информацией.

Контрольный листок

Контрольный листок — это форма для систематического сбора данных и автоматического их упорядочения с целью облегчения дальнейшего использования собранной информации.

Контрольный листок — это бумажный бланк, на котором заранее напечатаны названия и диапазоны контролируемых показателей, с тем чтобы можно было легко и точно записать данные измерений и упорядочить их для дальнейшего использования. Этот инструмент (контрольный листок) служит средством для сбора и упорядочения первичных данных. Он используется для получения ответа на вопрос «Как часто встречаются изучаемые события?».

Применяются следующие виды контрольных листков:

• контрольный листок для регистрации измеряемого параметра в ходе производственного процесса;

• контрольный листок для регистрации видов несоответствий;

• контрольный листок для оценки воспроизводимости и работоспособности технологического процесса и т. п.

Форма контрольного листка разрабатывается в соответствии с конкретной ситуацией. В любом случае в нем указываются:

• объект изучения (например, наименование и/или чертеж изделия или детали);

• таблица регистрации данных о контролируемом параметре (например, линейный размер изделия или детали);

• место контроля (цех, участок);

• должность и фамилия работника, регистрирующего данные;

• дата сбора данных;

• продолжительность наблюдения и наименование контрольного прибора (если он применяется в ходе наблюдения).

В регистрационной таблице в соответствующей графе проставляются точки, черточки, крестики и другие условные знаки, соответствующие количеству наблюдаемых событий. Например, при регистрации количества событий могут быть использованы следующие символы:

Таблица - Регистрация событий

Диапазон применения контрольных листков очень широк, а их виды весьма разнообразны. При подготовке контрольных листков нужно следить за тем, чтобы использовались наиболее простые способы их заполнения (цифры, условные значки), число контролируемых параметров было по возможности наименьшим, а форма листка была проста для заполнения и анализа. Бланки контрольных листков должны быть напечатаны на бумаге, исключающей расплывание чернил, и иметь удобный для хранения и использования формат.

В качестве примеров контрольных листков можно назвать:

• график температуры больного;

• контрольный листок для сбора данных об отказавших деталях телевизоров;

• контрольный листок для сбора информации о дефектах при производстве тентовых материалов и т. д.

Ниже приведены примеры контрольных листков для сбора информации.

По результатам сбора данных, произведенным для нескольких партий с использованием рассмотренного выше контрольного листка, может быть составлена сводная таблица.

Гистограмма

Гистограмма - это инструмент, позволяющий зрительно оценить закон распределения величины разброса данных, а также принять решение о том, на чем следует сфокусировать внимание для целей улучшения процесса.

Гистограмма отображается серией столбиков одинаковой ширины, но разной высоты. Ширина столбика представляет интервал в диапазоне наблюдений, высота — количество наблюдений (измерений), попавших в данный интервал. При нормальном законе распределения данных существует тенденция расположения большинства результатов наблюдений ближе к центру распределения (к центральному значению) с постепенным уменьшением при удалении от центра.

Построение гистограммы, как правило, включает в себя следующие этапы.

1. Разработка формы контрольного листка для сбора первичных данных. Пример такого контрольного листка для процесса производства валиков приведен ниже.

2. Сбор статистических данных xi, i = 1, 2,..., N, характеризующих ход процесса, и заполнение второго столбца контрольного листка. После заполнения контрольного листка приступают собственно к построению гистограммы.

3. Вычисление диапазона данных (выборочного размаха)

где xmax — наибольшее наблюдаемое значение; xmin — наименьшее наблюдаемое значение.

В нашем случае xmax = 10,020 мм, xmin = 9,985 мм, т. е. R = 10,020 - 9,985 = 0,035 мм = 35 мкм.

4. Определение количества интервалов п на гистограмме часто осуществляют по формуле Стерджесса

n ≈ l + 3,322 1g N,

где N — общее количество собранных данных в выборке.

Рекомендуемое число интервалов гистограммы, которое получается при использовании формулы Стерджесса, представлено в таблице.

 

 

Таблица - К выбору рекомендуемого числа интервалов на гистограмме

По данным рассматриваемого нами контрольного листка N = 88, соответственно п = 1 + 3,322 lg 88 = 7,46 - 7.

5. Определение размеров интервалов осуществляют так, чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины. Для получения ширины интервалов h = R/n размах R делят на полученное выше количество интервалов п.

В нашем случае h = 0,035 мм / 7 = 0,005 мм = 5 мкм.

Желательно, чтобы размер интервала был не менее двух делений шкалы измерительного прибора (в рассматриваемом примере данные контрольного листка были получены с использованием микрометрической головки часового типа с ценой деления 1 мкм, т. е. один интервал соответствует пяти делениям шкалы прибора).

6. Определение границ интервалов.

Сначала определяют нижнюю границу первого интервала и прибавляют к ней ширину этого интервала, чтобы получить границу между первым и вторым интервалами. Далее продолжают прибавлять найденную ширину нтервала h к предыдущему значению для получения второй границы, затем третьей и т. д. После завершения такой работы можно удостовериться, что верхняя граница последнего интервала совпадает с аксимальным значением хmах.

7. Вычисление частот.

В третий столбец таблицы контрольного листка вносят количество кi аликов, попавших в каждый интервал. По результатам наблюдений, отмеченных черточками во втором столбце этой таблицы, подсчитывают общее количество наблюдений (в нашем случае N = 88), а затем в четвертый столбец записывают относительные частоты, выраженные в процентах и подсчитанные по формуле

8. Построение горизонтальной и вертикальной осей графика.

Берется миллиметровая бумага, на ней наносятся горизонтальная и вертикальная оси, а затем на каждой оси выбираются масштабы.

9. Построение графика гистограммы.

На горизонтальную ось необходимо нанести границы интервалов. На оси абсцисс с обеих сторон (перед первым и после последнего интервалов) следует оставить место, не менее размера одного интервала. Пользуясь шириной интервалов как основанием, строят прямоугольники, высота каждого из которых равна частоте попадания результатов наблюдений в соответствующий интервал. На график (см. рис. 4.5.3) наносят линию, представляющую среднее арифметическое значение «х», а также линии, представляющие границы поля допуска, если они имеются.

Полезную информацию о характере распределения случайной величины можно получить, взглянув на форму гистограммы. Формы, представленные на рис. типичны, и вы можете воспользоваться ими как образцами при анализе процессов.

а — симметричная, или колоколообразная;

б — гребенка;

в — положительно скошенное распределение;

г — распределение с обрывом справа;

д — равномерное распределение (плато);

е — двухпиковая (бимодальная) форма.

Рисунок - Основные формы гистограмм:

Обычная форма (симметричная, или колоколообразная). Среднее значение гистограммы приходится на середину размаха данных. Наивысшая частота оказывается в середине и постепенно снижается к обоим концам. Форма симметрична.

Гребенка Интервалы через один имеют более низкие (высокие) частоты.

Такая форма встречается, когда число единичных наблюдений, попадающих в интервал, колеблется от интервала к интервалу или когда действует определенное правило округления данных.

Положительно скошенное распределение (отрицательно скошенное распределение). Среднее значение гистограммы локализуется слева (справа) от центра размаха. Частоты довольно резко спадают при движении влево (вправо) и, наоборот, медленно — при движении вправо (влево). Форма асимметрична.

Распределение с обрывом справа (распределение с обрывом слева). Среднее арифметическое гистограммы локализуется далеко слева (справа) от центра размаха. Частоты резко спадают при движении влево (вправо) и, наоборот, медленно вправо (влево). Форма асимметрична.

Это одна из тех форм, которые часто встречаются при 100 %-ной разбраковке изделий из-за плохой управляемости процесса, а также когда проявляется резко выраженная положительная (отрицательная) асимметрия.

Равномерное или прямоугольное распределение (плато). Частоты в разных интервалах образуют плато, поскольку все интервалы имеют более или менее одинаковые ожидаемые частоты. Такая форма встречается в смеси нескольких распределений, имеющих различные средние значения.

Двухпиковая (бимодальная) форма. В окрестностях центра диапазона данных частота низкая, т. е. по пику с каждой стороны.

Метод стратификации (группировки, расслоения) статистических данных

Стратификация — разделение полученных данных на отдельные группы (слои, страты) в зависимости от выбранного стратифицирующего фактора.

В качестве стратифицирующего фактора могут быть выбраны любые параметры, определяющие особенности условий возникновения и получения данных:

• различное оборудование;

• операторы, производственные бригады, участки, цехи, предприятия и т. п.;

• время сбора данных;

• разные виды сырья;

• различие используемых станков, средств измерения и т. д.

При отсутствии учета стратифицирующего фактора (расслоения данных) происходит их объединение и обезличивание, затрудняющее установление действительной взаимосвязи между полученными данными и особенностями их возникновения.

Например, при анализе источника дефектной продукции, поставляемой предприятию несколькими сторонними поставщиками, целесообразно в качестве стратифицирующего фактора выбрать поставщиков и произвести стратификацию дефектной продукции по поставщикам.

В японских журналах, посвященных работе кружков качества, неоднократно публиковались статьи о повышении качества продукции после многократного (до 50-80 раз) применения метода стратификации для анализа проблем, возникавших в производственных процессах.

Причинно-следственная диаграмма Исикавы

Результат процесса построения причинно-следственной диаграммы Исикавы зависит от многочисленных факторов, между которыми существуют отношения типа «причина — результат». Мы можем определить структуру или характер этих многофакторных отношений благодаря систематическим наблюдениям. Трудно решить сложные проблемы, не зная этой структуры, которая представляет собой цепь причин и результатов. Диаграмма причин и результатов — средство, позволяющее выразить эти отношения в простой и доступной форме.

В 1953 г. профессор Токийского университета Каору Исикава, обсуждая проблему качества на одном заводе, суммировал мнение инженеров в форме диаграммы причин и результатов. Она получила название «схема Исикавы» (в японской литературе эту диаграмму из-за формы часто именуют «рыбья кость» или «рыбий скелет»).

При построении диаграммы Исикавы рекомендуется придерживаться следующего порядка действий.

1. Определите перечень показателей качества (видов неудач, дефектов, брака), которые следует проанализировать.

2. Выберите один показатель качества и напишите его в середине правого края чистого листа бумаги. Слева направо проведите прямую линию, которая будет представлять собой «хребет» будущей диаграммы Исикавы.

3. Запишите главные причины, влияющие на показатель качества;

4. Соедините линиями («большими костями») главные причины с «хребтом», расположив основные из этих главных причин ближе к голове «рыбьего скелета».

5. Определите и запишите вторичные причины для уже записанных главных причин.

6. Соедините линиями («средними костями») вторичные причины с «большими костями».

7. Проверьте логическую связь каждой причинной цепочки.

8. Нанесите всю необходимую информацию (надписи) и проверьте законченность составленной причинно-следственной диаграммы Исикавы.

Несмотря на относительную простоту, построение диаграммы Исикавы требует от ее исполнителей хорошего знания объекта анализа и понимания взаимозависимости и взаимовлияния факторов.

Часто построение диаграммы сопровождается «мозговым штурмом». Это прекрасный метод приведения в действие творческого мышления группы для быстрого формулирования, разъяснения и оценки значительного перечня идей, проблем, причин, вопросов. Правила проведения «мозгового штурма (атаки)».

Рисунок - Пример причинно-следственной диаграммы Исикавы.

При практическом построении причинно-следственной диаграммы советуем воспользоваться следующими рекомендациями:

1. Определите все факторы, имеющие отношение к рассматриваемой проблеме, путем наблюдений и опроса многих людей.

Из всех факторов, указанных на диаграмме, надо выделить те, которые оказывают наибольшее воздействие на показатель качества. Если на первоначальной стадии, еще до построения диаграммы, из вашего поля зрения выпал какой-то фактор, он не появится на более поздней стадии.

Поэтому чрезвычайно важно на стадии подготовки диаграммы привлечь к обсуждению как можно больше людей, чтобы диаграмма была полной и в ней ничего не было упущено.

2. Сформулируйте показатель как можно точнее.

Если показатель сформулирован абстрактно, то будет построена диаграмма, основанная на общих соображениях. И хотя она будет правильной с точки зрения отношений «причина — результат», в ней будет мало проку при решении конкретных проблем.

3. Воспользуйтесь разными классификациями (стратификацией) причин и постройте столько диаграмм причин и результатов, сколько показателей вы хотите исследовать.

Например, ошибки в весе и в размерах одного и того же изделия нужно анализировать с помощью двух разных диаграмм, так как их структуры в этом случае будут различными. Попытка объединить эти две диаграммы в одну приведет к тому, что она окажется большой и сложной, практически бесполезной, что только затруднит процесс принятия решений.

4. При построении диаграммы Исикавы старайтесь выбирать такие показатели качества и такие факторы, которые можно измерить. После составления диаграммы причин и результатов надо с помощью объективных данных оценить силу отношений «причина — результат». Чтобы это стало возможным, и показатель качества, и факторы, на него влияющие, должны быть измеримыми. Если их невозможно измерить, надо все-таки попытаться это сделать или найти показатели-заменители.

5. Отыщите факторы, по которым надлежит принять меры.

Если по обнаруженной причине нельзя предпринять никаких действий, то проблема неразрешима. Чтобы процесс совершенствования стал эффективным, надо разбивать причины на подпричины до тех пор, когда по каждой из них можно предпринять действия по устранению причин дефектов (по улучшению качества), иначе сам процесс их выявления превратится в бессмысленное упражнение.

Диаграмма Парето

Диаграмма Парето — разновидность столбиковой диаграммы, применяемой для наглядного отображения рассматриваемых факторов в порядке уменьшения (возрастания) их значимости. Эта диаграмма является инструментом, позволяющим распределить усилия для разрешения возникающих проблем и выявить главные причины, с которых надо начинать действовать, например, позволяет точно определить и квалифицировать основные виды причин брака при диагностировании процесса; установить, борьба с какими видами причин брака позволит наиболее эффективно и быстро повысить качество продукции.

В 1897 г. итальянский экономист В. Парето (1845—1923) установил, что примерно 70—80 % доходов или благ в государстве в большинстве случаев принадлежит 20—30 % населения. Американский экономист М. Лоренц в 1907 г. независимо от Парето пришел к тому же выводу, осуществив дальнейшее развитие идей Парето (помимо так называемой столбиковой диаграммы им было предложено использовать кумулятивную кривую, которую часто называют кривой Лоренца). Идея применения этой диаграммы для анализа причин возникновения брака и путей повышения качества принадлежит Дж. Джурану

Этапы построения диаграммы Парето

Рекомендуется порядок построения диаграммы Парето, включающий в себя следующие этапы:

1. Решите, какие проблемы надлежит исследовать и как собирать данные, в частности:

1) какого типа проблемы вы хотите исследовать?

Например: дефектные изделия, потери в денежном выражении, несчастные случаи;

2) какие данные надо собрать и как их классифицировать?

Например: по видам дефектов, месту их появления, процессам, рабочим;

3) какой метод следует применить и каков период сбора данных.

Пусть с использованием «мозговой атаки» построена диаграмма Исикавы и установлено N причин, вызывающих брак. Возникает вопрос: с какой из этих причин надо начинать бороться в первую очередь, чтобы наиболее эффективно повысить качество? Для ответа на этот вопрос и следует использовать диаграмму Парето, например так, как это рассмотрено ниже.

2. Разработайте контрольный листок для регистрации данных (о частоте возникновения дефектов в зависимости от вызывающих их причин) с перечнем видов собираемой информации.

3. Заполните контрольный листок регистрации данных и подсчитайте необходимые итоговые данные.

4. Для построения диаграммы Парето разработайте бланк для обработки статистических данных, имеющихся в контрольном листке. В этой таблице следует предусмотреть графы для регистрации:

• числа зарегистрированных дефектов каждого типа как в единицах их измерения, так и в процентах к общему количеству дефектов;

• накопленной суммы числа дефектов, выраженной в единицах измерения дефектов;

• накопленной суммы числа дефектов, выраженной в процентах к общему итогу (накопленного процента).

5. Заполните таблицу, расположив данные, полученные по каждому проверяемому признаку (типу дефекта), в порядке убывания их значимости.

Группу «прочие» надо поместить в последнюю строку таблицы вне зависимости от того, насколько большим получилось число, так как ее составляет совокупность признаков, числовой результат по каждому из которых меньше, чем самое маленькое значение, полученное для признака, выделенного в отдельную строку.

6. Начертите одну горизонтальную и две вертикальные оси:

1) сначала постройте горизонтальную ось. Разделите эту ось на интервалы в соответствии с числом контролируемых признаков (типов дефектов);

2) затем постройте вертикальные оси с левой и правой стороны графика:

• на левую ось нанесите шкалу с интервалами (делениями) от 0 до числа, соответствующего общему итогу (суммарному числу дефектов);

• на правую ось нанесите шкалу с интервалами (делениями) от 0 до 100 %.

7. Постройте столбиковую диаграмму.

Рисунок - Диаграмма Парето по видам пороков тентового материала:

8. Начертите кумулятивную кривую (кривую Лоренца).

На вертикалях, соответствующих правым концам каждого интервала на горизонтальной оси, нанесите точки накопленных сумм (результатов или процентов) и соедините отрезками прямых.

9. Нанесите на диаграмму все обозначения и надписи:

• надписи, касающиеся диаграммы (название, разметка числовых значений на осях);

• надписи, касающиеся данных;

• сведения о месте и времени сбора и обработки данных;

• сведения о персонале, принимавшем участие в работе;

• любые другие сведения, которые могут быть полезными в последующей работе с построенной диаграммой Парето.

Определяющим достоинством диаграммы Парето является то, что она дает возможность разгруппировать факторы на значительные, т. е. встречающиеся наиболее часто, и на незначительные, т. е. встречающиеся относительно редко.

Диаграмма Парето показывает в убывающем порядке относительное влияние каждой причины на общую проблему.

После проведения корректирующих мероприятий диаграмму Парето можно вновь построить для изменившихся в результате коррекции условий и проверить эффективность проведенных улучшений. В сложной экономической жизни предприятия проблемы могут возникнуть в любой момент в любом подразделении. Анализ этих проблем всегда целесообразно начинать с составления диаграммы Парето.

Диаграмма разброса (рассеивания)

На практике часто важно изучить зависимости между парами каких-либо переменных. Как можно, например, установить, зависит ли вариация размеров детали от изменений скорости вращения шпинделя токарного станка? Или, допустим, мы хотим управлять концентрацией материала, но предпочитаем заменить измерение концентрации измерением плотности, поскольку на практике гораздо легче мерить. Для изучения зависимостей между двумя переменными, такими как скорость вращения шпинделя токарного станка и размер детали (или концентрация и плотность), мы можем воспользоваться так называемой диаграммой рассеивания.

Диаграмма разброса (рассеивания) — инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.

Этапы построения диаграммы разброса (рассеивания)

Можно рекомендовать следующий порядок построения диаграммы разброса (рассеивания).

1. Соберите парные данные (х, у), между которыми вы хотите исследовать зависимость, и расположите их в табл. 4.5.5. Было бы хорошо иметь по меньшей мере 30 пар данных.

2. Найдите максимальные и минимальные значения для х и у. Выберите шкалы на горизонтальной и вертикальной осях так, чтобы обе длины рабочих частей осей х н у получились приблизительно одинаковыми (чтобы они уместились на экране компьютера или на стандартном листе бумаги), тогда диаграмму будет легче читать. При определении масштабов возьмите на каждой оси от 3 до 10 градационных делений и при обозначении этих делений используйте (для облегчения чтения) круглые числа. Если одна переменная — фактор, а вторая — характеристика качества, то выберите для фактора горизонтальную ось х, а для характеристики качества — вертикальную ось у.

3. На экране компьютера (на отдельном листе бумаги) начертите график и нанесите на него данные. Если в разных наблюдениях получаются одинаковые значения, покажите эти точки, либо рисуя концентрические кружки, либо нанося вторую точку рядом с первой.

4. Нанесите на диаграмму все необходимые обозначения, например:

а) название диаграммы;

б) интервал времени сбора данных;

в) число пар данных;

г) названия и единицы измерения для каждой оси;

д) дата составления диаграммы;

е) имя (и прочие данные) человека, который составлял эту диаграмму.

Убедитесь, что перечисленные выше данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто строил диаграмму.

а — сильная положительная корреляция;

б — сильная отрицательная корреляция;

в — слабая положительная корреляция;

г — слабая отрицательная корреляция;

д — криволинейная корреляция;

е — отсутствие корреляции.

Рисунок - Типичные виды диаграмм разброса (рассеивания):

Временные ряды

Временные ряды применяются, когда требуется самым простым способом представить ход изменения наблюдаемых данных за определенный промежуток времени.

Временнóй ряд предназначен для наглядного представления данных, он очень прост в построении и использовании. Точки наносятся на график в том порядке, в каком они были собраны. Поскольку они отображают изменение характеристики во времени, очень существенна последовательность данных.

Одно из наиболее эффективных применений временного ряда заключается в выявлении существенных тенденций или изменений как мгновенных (индивидуальных), так и средних значений величины, характеризующей качество продукции. Пример построения временного ряда представлен на примере анализа сбыта.

Рисунок - Сравнительный анализ сбыта продукции:

__________ 2000 г.; _ _ _ _ _ _ _ _ 2001 г.

Временные ряды могут быть очень полезны при интерпретации и анализе статистических данных. Рассмотрим один из интересных случаев, иллюстрирующих успешное применение временных рядов.

Контрольные карты

Контрольные карты - это представление полученных в ходе технологического процесса данных в виде точек (или графика) в порядке их поступления во времени. Они позволяют контролировать текущие рабочие характеристики процесса, показывают отклонения этих характеристик от целевого или среднего значения, а также уровень статистической стабильности (устойчивости, управляемости) процесса в течение определенного времени. Их можно использовать для изучения возможностей процесса, чтобы помочь определить достижимые цели качества и выявить изменения средних характеристик и изменчивость процесса, которые требуют корректирующих или предупреждающих действий.

Контрольные карты впервые были предложены в 1924 г. У. Шухартом с намерением исключить необычные вариации, т. е. отделять вариации, которые обусловлены определенными причинами, от тех, что вызваны случайными причинами.

Контрольные карты основываются на четырех положениях:

• все процессы с течением времени отклоняются от заданных характеристик;

• небольшие отклонения отдельных точек являются непрогнозируемыми;

• стабильный процесс изменяется случайным образом, но так, что группы точек этого процесса имеют тенденцию находиться в прогнозируемых границах;

• нестабильный процесс отклоняется в силу неслучайных факторов, и не случайными обычно считаются те отклонения, которые находятся за пределами прогнозируемых границ.

Контрольные карты позволяют использовать текущие данные процесса, чтобы установить статистически нормальные рабочие границы (границы регулирования), в которых должны находиться характеристики процесса.

Постоянное использование контрольной карты может помочь определить факторы, вызывающие отклонения процесса от заданных требований, и исключить их влияние.

Результаты измерений характеристики процесса в течение определенного времени сравниваются с требованиями к процессу для установления того, что контролируемая характеристика процесса:

• выходит за установленные границы поля допуска, но размах R (разброс параметров) процесса не превышает ширины поля допуска, что сохраняет возможность удовлетворить требования потребителя путем наладки или настройки процесса, например, за счет совмещения среднего арифметического значения «х» характеристики процесса с серединой поля допуска CL;

• выходит за установленные границы поля допуска, причем среднее значение «х» близко к середине поля допуска CL, а размах R (разброс параметров) процесса превышает ширину поля допуска, что не позволяет удовлетворить требования потребителя (необходимо улучшение процесса, а именно: уменьшение размаха R за счет использования более точного станка или уменьшения влияния внешних факторов, вызывающих повышенную изменчивость процесса);

• среднее значение «х» характеристики процесса далеко от середины поля допуска CL и величина размаха R превышает ширину поля допуска (для улучшения качества процесса требуется как его настройка/наладка, так и уменьшение размаха (разброса) характеристики процесса).

При разработке контрольной карты самым важным является способ определения контрольных границ. Для этого необходимо собрать большое количество данных (называемых предварительными данными), характеризующих состояние процесса, и на их основе рассчитать (по установленным формулам) контрольные границы. В производственной практике используются различные виды контрольных карт, отличающиеся друг от друга характером используемых данных.

Существуют два класса контрольных карт: один - для непрерывных значений, а второй — для дискретных. Сведения об основных типах контрольных карт приведены в табл.