Индукция и дедукция как методы познания

 

Вопрос об использовании индукции и дедукции в качестве методов познания обсуждался на протяжении всей истории философии. Под индукцией чаще всего понималось движение познания от фактов к утверждениям общего характера, а под дедукцией — движение мысли от общих утверждений к менее общим, в том числе к утверждениям об отдельных предметах. Часто эти методы противопоставлялись друг другу и рассматривались в отрыве от других средств познания. Так, Ф.Бэкон считал основным методом познания индукцию, а Р. Декарт — дедукцию вместе с интуицией. Однако в эпоху Нового времени эти крайние точки зрения начали преодолеваться. Так, Г.Галилей, И.Ньютон, Г.Лейбниц, признавая за опытом, а значит, и за индукцией большую роль в познании, отмечали вместе с тем, что процесс движения от фактов к законам не является чисто логическим процессом, а включает в себя интуицию. Они отводили важную роль дедукции при построении и проверке научных теорий и отмечали, что в научном познании важное место занимает гипотеза, не сводимая к индукции и дедукции. Однако полностью преодолеть противопоставление индуктивного и дедуктивного методов познания долгое время не удавалось.

В современном научном познании противопоставление индукции и дедукции как методов познания теряет смысл, поскольку они не рассматриваются как единственные методы. В познании важную роль играют другие методы, а также приемы, принципы и формы (например, абстрагирование, идеализация, проблема, гипотеза и т.д.).

Контрольные вопросы

 

1. Что представляют собой индуктивные умозаключения? 2. В чем отличие отношения подтверждения от отношения логического (дедуктивного) следования? 3. Что собой представляет обратная дедукция? 4. Каковы методологические требования, выполнение которых повышает степень правдоподобия заключения, получаемого посредством обратной дедукции? 5. В чем различие между абсолютной и статистической неполной индукцией? 6. Какие методологические требования необходимо соблюдать при индукции через отбор? 7. На какой методологии основаны методы установления причинных связей между явлениями? 8. В чем специфика применения методов установления причинной связи в социальном познании? 9. Каковы основные виды умозаключений по аналогии? 10. Каковы основные функции аналогии?

 

ГЛАВА VI

ПОНЯТИЕ

ПОНЯТИЕ КАК МЫСЛЬ ОСОБОГО ВИДА. ЛОГИЧЕСКАЯ ФОРМА ПОНЯТИЯ

 

Важнейшими видами мыслей, в которых отражается действительность в процессе абстрактного мышления, являются понятия. По этой причине абстрактное мышление называют также понятийным мышлением.

В логике исследуются понятия как мысли особого вида, способы выявления логических форм понятий и установления отношений между понятиями и т.д.

В понятиях на основе определенных признаков выделяются предметы классов. Когда мы можем сказать, что человек имеет понятие о предметах какого-либо класса? В том случае, если этот человек может указать систему признаков, общую для предметов данного класса и в то же время не принадлежащую предметам, которые не входят в этот класс.

Примеры понятий:

 

А: общественно опасное действие или бездействие, квалифицируемое законом в качестве уголовно наказуемого.

В: плоская замкнутая прямоугольная геометрическая фигура с равными сторонами.

 

П о н я т и е — это мысль, в которой обобщены в класс и выделены из некоторого множества предметы по системе признаков, общей для этих выделенных предметов и отличающей их от других предметов исходного множества. Слово “предмет” употребляется здесь в самом широком смысле. Предметом называется то, что может быть мыслимо.

Множество, из которого выделяется класс предметов, обобщаемых в понятии, называется родом понятия, или универсумом рассуждения.

Областью, из которой выделяется класс преступлений (родом этого понятия), является класс общественно опасных деяний. Областью, из которой выделяются квадраты, является класс геометрических фигур.

Выделяемыми и обобщающими предметами могут быть не только отдельные объекты, но и совокупности или упорядоченные множества объектов.

Пример понятия о совокупностях объектов: дети, одновременно рожденные одной матерью. Пример понятия об упорядоченных множествах объектов: пара чисел таких, что первое число больше второго.

Языковой формой выражения понятий являются общие описательные имена. Неописательные имена не всегда выражают понятия, а лишь в тех случаях, когда они введены в качестве сокращений для общих описательных имен. Поэтому неописательные имена можно считать знаками понятий лишь в тех случаях, когда известно, что они имеют приданный смысл, являющийся понятием, и известно, какой это смысл. Иначе может произойти подмена понятий именами, не выражающими таковых. Особенно неприемлемо это в процессе обучения.

При определении понятия не говорилось о том, по каким признакам происходит обобщение и выделение предметов в понятии — по существенным или несущественным. Часто важно иметь не любое понятие о предметах, а научное, т.е. такое, в котором предметы обобщаются и выделяются по системе существенных признаков.

Упражнение 1

 

Сравните определение понятия, данное в этом параграфе, со следующими определениями.

1. “Понятие — это мысль, посредством которой в суждении отражается предмет суждения, его свойства, а также отношения между предметами.” (Логика. М., 1956)

2. “Понятие — это высшая форма мысли, в которой отображается сущность предмета или класса предметов.” (Кондаков Н.И. Логика. М., 1954)

3. “Понятие есть мысленное отражение в форме непосредственного единства общих существенных признаков предметов.” (Формальная логика. Л., 1977)

4. “Понятие — это форма мышления, в которой отражаются существенные и отличительные признаки отдельного предмета или класса однородных предметов.” (Гетманова А.Д. Логика. М., 1986)

5. “Понятие — это форма мышления, отражающая предметы в их существенных признаках.” (Кириллов В.И., Старченко А.А. Логика. М., 1987)

Упражнение 2

 

Охарактеризуйте следующие понятия.

1. Тайное похищение государственного имущества.

2. Реальность, познаваемая человеком и существующая независимо от познания.

3. Число, которое делится на 2 или на 3, но не делится на 6.

4. Пара натуральных чисел, таких, что первое число больше второго.

5. Человек, знающий некоторые современные европейские языки и не знающий ни одного древнего языка.

6. Лица, совместно совершившие данное преступление.

ПРИЗНАКИ ПРЕДМЕТОВ И ИХ ВИДЫ

 

Поскольку в понятиях предметы обобщаются и выделяются на основе систем признаков, целесообразно познакомиться с основными видами признаков.

Признак — это наличие или отсутствие свойства у предмета, а также наличие или отсутствие отношения между предметами.

По типам логических форм признаки делятся на простые и сложные, а также на положительные и отрицательные.

Простым является признак, выражаемый в языке словом или словосочетанием, не содержащим логических терминов, кроме, может быть, кванторных слов и одного знака отрицания. Признак, не удовлетворяющий этим условиям, является сложным.

Примеры простых признаков:

быть столицей Франции;

не быть столицей Франции;

быть столицей какого-то государства.

Признак “делиться на 2 и на 3 ” — сложный.

На положительные и отрицательные будем делить только простые признаки. Простыми положительными признаками назовем те, которые не содержат отрицания, а отрицательными назовем признаки, содержащие отрицание. Признак “не есть столица России” — отрицательный, а “есть столица России” — положительный. В языке отрицательные признаки выражаются не только при помощи связки “не есть (суть)”, но и с помощью приставок “без-“, “бес-“ (бездарный, бесформенный, бесталанный) и т.д.

Разделить сложные признаки на положительные и отрицательные по отсутствию или наличию отрицания в словосочетании, выражающем этот признак, не удается.

Упражнение 3

 

Охарактеризуйте следующие признаки.

1. “Быть участником и организатором данного преступления”.

2. “Быть учащимся, но не быть студентом”.

3. “Иметь общую границу”.

4. “Относиться к сообществу живых существ, способному производить орудия труда”.

5. “Быть городом, являющимся столицей России.”

 

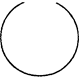
СОДЕРЖАНИЕ И ОБЪЕМ ПОНЯТИЯ

Содержание понятия — это система признаков, на основе которой осуществлено обобщение и выделение предметов в понятии.

Например, содержание понятия “число, которое делится на 2 или на 3” — “делиться на 2 или на 3”.

Различают логическое и фактическое содержание понятия.

Логическое содержание — это та информация, которую несет логическая форма понятия. Чтобы выявить логическое содержание понятия, надо отвлечься от смыслов и значений дескриптивных терминов, входящих в словосочетание, выражающее понятие.

Что дает знание логического содержания понятия? Во-первых, по логическому содержанию можно установить, является ли понятие универсальным, т.е. выделен ли в нем весь универсум рассуждения (род). Во-вторых, по логическому содержанию можно установить, является ли понятие пустым в том смысле, что в нем не выделяется ни один предмет из универсума. В-третьих, логические содержания могут использоваться при установлении отношений между понятиями.

Примеры универсального и пустого понятий: “человек, знающий некоторые европейские языки, или не знающий ни одного европейского языка”, “ студент, сдавший все экзамены и не сдавший экзамен по уголовному праву”.

Фактическое содержание понятия делится на основное и полное. Основное фактическое содержание — это система признаков, на основе которой осуществлено обобщение и выделение предметов в понятии, рассматриваемая сама по себе, т.е. без учета всего имеющегося знания об обобщаемых предметах, о связях признаков, входящих в эту систему, с другими признаками и т.д.

Полное фактическое содержание — это содержание понятия с учетом всего имеющегося знания о предметах, обобщаемых в понятии, о признаках, по которым происходит обобщение, и т.д.

Очевидно, что основное и полное содержания одного и того же понятия могут не совпадать.

Например, основное содержание понятия “химические вещества, имеющие одинаковый состав атомов в молекулах, но различающиеся структурой” (понятие изомеров) выражается предикатом “иметь одинаковый состав атомов в молекулах, но различаться структурой”. В химии известно, что вещества, имеющие различную структуру молекул, обладают различными (по крайней мере, некоторыми) химическими свойствами. Учитывая это знание, следует включить в полное содержание понятия признак “обладать различными химическими свойствами”. В основное содержание рассматриваемого понятия этот признак не включается.

Объем понятия – это множество предметов, обобщаемых и выделяемых в понятии, т.е. множество предметов, которые характеризуются системой признаков, составляющей содержание понятия.

Естественно различать логический и фактический объемы понятия.

Логический объем – это класс предметов, обладающий системой признаков, составляющей логическое содержание понятия.

Фактический объем – это класс предметов, обладающий системой признаков, составляющей фактическое содержание понятия.

Отдельные предметы, относящиеся к классу предметов, представляющему собой объем понятия, называют элементами объема понятия. Элементами объема понятия о человеке являются отдельные люди. Подклассы объема понятия, не совпадающие с ним и не являющиеся пустым множеством, называются частями объема.

Объем понятия можно представить графически в виде круга, заполненного точками. Каждая точка этого круга представляет какой-то один элемент объема понятия. Например, объем понятия о человеке графически можно представить в виде круга А.

Связь между содержанием и объемом понятия выражается в логическом законе обратного отношения между ними, который можно сформулировать так: пусть имеются два понятия, содержание одного из которых меньше содержания второго, тогда объем первого больше объема второго.

Например, сравнивая содержание понятий “преступление” и “хозяйственное преступление”, мы можем утверждать, что содержание первого меньше, чем содержание второго. Объемы же этих понятий находятся в обратном отношении, поскольку хозяйственных преступлений меньше, чем всех преступлений.

В традиционной логике не было точных критериев сравнения понятий по содержаниям. Считалось, что содержание одного понятия больше содержания другого, если содержание первого включает в себя больше признаков, чем содержание другого. В тех случаях, когда признаки объединены союзом “и”, такое понимание может быть приемлемо, но не всегда. Так, содержание понятия “число, которое делится на 2 и 3” больше содержания понятия “число, которое делится на 2”. Если же сравнить понятия “число, которое делится на 2 и 3” и “число, которое делится на 2”, то окажется, что сравнение содержаний по количеству признаков не позволяет установить, какое понятие больше по содержанию.

В традиционной логике не различались логические и фактические содержания, а также логический и фактический объемы. Все это ставило под сомнение правильность закона обратного соотношения. Приводились случаи отношений между объемами и содержаниями понятий, противоречащие закону. Известен следующий пример Больцано: содержание понятия (1) “человек, знающий все живые европейские языки”, по его мнению, больше содержания понятия (2) “человек, знающий все европейские языки”, но и объем первого понятия больше объема второго.

Содержание понятия (1) больше содержания понятия (2), если и только если из первого содержания следует второе, а обратное неверно, то есть если и только если информация, выражаемая содержанием второго, является частью информации, выражаемой содержанием первого понятия, и обратное неверно.

Какое из содержаний “знает все живые европейские языки” и “знает все европейские языки” информативнее? Из того, что человек знает все европейские языки, следует что он знает все живые европейские языки, обратное же не имеет места. Следовательно, содержание понятия (2) примера Больцано больше содержания понятия (1). Объемы же этих понятий находятся в обратном отношении. Таким образом, проблема, сформулированная Больцано, легко разрешима.

Пример, подтверждающий необходимость различать фактическое и логическое содержания, а также фактический и логический объемы. Пусть даны понятия (1) “живое существо, обладающее членораздельной речью”; (2) “живое существо, обладающее абстрактным мышлением и членораздельной речью”. Логическое содержание второго из них больше логического содержания первого, так как из наличия у предметов двух признаков следует наличие одного из них. Очевидно, что объемы этих понятий одинаковы. Как быть? Нужно различать указанные выше объемы содержаний и объемов. Здесь сопоставлялись логические содержания понятий (1) и (2), и их фактические объемы. Очевидно, что, используя наши знания о соотношении признаков человека, т.е. сопоставляя фактические (полные) содержания, мы обнаружим, что эти содержания равны.

 

Упражнение 4

 

Укажите фактические и логические объемы и содержания следующих понятий.

1. “Город с населением более миллиона человек”.

2. “Город России с населением более миллиона человек”.

3. “Самый большой город России”.

4. “Разумное животное”.

5. “Разумное животное, обладающее членораздельной речью”.

6. “Наука о мышлении”.

7. “Наука об обществе”.

Упражнение 5

 

Проанализируйте следующее рассуждение, используя полученные знания об объеме и содержании понятия.

«Больцано пытался критиковать закон обратного отношения между объемом и содержанием понятия традиционной логики, но безуспешно. В доказательство несостоятельности этого закона он приводил, в частности, следующий пример: объемы понятий “круглый шар” и “шар” одинаковы, но содержание первого больше содержания второго. Но этот пример не может поколебать закон обратного отношения между объемом и содержанием понятия. Дело в том, что шар — это геометрическое тело, получающееся при вращении круга вокруг своего диаметра, поэтому каждый шар — это круглый шар и, следовательно, содержание понятий “круглый шар” и “шар” одинаково.» (Кондаков Н.И. Логический словарь-справочник. М., 1975. С. 71)

ВИДЫ ПОНЯТИЙ

 

Понятия делятся на виды по: (1) количественным характеристикам объемов понятий; (2) типу обобщаемых предметов; (3) характеру признаков, на основе которых обобщаются и выделяются предметы. Большей частью эта классификация относится к простым понятиям (понятиям, содержаниями которых являются простые признаки).

По количеству обобщаемых предметов понятия делятся на понятия с пустым (нулевым) объемом и понятия с непустым (ненулевым) объемом.

Пустым по объему называется понятие, в объеме которого нет ни одного предмета из универсума рассуждения. Содержаниями таких понятий являются системы признаков, не принадлежащие ни одному предмету из универсума. Примеры: (1) “вечный двигатель”; (2) “вещество, являющееся металлом и не являющееся электропроводным”; (3) “человек, знающий все европейские языки, но не знающий болгарского языка, являющегося европейским”.

Пустота приведенных понятий обусловлена разными обстоятельствами. Первые два пусты из-за противоречивости их фактических содержаний[21], т.е. из-за противоречивости содержаний в рамках имеющегося знания. Содержание первого противоречиво в силу закона сохранения энергии. Содержание второго — в контексте со знанием “все металлы электропроводны”.

Первые два понятия имеют пустой фактический объем. Логические же объемы этих понятий не пусты. Содержание третьего из приведенных выше понятий самопротиворечиво (логически противоречиво). Оно имеет пустой логический объем.

Возникновение понятий, логическое содержание которых противоречиво, связано с ошибками в познании. Такие ошибки иногда совершаются при образовании сложных понятий, например, в математике.

Понятия, логические содержания которых непротиворечивы, а фактические противоречивы, возникают в следующих случаях.

Первый. В науке образуют понятия не только о тех предметах, существование которых установлено, но и о тех, существование которых лишь предполагается. При образовании понятий последнего типа проявляется активный характер познания. В результате дальнейших исследований может оказаться, что этим понятиям ничто не соответствует в действительности, и их фактическое содержание противоречиво. Такими понятиями являются понятия теплорода, мирового эфира, живых существ, обитающих на Марсе. В момент образования таких понятий их фактическое содержание противоречивым не является. Оно становится таковым с развитием знания.

Второй. В науке образуются понятия, содержание которых с самого момента их образования является противоречивым в контексте всего имеющегося знания. Предметы, обобщаемые в этих понятиях, не существуют в действительности. Примеры таких понятий: “идеальный газ”, “абсолютно черное тело”. Понятия этого вида необходимы при построении теорий. В рамках этих теорий (в рамках универсума рассуждении) их содержания не являются противоречивыми.

Среди понятий с непустым объемом выделяют единичные и общие. В объеме единичного понятия содержится один элемент, а в объеме общего более одного элемента. Общие делятся на универсальные и неуниверсальные. Объемом универсального понятия является весь универсум, а объемом неуниверсального — не весь.

По типу обобщаемых предметов понятия делятся на собирательные и несобирательные, а также на конкретные и абстрактные.

Элементами объемов собирательных понятий являются совокупности однородных предметов, мыслимые как целое, т.е. как некие агрегаты. Примеры собирательных понятий: “народ”, “студенческая группа”. В этих понятиях соответственно обобщаются народы и группы. Указанные понятия являются общими. Собирательные понятия могут быть единичными. Пример: “российский народ”.

Элементами несобиратсльных понятий являются отдельные предметы. Примеры: “планета Солнечной системы”, “Московский государственный университет”.

Конкретными называются понятия, в которых обобщены сами предметы, существующие в универсуме рассуждения. Абстрактными — те, в которых обобщены отдельные стороны, свойства, отношения предметов, существующих в универсуме рассуждения. Если универсумом рассуждения является множество тел, то “твердость” — пример абстрактного понятия.

По характеру признаков, на основе которых обобщаются и выделяются предметы, понятия делятся на положительные и отрицательные, а также на относительные и безотносительные.

Охарактеризуем простые положительные и отрицательные понятия.

Содержанием положительного понятия является положительный признак, а отрицательного — отрицательный. Примеры положительных понятий: “живущий по средствам”, “говорящий по-английски”. Примеры отрицательных понятий: “живущий не по средствам”, “не говорящий по-английски”.

Как применить это деление к сложным понятиям? Общего метода мы дать не можем.

Пример сложного положительного понятия: “человек, знающий английский, немецкий и французский языки”. Пример сложного отрицательного понятия: “человек, знающий английский и не знающий немецкого или французского языка”.

Как и в предшествующем случае, дадим сначала характеристику простых относительных и безотносительных понятий.

Относительным является понятие, содержание которого представляет собой наличие или отсутствие отношения выделяемых предметов к некоторым другим предметам. Примеры: “мать”, “отец”.

Понятия, в одном из которых предметы выделены на основе их отношения к другим предметам, а в другом — на основе отношения к первым, называются соотносительными. Пример: “причина”, “следствие”.

В безотносительных понятиях предметы выделяются на основе наличия или отсутствия у них характеристик самих предметов, не указывающих на отношения предметов к другим предметам.

Сложное понятие является относительным, если среди конъюнкции признаков, составляющих его содержание, есть простые признаки, представляющие собой наличие или отсутствие отношений. Пример сложного относительного понятия: “человек, имеющий высшее образование и не знающий русского языка”.

Рассмотренное в этом параграфе деление на виды понятий о предметах можно распространить и на понятия о системах предметов.

Упражнение 6

 

К какому виду относится каждое из следующих понятий?

1. “Самая удаленная точка Вселенной”.

2. “Значимая часть слова” (“Морфема”).

3. “Человек, который никого не любит”.

4. “Записка или письмо с просьбой куда-нибудь явиться” (“Письменное приглашение”).

5. “Призрак умершего или отсутствующего существа” (“Привидение”).

6. “Человек, у которого отсутствует воля” (“Безвольный человек”).

7. “Человек, не знающий страха”.

8. “Отсутствие страха перед опасностью”.

9. “Бестелесная простая единица бытия, являющаяся неделимой, неуничтожимой, неповторимой, психически активной и т.д.” (“Монада Лейбница”).

10. “Разумное существо, живущее на Марсе”.

11. “Натуральное число, которое больше каждого двухзначного простого числа, но не больше 13, являющегося простым”.

12. “Необезвреженные сточные воды”.

13. “Не имеющий надлежащего гуманитарного образования”.

14. “Моя третья первая любовь”.

15. “Первый заместитель главы правительства Российской Федерации”.

16. “Не имеющий надлежащего юридического образования”.

17. “Преступление”.

18. “Человек, который ничего не знал о данном факте, но собственноручно написал о нем другому”.

19. “Человек, который застрелился, нанеся себе три раны, каждая из которых вызвала немедленную смерть”.

 

ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ

 

При образовании понятий часто бывает важно не только указывать их вид, но и выяснять, в каком отношении находятся эти понятия к другим понятиям. Высказывания типа “это понятие близко такому-то понятию” только запутывают суть дела. Нужно точно указать вид отношения данного понятия к другим понятиям. Сделать это помогает логика.

Между понятиями, имеющими общий род, можно устанавливать отношения по содержаниям. Последним соответствуют определенные отношения по объемам, кроме случая, когда понятия находятся в отношении независимости по содержаниям (это отношение описывается ниже).Отношениям между понятиями по объемам не всегда соответствуют определенные отношения по содержаниям.

По содержаниям между понятиями существуют отношения, аналогичные отношениям между высказываниями. Сначала рассмотрим отношения по логическим содержаниям. Пусть даны два понятия: (1) и (2). Понятие (1) шире понятия (2) по содержанию (содержание понятия (1) больше содержания понятия (2)), если и только если из первого содержания следует второе, а обратное не имеет места. Если понятие (1) шире понятия (2) по содержанию, то в силу закона обратного отношения объем понятия (1) меньше объема понятия (2).

Понятия (1) и (2) эквивалентны по содержаниям, если и только если из содержания первого понятия следует содержание второго, а из содержания второго — содержание первого. Объемы таких понятий равны. Например, “человек такой, что если он студент, то он отличник” и “человек такой, что он не студент или отличник”.

Понятия (1) и (2) находятся в отношении противоречия (контра-дикторности) по содержаниям, если и только если их содержания несовместимы по истинности и несовместимы по ложности. Пример: “студент, который сдал все экзамены”, “студент, который не сдал некоторых экзаменов”. Объемы этих понятий не имеют общих элементов и исчерпывают весь универсум. Графически:

 

 

Понятия (1) и (2) находятся в отношении контрарности по содержаниям, если и только если их содержания несовместимы по истинности, но совместимы по ложности. Пример: “студент, который сдал все экзамены на отлично”, “студент, который не сдал ни одного экзамена на отлично”.

 

Графически это отношение может быть представлено схемой:

 

 

Понятия (1) и (2) находятся в отношении субконтрарности по содержаниям, если и только если их содержания совместимы по истинности, но несовместимы по ложности. Пример: “студент, сдавший некоторые экзамены на отлично” и “студент, не сдавший некоторых экзаменов на отлично”. Графически:

 

 

Понятия (1) и (2) находятся в отношении логической независимости по содержаниям, если и только если их содержания логически независимы, то есть совместимы по истинности и ложности и между ними нет отношения логического следования. Пример: “человек, который побывал в Москве”, “человек, который побывал в Архангельске”. Отношение по объемам между этими понятиями не определено.

Указанные отношения имеют место между логическими содержаниями понятий. Аналогичные отношения можно устанавливать между фактическими содержаниями.

Поскольку определенным отношениям между понятиями по объемам не всегда соответствуют определенные отношения по содержаниям, рассмотрим особо отношения между понятиями по объемам.

По характеру отношений между объемами понятия делятся на совместимые и несовместимые.

Совместимыми называются понятия, объемы которых полностью или частично совпадают. Совместимыми являются понятия “слушатель” и “спортсмен”, “юрист” и “следователь” и т.д. Несовместимыми называются понятия, не имеющие общих элементов объемов. Понятия “собственник" и “неимущий” являются несовместимыми.

Совместимые понятия могут находиться в отношениях:

1) равнозначности; 2) подчинения и 3) перекрещивания.

Охарактеризуем виды отношений между совместимыми понятиями.

В отношении равнозначности находятся понятия, объемы которых полностью совпадают. Например, понятия “живое существо, имеющее мягкие мочки ушей” и “живое существо, обладающее членораздельной речью”, находятся в отношении равнозначности.

Если объем первого из них представить графически в виде круга А, а второго — в виде круга В, то отношение между этими понятиями по объемам будет представлено схемой:

 

а. в.

 

В отношении подчинения находятся понятия, объем одного из которых полностью входит в объем другого, но обратное не имеет места. В этом отношении находятся понятия “юрист” (А) и “адвокат” (В). Графически это отношение представляется так:

 

 

Понятие большого объема, в данном случае “юрист”, называется подчиняющим, а понятие меньшего объема, в данном случае “адвокат”, называется подчиненным.

В отношении перекрещивания находятся понятия, объем одного из которых частично входит в объем другого, а объем другого частично входит в объем первого. В отношении перекрещивания находятся, например, понятия “слушатель” (А) и “спортсмен” (В). Графически это отношение изображается так:

 

 

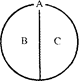
Особым видом отношения между понятиями является отношение соподчинения.

В отношении соподчинения к некоторому понятию находятся два несовместимых понятия, каждое из которых является подчиненным по отношению к этому третьему понятию. Иными словами, два понятия находятся в отношении соподчинения к третьему понятию, если они не имеют общих элементов объемов и это третье понятие является подчиняющим для каждого из них. Например, понятия “получение взятки” (В), “незаконное изготовление спиртных напитков” (С) находятся в отношении соподчинения к понятию “преступление” (А). Отношение соподчинения представляется следующими круговыми схемами:

 

Если отношение между объемами понятий представляется первой из этих схем, то это еще не означает, что понятия находятся в отношении противоречия по логическим или фактическим содержаниям.

Устанавливая отношения между понятиями, важно не отождествлять понятия с общими именами или просто словами, не выражающими понятий. Чтобы избежать такого отождествления, нужно всякий раз выяснять, какие понятия выражают те или иные слова или словосочетания. Пусть, например, требуется установить, в каких отношениях по объемам находятся понятия (1) “стоимость”, (2) “потребительная стоимость”, (3) “меновая стоимость”. На первый взгляд кажется, что объем понятия (1) включает в себя объемы понятий (2) и (3), а понятия (2) и (3) являются несовместимыми между собой, т.е. что два последних понятия находятся в отношении соподчинения к первому. Так ли это на самом деле?

Выявим понятия, вместо которых введены слова “стоимость”, “потребительная стоимость”, “меновая стоимость”. Эти понятия следующие: (1) “Определенное количество общественно необходимого труда, затраченное на производство товара”; (2) “Полезность вещи, ее способность удовлетворять какую-либо человеческую потребность”; (3) “Количественное соотношение, в котором обмениваются товары как потребительные стоимости”.

Эти понятия несовместимы по объемам. Первое понятие — один из видов стоимости наряду с потребительной и меновой. С логической точки зрения для этого (первого) понятия нужно ввести другое название — какая-то специфическая стоимость — и образовать новое понятие, в объем которого войдут объемы всех трех рассмотренных понятий. Сокращением для словесного выражения понятия (4) целесообразно использовать слово “стоимость”.

Упражнение 7

 

Установите, в каких отношениях попарно находятся следующие понятия? Изобразите отношения между их объемами посредством круговых схем.

1. “Деяние”. “Наказуемое деяние”. “Ненаказуемое деяние”.

2. “Предмет, имеющий какой-либо цвет”. “Белый предмет”. “Черный предмет”.

3. “Треугольник”. “Прямоугольный треугольник”. “Непрямоугольный треугольник”.

4. “Орудие преступления”. “Огнестрельное оружие”. “Пистолет”.

5. “Преступление против личности”. “Преступление против жизни”. “Преступление против здоровья”.

6. “Посягательство на честь и достоинство личности”. “Клевета”. “Оскорбление”.

7. “Хозяйственное преступление”. “Обман покупателей”. “Незаконное изготовление спиртных напитков”.

8. “Человек, изучивший все восточные языки”. “Человек, не изучивший японского языка”. “Человек, не изучивший некоторых восточных языков”.

9. “Гражданин России”. “Российский военнослужащий”.

10. “Преступление”. “Терроризм”. “Спекуляция”.

11. “Действие или бездействие, квалифицируемое законом в качестве уголовно наказуемого”. “Действие, квалифицируемое законом в качестве уголовно наказуемого, или бездействие, квалифицируемое законом в качестве уголовно наказуемого”.