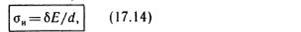Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цель курса «Детали машин». Механизм и машина. Детали и сборочные единицы машин, их основные характеристики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель курса «Детали машин». Механизм и машина. Детали и сборочные единицы машин, их основные характеристики. Детали машин — техническая дисциплина, в которой изучают методы, правила и нормы расчета и конструирования типовых деталей машин и сборочных единиц. Целью является изучения основ расчета и конструирования деталей и узлов общего назначения с учетом режима работы и срока службы машины. При этом рассмотрим выбор материала, его термообработка, рациональные формы деталей, их технологичность и точность изготовления. Изделие изготовленное из однородного материала без применения сборочных и монтажных операций называется деталью. Изделия состоящее из нескольких деталей соединенных между собой сборочными операциями называется сборочными единицами. В машиностроении различают детали и узлы общего и специального назначения. Общего назначения: болты, гайки, валы, зубчатые колеса. Специального назначения: применяются в некоторых машинах (шпиндели).
Современные направления в развитии машиностроения. Основные задачи научно-технического прогресса. Современное машиностроение базируется на наукоемких технологиях. Таким образом, в конце XX столетия была продемонстрирована зависимость машиностроительных производств не только от развития энергетики, но в значительной мере и от развития наукоемких технологий. Появление таких продуктов электронного машиностроения, как современные электронные компьютерные компоненты, привело к широкому их внедрению в производство нового поколения технических систем, высокоэффективных, гибко перестраиваемых, многокоординатных машин и роботов. Ключевой тенденцией при создании современных машин стал перенос функциональной нагрузки с механических узлов к интеллектуальным (электронным, компьютерным) компонентам. Информатизация и компьютеризация производства сопровождаются информатизацией общества, всех сторон его жизни и трудовой деятельности на базе телекоммуникации и информационных компьютерных сетей (Интернет), факсимильных аппаратов, почты, сотовой и космической связи. Приоритетными сегодня считаются такие направления, как электронная, автомобильная и авиационная отрасли, что объясняется высокой стоимостью производимой ими продукции. К тому же спрос на такую продукцию всегда высок, равно, как и на услуги по ее обслуживанию. В постиндустриальном обществе любая техника или оборудование должны удовлетворять в первую очередь интересы и потребности каждого индивида.
Требования к конструкции деталей и сборочных единиц. Понятие работоспособности, технологичности, экономичности. Критерии работоспособности. Работоспособность — состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения заданных параметров в пределах установленных нормативно-технической документации. Основные критерии работоспособности: прочность, жесткость, устойчивость, теплостойкость, виброустойчивость. Прочность — свойство материала сопротивляется нагрузкам без разрушения. Наиболее распространен метод оценки прочности деталей это сравнения расчетных (рабочих) напряжений, возникающих в опасном сечении при действии эксплуатационных нагрузок с допускаемыми напряжениями.
Сравнение действительного коэффициента запаса прочности рассчитываются детали с допускаемым коэффициента запаса прочности. Жесткость - способность детали сопротивляться изменению формы и размеров под нагрузкой. Устойчивость, критерий работоспособность длинных стержней, а так же пластин подвергающих сжатию, силами лежащими в их плоскости, а также оболочек испытывающим внешнее давление либо осевое сжатие. Износостойкость - свойство оказывающее сопротивление изнашиванию в определенных условиях трения. Виброустойчивость - способность конструкций работать в нужном диапазоне режимов, исключающих резонанс. Теплостойкость - способность конструкций работать в пределах заданных температур в течении заданного срока службы. Технологичными называют детали и узлы требующие минимальных затрат, средств, времени и труда в производстве, эксплуатации и ремонте.
Способы изготовления лезвийная обработка резанием; абразивная обработка; накатывание; выдавливание прессованием; литьё; электрофизическая и электрохимическая обработка. Наиболее распространённым и универсальным способом получения резьб является лезвийная обработка резанием. К ней относятся:нарезание наружных резьб плашками; нарезание внутренних резьб метчиками; точение наружных внутренних резьб резьбовыми резцами и гребёнками; резьбофрезерование наружных и внутренних резьб дисковыми и червячными фрезами; нарезание наружных и внутренних резьб резьбонарезными головками; вихревая обработка наружных и внутренних резьб. Накатывание является наиболее высокопроизводительным способом обработки резьб, обеспечивающим высокое качество получаемой резьбы. К накатыванию резьб относятся: накатывание наружных резьб двумя или тремя роликами с радиальной, осевой или тангенциальной подачей; накатывание наружных и внутренних резьб резьбонакатными головками; накатывание наружных резьб плоскими плашками; накатывание наружных резьб инструментом ролик-сегмент; накатывание (выдавливание) внутренних резьб бесстружечными метчиками. К абразивной обработке резьб относится шлифование однониточными и многониточными кругами. Применяется для получения точных, в основном ходовых резьб. Выдавливание прессованием применяется для получения резьб из пластмасс и цветных сплавов. Не нашло широкого применения в промышленности. Литьё (обычно под давлением) применяется для получения резьб невысокой точности из пластмасс и цветных сплавов. Электрофизическая и электрохимическая обработка (например, электроэрозионная, электрогидравлическая) применяется для получения резьб на деталях из материалов с высокой твердостью и хрупких материалов, например твёрдых сплавов, керамики и т. п. Заклёпочные соединения
Достоинства заклёпочного соединения: + соединяют не свариваемые детали ( Al ); + не дают температурных деформаций; + детали при разборке не разрушаются. Недостатки заклёпочного соединения: ` детали ослаблены отверстиями; ` высокий шум и ударные нагрузки при изготовлении; ` Заклёпки изготавливают из сравнительно мягких материалов: Ст2, Ст3, Ст10, Ст15, латунь, медь, алюминий.
26-27.
Заклёпки испытывают сдвиг (срез) и смятие боковых поверхностей. По этим двум критериям рассчитывается диаметр назначаемой заклёпки. При этом расчёт на срез – проектировочный, а расчёт на смятие – проверочный. Здесь и далее имеем в виду силу, приходящуюся на одну заклёпку.
Напряжения смятия на боковых поверхностях заклёпки s см = P/Sd ≤ [ s ] см, где S – толщина наименьшей из соединяемых деталей. При проектировании заклёпочных швов как, например, в цистернах, необходимо следить, чтобы равнодействующая нагрузок приходилась на центр тяжести шва. Следует симметрично располагать плоскости среза относительно линии действия сил, чтобы избежать отрыва головок. Кроме того, необходимо проверять прочность деталей в сечении, ослабленном отверстиями.
Шпоночные соединения
Шпоночные соединения: + просты, надёжны; + удобны в сборке-разборке; + дёшевы. Шпонки, однако: ` ослабляют сечение валов и ступиц колёс; ` концентрируют напряжения в углах пазов; ` нарушают центрирование колеса на валу (для этого приходится применять две противоположные шпонки). Шпоночные соединения могут быть: -ненапряжёнными, выполняемыми призматическими или сегментными шпонками. Они передают момент только боковыми гранями; -напряжёнными, выполняемыми клиновыми шпонками. Шлицевые соединения
В основном используются прямобочные шлицы (а), реже встречаются эвольвентные (б) ГОСТ 6033-57 и треугольные (в) профили шлицов. Прямобочные шлицы могут центрировать колесо по боковым поверхностям (а), по наружным поверхностям (б), по внутренним поверхностям (в). В сравнении со шпонками шлицы: + имеют большую несущую способность; + лучше центрируют колесо на валу; + усиливают сечение вала за счёт большего момента инерции ребристого сечения по сравнению с круглым; ` требуют специального оборудования для изготовления отверстий.
Основными критериями работоспособности шлицов являются: è сопротивление боковых поверхностей смятию (расчёт аналогичен шпонкам); è сопротивление износу при фреттинг-коррозии (малые взаимные вибрационные перемещения). Силы в зацеплении Силы принято определять в полюсе W (рис.5) зацепления.
По линии зацепления b – b (рис. 5) действует нормальная сила Fn. Для удобства расчетов силу Fn принято раскладывать на три составляющие: 1) Ft – окружная сила, направленная по касательной к делительным окружностям. Это основная, движущая, полезная сила. На колесе z2 Ft совпадает с направлением вращения n2. На шестерне z1 F направлена против вращения n1. Следовательно, на рис. 5 дана схема сил для шестерни: Ft = 2000Т / d, (1) где Т – Н∙м; d – мм; 2) Fr – радиальная сила, направленная по линии центров (радиусам). Для внешнего зацепления – к оси вращения, для внутреннего – от оси. В торцовой плоскости t – t (рис. 5) имеем Fr = tgбt, (2) где бt – делительный угол профиля в торцовой плоскости: tgбt = tgбn / cosв; бn– нормальный угол зацепления, в – угол наклона зубьев. В практических расчетах бt ≈ бn =20°. 3) Fa – осевая сила, направленная параллельно оси а – а зубчатого коле- са. Силы Ft и Fа как составляющие нормальной силы Fn′, всегда находятся вне линии зуба (рис. 5). В делительной плоскости: Fа = Fttgв. (3) Необходимый в дальнейших расчетах основной угол наклона зуба вb (в основной плоскости зацепления b) определяется как вb = arcsin(sinвcosбn). Полная нормальная сила (рис. 5): Fn = Fnt / cosвb = Ft / (cosбtcosвb). (4) Для прямозубых передач во всех формулах в = вb = 0; бt = бn = б; Ft = 2000T / d; Fr = Fttgб; Fa = 0; Fn = Ft / cosб. Недостатком косозубых передач является наличие осевых сил Fа, которые дополнительно нагружают опоры валов, усложняя их конструкцию.
В косозубых передачах углы в ограничены в пределах 8…18°. Указанный недостаток устранен в шевронной передаче, которая представляет собой сдвоенную косозубую с противоположным наклоном зубьев на полушевронах. Из рис. 6 видно, что осевые силы Fа /2 взаимоуравновешены. 42. Геометрические параметры. У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол в (рис. 8.23, где а — косозубая передача; б— шевронная, и рис. 8.24).
Оси колес при этом остаются параллельными. Для нарезания косых зубьев используют инструмент такого же исходного контура, как и для нарезания прямых. Поэтому профиль косого зуба в нормальном сечении з — з совпадает с профилем прямого зуба. Модуль в этом сечении должен быть также стандартным. В торцовом сечении t — t параметры косого зуба изменяются в зависимости от угла в: окружной шаг pt=pn/cos в, окружной модуль mt = mn/cos в, делительный диаметр d=mtz = mnz/cos в. Индексы з и t приписывают параметрам в нормальном и торцовом сечениях соответственно. Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса (рис. 8.25).
Нормальное к зубу сечение образует эллипс с полуосями с —г и e — r\cos в, где r = d/2. В зацеплении участвуют зубья, расположенные на малой оси эллипса, так как второе колесо находится на расстоянии c = d/2. Радиус кривизны эллипса на малой оси (см. геометрию эллипса) rv = e2/с = г/cos2 в.
43. Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под некоторым углом £ (рис. 8.29 и 8.30). Наиболее распространены передачи с углом £ = 90°.
Конические передачи сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических колес требуются специальные станки и специальный инструмент. Кроме допусков на размеры зубьев здесь необходимо выдерживать допуски на углы δ! и δ2, а при монтаже обеспечивать совпадение вершин конусов. Выполнить коническое зацепление с той же степенью точности, Рис. 8.29 что и цилиндрическое, значительно труднее. Пересечение осей валов затрудняет размещение опор. Одно из конических колес, как правило, располагают кон- сольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба (см. рис. 8.13). В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все это приводит к тому, что, по опытны данным, нагрузочная способность конической прямозубой передачи составляет лишь около 0,85 цилиндрической. Несмотря на отмеченные недостатки, конические передачи имеют широкое применение, поскольку по условиям компоновки механизмов иногда необходимо располагать валы под углом. Геометрические параметры. Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами 5t и δ2. При коэффициентах смещения инструмента х1+х2 = 0 начальные и делительные конусы совпадают. Этот наиболее распространенный вариант рассматривается ниже. Конусы, образующие которых перпендикулярны образующим делительных конусов (см. рис. 8.31), называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения. Размеры, относящиеся к внешнему торцовому сечению, сопровождают индексом е, например de, Re и др. Размеры в среднем сечении сопровождают индексом т: dnn Rm и др.; Rc и Rm — внешнее и среднее конусные расстояния, b — ширина зубчатого венца.
Размеры по внешнему горцу удобнее для измерения, их указывают на чертежах. Размеры в среднем сечении используют при силовых расчетах. Зависимости размеров в среднем и торцовом сечениях:
Для прямозубых передач торцовое t и нормальное и сечения совпадают. При этом mte = mne округляют до стандартного (см. табл. 8.1). Силы в зацеплении
1. Окружная сила (рис. 13) Ft = 2000Т / dm. 2. Радиальная сила на шестерне Fr1, равная осевой силе на колесе Fа2: Fr1 = Fа2 = Ft (tgбncosд1 m sinвmsinд1) / cosвm. (13) 3. Осевая сила на шестерне Fа1, равная радиальной силе на колесе Fr2: Fа1 = Fr2 = Ft (tgбnsinд1 ± sinвmcosд1) / cosвm, (14) где в формулах (13) и (14) бn – средний нормальный угол зацепления (бn ≈ 20°); вm = 35° – средний угол наклона зуба; д1 – угол делительного конуса шестерни. Знаки в скобках: если смотреть с вершины делительного конуса О, то при совпадении вращения и наклона зубьев – верхние знаки, при отсутствии совпадения – нижние. Знаки результата: во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление осевой силы Fа1 от вершины к внешнему торцу е1, т.е. сила Fа1 должна быть положительной. Это возможно при совпадении вращения и наклона зубьев. Нормальная сила в зацеплении Fn = Ft / (cosбncosвm). Для прямых зубьев в формулах сил следует положить вm = 0: 1) Ft1 = Ft2 = 2000Т / dm; 2) Fr1 = Fа2 = Fttgб cosд1; 3) Fа1 = Fr2 = Fttgб sinд1; 4) Fn = Ft / cosб. Определение числа зубьев эквивалентного колеса
Для прямозубой передачи профили зубьев конического колеса, построенные на развертке дополнительного конуса, весьма близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса, делительная окружность которого получена разверткой дополнительного конуса на плоскость. Дополнив развертку до полной окружности (рис. 11.5), получим эквивалентное цилиндрическое колесо с числом зубьев жх.
Из треугольника OCS (рис. 11.5) делительный диаметр эквивалентного колеса
Для передачи с круговыми зубьями профили зубьев конического колеса в нормальном сечении близки к профилям зубьев эквивалентного цилиндрического прямозубого колеса с числом зубьев Жы, полученных двойным приведением: конического колеса к цилиндрическому и кругового зуба к прямому зубу [см. формулы (11.3) и (10.5ft]:
В формулах (11.3) и (11.4) ж — действительное число зубьев конических колес.
45. Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же, как и у эквивалентного цилиндрического (см. рис. 11.3), с той же длиной зуба b и профилем, соответствующим среднему дополнительному конусу (среднему сечению зубьев). Однако практика эксплуатации показала, что при одинаковой степени нагруженности конические передачи выходят из строя быстрее цилиндрических. Проверочный расчет. Формула (9.9) в параметрах эквивалентной цилиндрической прямозубой передачи по среднему дополнительному конусу (см. рис. 11.3) имеет вид
Согласно формулам (11.1) и (11.2) Uv = dv2/dv\ = d2 cos дй/(d\ cos д2) = = и sin 62/cos д2 = и2. По формуле (11.2) и табл. 11.2 dv2 = d2/cos d2 = d2 д/tg2 д2+ 1 =d2 -\Ju2+ 1 =0,857^2 ^u2+\. Подставив в формулу (11.10) значения Uv и dv2, получим формулу проверочного расчета для стальных конических зубчатых передачу
где Ft — в З; de2, b — в мм; ыЗ — коэффициент вида конических колес. Для прямозубых колес 0//=0,85. Для колес с круговыми зубьями: 1,85 —при твердости колеса и шестерни Н<350 НВ, 0//=1,5-при твердости колеса Н<350 НВ и шестерни З >45 HRCa, 0//=1,3 — при твердости колеса и шестерни З >45 HRC3; /(яр—коэффициент, учитывающий распределение нагрузки по ширине венца. Для прирабатывающихся колес с прямыми зубьями /С//р= 1» с круговыми зубьями /Сяр= 1,1. Для неприрабатывающихся колес числовое значение Кн$ принимают по табл. 9.1 в зависимости от коэффициента ширины зубчатого венца
Кзь — коэффициент динамической нагрузки. Для передач с прямыми зубьями при й; <5 м/с: = 1,15 при твердости зубьев колеса Н<350 НВ, КЗь=\,\ при твердости зубьев колеса З>350 НВ. Для передач с круговыми зубьями: Khv= 1,05 при'у^Ю м/с и любой твердости зубьев, KHv= 1,2 при t; = 10...20 м/с и твердости зубьев колеса З <350 НВ, при у =10...20 м/с и твердости зубьев колеса З >350 НВ. Проектировочный расчет. Заменив в формуле (11.1) значения F, = 2Т2/ (0,857de2), b = Re = 0,5ш de2 -yfF+l/u и решив относительно de2, запишем, окончательно получим формулу проектировочного расчета для стальных конических зубчатых передач
где de2 — внешний делительный диаметр колеса, мм; Т2— в З•ММ; [у]// — в Н/мм2.
46. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ Червячная передача (рис. 9.1) относится к передачам зацепления с перекрещивающимися осями валов. Угол перекрещивания обычно равен 90°. Возможны и другие углы, отличные от 90, однако такие передачи применяют редко. Движение в червячных передачах преобразуется по принципу винтовой пары или по принципу наклонной плоскости. § 9.1. Геометрические параметры и способы изготовления передач В червячной передаче, так же как и в зубчатой, различают диаметры начальных и делительных цилиндров (рис. 9.2): dwi, dw2 -начальные диаметры червяка и колеса; du d2 - делительные диаметры червяка и колеса. В передачах без смещения dw{=dy, dw2 = d2. Точка касания начальных цилиндров является полюсом зацепления.
Червяки. Различают по следующим признакам: форме поверхнос ги, на которой образуе гея резьба, - - цилиндрические (рис. 9.3,(7) и глобоидные (рис. 9.3,6); форме профиля резьбы- -г прямолинейным (рис. 9.4. а) и криволинейным (рис. 9.4, б) профилем в осевом сечении. Наиболее распространены цилиндрические червяки. У червяков с прямолинейным профилем в осевом сечении в торцовом сечении витки очерчены архимедовой спиралью, отсюда название —архимедов червяк. Архимедов червяк подобен ходовому винту с трапецеидальной резьбой. Его можно нарезать на обычных токарных или резьбофрезерных станках. Поэтому первые червячные передачи выполняли с архимедовыми червяками, которые широко применяют и в настоящее время. Исследования показали, что работоспособность червячной передачи повышается с уменьшением шероховатости поверхности и повышением твердости резьбы червяка (см. ниже). В последнее время все шире стали применять шлифованные высокотвердые червяки при З ^45 HRC. Для шлифования архимедовых червяков требуются специальные шлифовальные круги фасонного профиля, что затрудняет обработку и снижает точность изготовления. Поэтому архимедовы червяки изготовляют в основном с нешлифованными витками при З ^ 350 НВ. Для высокотвердых шлифуемых витков применяют эвольвентные червяки. Эволъвентные червяки имеют эвольвентный профиль в торцовом сечении и, следовательно, подобны косозубым эвольвентным колесам, у которых число зубьев равно числу заходов червяка. Основное преимущество эвольвентных червяков — возможность шлифования витков плоской стороной круга. Однако для этого требуются специальные червячно-шлифовальные станки. Способ изготовления является решающим при выборе профиля нарезки червяка, так как при одинаковом качестве изготовления форма профиля мало влияет на работоспособность передачи. Выбор профиля нарезки червяка связан также с формой инструмента для нарезания червячного колеса. Червячное колесо нарезают червячными фрезами. Червячная фреза для нарезки червячного колеса является копией червяка. Только фреза имеет режущие кромки и наружный диаметр больше на двойной размер радиального зазора в зацеплении. При нарезании заготовка колеса и фреза совершают такое же взаимное движение, какое имеют червячное колесо и червяк в передаче. Такой метод нарезания колеса автоматически обеспечивает сопряженность профилей червяка и червячного колеса и в то же время обусловливает необходимость введения стандарта на основные геометрические параметры червяка для того, чтобы иметь ограниченный ряд стандартного инструмента. КПД червячной передачи КПД червячной передачи, так же как и зубчатой, определяют по формуле (8.51). Различаются только формулы для определения потерь в зацеплении. По аналогии с винтовой парой для червячных передач запишем КПД зацепления при ведущем червяке:
КПД увеличивается с увеличением числа заходов червяка (увеличивается г) и с уменьшением коэффициента трения или угла трения ц. Если ведущим является колесо, то вследствие изменения направления сил получают 9,10.
При г^ц, з, = 0 передача движения в обратном направлении (от колеса к червяку) становится невозможной. Получаем самотормозящую червячную пару. Свойство самоторможения червячных передач используют в грузоподъемных и других механизмах. Следует учитывать, что, согласно формуле (9.9), КПД самотормозящей передачи мал и всегда меньше 0,5. Для надежности самоторможения рекомендуют г^0,5ц. Оценка и применение На основе вышеизложенного можно отменить следующие основные преимущества червячной передачи: возможность получения больших передаточных отношений в одной паре; плавность и бесшумность работы; повышенная кинематическая точность; возможность самоторможения (при низком КПД). Недостатки этой передачи: сравнительно низкий КПД; повышенный износ и склонность к заеданию; необходимость применения для колес дорогих антифрикционных материалов (бронза); повышенные требования к точности сборки (точное aw, совпадение главных плоскостей колеса и червяка). Скольжение Vs=V1/cosb Большое скольжение в червячных передачах служит причиной пониженного кпд, повышенного износа и склонности к заеданию.
47. Основные геометрические соотношения в червячной передаче Геометрические размеры червяка и колеса определяют по формулам, аналогичным формулам для зубчатых колес. В червячной передаче расчетным является осевой модуль червяка т, равный торцовому модулю червячного колеса. Значения расчетных модулей m выбирают из ряда: 2; 2,5; 3,15; 4; 5; 6,3; 8; 10; 12,5; 16; 20 мм. Основными геометрическими размерами червяка являются (рис. 15.6): угол профиля витка в осевом сечении 2а = 40°·
48. Классификация червячных передач В зависимости от формы внешней поверхности червяка (рис. 15.2) передачи бывают с цилиндрическим (а) или с глобоидным (б) червяком. Глобоидная передача имеет повышенный к. п. д., более высокую несущую способность, но сложна в изготовлении и очень чувствительна к осевому смещению червяка, вызванному изнашиванием подшипников. Ниже рассматриваются передачи с цилиндрическими червяками. В зависимости от направления линии витка червяка червячные передачи бывают с правым и левым направлением линии витка. В зависимости от числа витков (заходов резьбы) червяка передачи бывают с одновитковым или м н о г о в и ф к о- в ы м червяком.
В зависимости от расположения червяка относительно колеса (рис. 15.3) передачи бывают с нижним (а), боковым (б) и верхним (в) червяками. Чаще всего расположение червяка диктуется условиями компоновки изделия. Нижний червяк обычно применяют при окружной скорости червяка й>й<5 м/с во избежание потерь на перемешивание и разбрызгивание масла. В зависимости от формы винтовой поверхности резьбы цилиндрического червяка передачи бывают с архимедовым, конволютным и эвольвентным червяками. Каждый из них требует особого способа нарезания. Если резец, имеющий в сечении форму трапеции, установить на станке так, чтобы верхняя плоскость резца А — А проходила через ось червяка (положение 1 на рис. 15.4), то при нарезании получится винтовая поверхность, которая в сечении, перпендикулярном оси червяка, даст кривую — архимедову спираль. Червяк с такой винтовой поверхностью называют архимедовым. Архимедов червяк в осевом сечении имеет прямолинейный профиль витка, аналогичный инструментальной рейке. Угол между боковыми сторонами профиля витка у стандартных червяков 2а = 40°. Силы в зацеплении В червячном зацеплении (рис. 9.7) действуют: окружная сила червяка Fti, равная осевой силе колеса Fa2,
окружная сила колеса Ft2, равная осевой силе червяка Ffll,
49. Виды разрушения зубьев червячных колес В червячной паре менее прочным элементом является зуб колеса, для которого возможны все виды разрушений и повреждений, встречающиеся в зубчатых передачах, т. е. усталостное выкрашивание, изнашивание, заедание и поломка зубьев (см. § 8.15). Из перечисленного наиболее редко встречается поломка зубьев колеса. В передачах с колесами из оловянных бронз (мягкие материалы) усталостное выкрашивание рабочих поверхностей зубьев колеса наиболее опасно. Возможно и заедание, которое проявляется в намазывании бронзы на червяк; сечение зуба постепенно уменьшается, при этом передача может еще продолжать работать длительное время. Заедание в венцах колес из твердых бронз (алюминиевых) переходит в задир с последующим катастрофическим изнашиванием зубьев колеса частицами бронзы, приварившимися к виткам червяка. Этот вид разрушения зубьев встречается наиболее часто. Для предупреждения заедания рекомендуется тщательно обрабатывать поверхности витков и зубьев, применять материалы с высокими антифрикционными свойствами. Изнашивание зубьев колес червячных передач зависит от степени загрязненности масла, точности монтажа, частоты пусков и остановок, а также от значений контактных напряжений. Излом зубьев червячных колес происходит в большинстве случаев после изнашивания. Червяки современных передач изготавливают из углеродистых или легированных сталей. Наибольшей нагрузочной способностью обладают пары, у которых витки червяка подвергают термообработке до высокой твердости с последующим шлифованием. Червячные колеса изготавливают преимущественно из бронзы, реже из латуни или чугуна. Оловянные бронзы типа ОФ10-1, ОНФ и другие считаются лучшим материалом для червячных колес, однако они дороги и дефицитны.
50 Тепловой расчет червячной передачи. Механическая энергия, потерянная в передаче, превращается в тепловую и нагревает передачу. Если отвод теплоты недостаточный, передача перегревается и выходит из строя. Количество теплоты, выделяющейся в передаче в секунду, или тепловая мощность, Ф=Р1(1-n) Где Р1-мощность на входном валу, n-кпд передачи. Через стенки корпуса редуктора теплота отдается окружающему воздуху, происходит естественное охлаждение. Количество теплоты, отданной при этом в секунду, или мощность теплоотдачи, Ф1=К(t1-t0)А, Где А-площадь поверхности охлаждения, t1-внутренняя температура редуктора или температура масла, t0-температура окружающей среды, К-коэфициент теплоотдачи. Под площадью поверхности охлаждения понимают тольку ту часть площади наружной поверхности корпуса редуктора, которая изнутри омывается маслом или его брызгами, а снаружи-свободно циркулирующим воздухом. По последнему признаку обычно не учитывают площадь поверхности дница корпуса. Если Ф<=Ф1 Это означает, что естественного охлаждения достаточно. В противном случае необходимо применять искусственное охлаждение или снижать мощность передачи. Искусственное охлаждение осуществляют следующими способами: а) обдувом корпуса воздухом с помощью вентилятора, насаженного на вал червяка; в этом случае увеличивается Кф\ б) охлаждением масла водой, проходящей через змеевик; в) применением циркуляционной системы смазки со специальным холодильником.
Планетарные передачи. Классификация. Геометрические и кинематические соотношения. Конструктивные особенности. Планетарными называются передачи, имеющие хотя бы одно из колес перемещающееся вместе со своей геометрической осью относительно центра колеса. Простейший планетарный механизм представляет собой расположенные соосно центральное колесо а, водило h, с сателитом д, свободно вращающейся на оси, установленной на периферии водила. Неподвижная ось колеса, относительно которой вращается водило h, называется основной осью, а колесо а центральное колесо.
Классификация планетарных передач: -по количеству свободных звеньев: планетарные и дифференциальные. -по взаимному расположению осей: с неизменным расположением осей и с изменным. -по количеству ступеней: одноступенчат. и многоступенчат. -по кол-ву связанных между собой планетарных передач: однорядные и многорядные. -по способу соед. рядов: последовательное, параллельное и смешанное. -по типу зубчатых колес: цилиндрические, реечные, конические, комбинированные. -по соотношению выходных характеристик ведомых звеньев: симметричн. и несимметричн. Геометрические и кинематические соотношения. Конструктивные особенности. Конструктивными особенностями планетарных передач является соосность их звеньев, ограниченность числа сателитов, необходимость одновременного их зацепления с несколькими осн.(эл-тами)звеньями. 57.Силы в зацеплении планетарных передач. Расчет на прочность планетарных передач. Планетарными называют передачи, содержащие зубчатые колеса с перемещающимися колесами.
При силовом расчете планетарных передач необходимо учитывать 2 особенности: 1) Нагрузка распределенная по нескольким зацеплениям 2) Каждый сателит нах-ся в зацеплении с 2 колесами Из условия равновесия центрального колеса и сателита получим: (Fga1+Fga2+Fga3)*cosα* Окружная сила на шестерни =Fgt
Напряжения в ремне При работе ременной передачи напряжения по длине ремня распределяются неравномерно (рис. 17.6). Различают следующие виды напряжения в ремне: 1. Предварительное напряжение уп. В состоянии покоя или при холостом ходе каждая ветвь ремня натянута с силой Fo, следовательно,
где А — площадь поперечного сечения ремня.
2. Удельная окружная сила (полезное напряжение) kn. Отношение окружной силы в передаче (полезной нагрузки) Ft к площади поперечного сечения А называют удельной окружной силой kn или полезным напряжением:
Удельная окружная сила kn является разностью напряжений в ведущей уй и ведомой у2 ветвях ремня при рабочем ходе на малой скорости (без учета вли
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 897; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.114.187 (0.021 с.) |


 — условие прочности
— условие прочности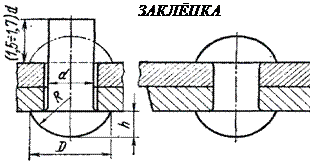 Образуются с помощью специальных деталей – заклёпок [1, 10, 38]. Заклёпка имеет грибообразную форму и выпускается с одной головкой (закладной) вставляется в совместно просверленные детали, а затем хвостовик ударами молотка или пресса расклёпывается, образуя вторую головку (замыкающую). При этом детали сильно сжимаются, образуя прочное, неподвижное неразъёмное соединение.
Образуются с помощью специальных деталей – заклёпок [1, 10, 38]. Заклёпка имеет грибообразную форму и выпускается с одной головкой (закладной) вставляется в совместно просверленные детали, а затем хвостовик ударами молотка или пресса расклёпывается, образуя вторую головку (замыкающую). При этом детали сильно сжимаются, образуя прочное, неподвижное неразъёмное соединение. повышенный расход материала.
повышенный расход материала.



 Образуются выступами на валу, входящими в сопряжённые пазы ступицы колеса. Как по внешнему виду, так и по динамическим условиям работы шлицы можно считать многошпоночными соединениями. Некоторые авторы называют их зубчатыми соединениями.
Образуются выступами на валу, входящими в сопряжённые пазы ступицы колеса. Как по внешнему виду, так и по динамическим условиям работы шлицы можно считать многошпоночными соединениями. Некоторые авторы называют их зубчатыми соединениями.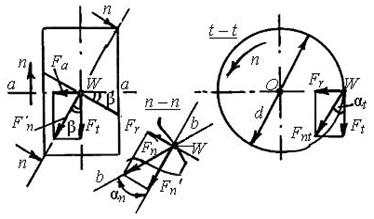









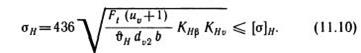


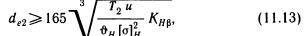










 Звенья вращающиеся вокруг основной оси называются основными звеньями(а,h,д). Если нет заторможенных звеньев, то называется дифферинциальным механизмом.
Звенья вращающиеся вокруг основной оси называются основными звеньями(а,h,д). Если нет заторможенных звеньев, то называется дифферинциальным механизмом.