
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетика лазера в режиме свободной генерации для трехуровневой схемыСодержание книги
Поиск на нашем сайте Рассмотрим временной ход генерации при следующих упрощающих предположениях: а) В лазере возбуждается один собственный тип колебания – мода TEM000 с большим числом квантов (n>>1). В этом случае отпадает необходимость учитывать влияние на временной ход генерации неоднородностей распределения инверсной населенности в объеме активного элемента и связанное с этим то обстоятельство, что каждая мода имеет собственный временной масштаб развития. б) Импульс накачки постоянной интенсивности начинает действовать в момент времени t=0. Потери при этом не зависят от времени. в) Заселенность состояния 2 остается близкой к нулю из-за большой вероятности релаксационного перехода W23, и поэтому он быстро опустошается (см. рис. 1).
д) Начальное распределение возбуждения (инверсной населенности) в активном элементе однородно (равномерно) по его объему. Обозначим Nj – число частиц в единице объема, находящихся на j-ом уровне. Так как N2=0, будем искать заселенности N1 и N3, а также плотность содержащихся в полости резонатора фотонов n(t). В соответствии с пунктом “в” N1+N3≈N, где N – общее число активных (примесных) атомов. Плотность мощности в резонаторе равна Задача заключается в нахождении зависимостей n(t) и N3(t). По сравнению с периодом световых колебаний 1/ω изменение величины n(t) и N3(t) мало. Это видно из уравнения для изменения разности населенностей. Характерные времена больше 1/ω. В то же время величина n(t) очень велика (105÷1018). Известно (см. [1]), что при большом числе квантов (n>>1) поле можно описывать классически. Сказанное характерно для большинства лазерных задач. И в нашем случае мы воспользуемся квазиклассическим подходом, когда электромагнитное поле в резонаторе описывается уравнениями Максвелла, а среда – квантовомеханически. Воспользуемся также упоминавшейся выше “медленностью” функций n(t) иN3(t), что в отношении амплитуды поля E(t) называется приближением “медленных” амплитуд. Этот общеизвестный прием позволяет понизить порядок уравнений для поляризации и электрического вектора, перейти к так называемым укороченным уравнениям, которые в нашем случае будут иметь вид:
Уравнение (1) и (2) впервые были получены и исследованы Статсом и де Марсом в 1960 г. [2] и носят их имя. Эта система описывает нестанционарный режим работы лазера. Первый член в (1) описывает изменение скорости заселенности уровня 3 за счет накачки, второй – за счет спонтанного распада инверсной населенности, третий – за счет индуцированных фотонами в резонаторе лазерных переходов. В уравнении (2) первый член описывает скорость роста интенсивности электромагнитного поля за счет индуцированных (резонансных) переходов, а второй – за счет спонтанных переходов. Последний член очень мал по сравнению с первым, однако именно он обеспечивает начало развития генерации с уровня спонтанного шума. Мы исходили из предположения (см. пункт “б”) о начале накачки в некоторый момент t=0. С момента роста инверсной населенности растет уровень спонтанного шума. На этом этапе происходят и индуцированные спонтанными фотонами переходы. Однако различить их между собой невозможно. При достижении Система уравнений (1)-(2) нелинейная, т.к. содержит члены типа
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 г) Лазерным переходом является переход из состояния 3 в состояние 1.
г) Лазерным переходом является переход из состояния 3 в состояние 1.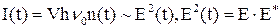 , где V – объем полости резонатора, E(t) – комплексная амплитуда электрической напряженности электромагнитного поля в резонаторе.
, где V – объем полости резонатора, E(t) – комплексная амплитуда электрической напряженности электромагнитного поля в резонаторе. , (1)
, (1) , (2)
, (2) - вероятность рабочего (лазерного) перехода в поле содержащегося в резонаторе излучения, B31 – коэффициент Эйнштейна для индуцированного перехода из состояния 3 в состояние 1, g(ν) – форм-фактор линии рабочего перехода (описывающий форму линии и нормированный на единицу). Из уравнения (2) видно, что при подходящих значениях входящих в него величин может оказаться, что
- вероятность рабочего (лазерного) перехода в поле содержащегося в резонаторе излучения, B31 – коэффициент Эйнштейна для индуцированного перехода из состояния 3 в состояние 1, g(ν) – форм-фактор линии рабочего перехода (описывающий форму линии и нормированный на единицу). Из уравнения (2) видно, что при подходящих значениях входящих в него величин может оказаться, что  . Это означает, что в лазере выполнились условия самовозбуждения электромагнитных колебаний для частоты на максимуме рабочего перехода. Из условия dn/dt=0 определяется параметр,
. Это означает, что в лазере выполнились условия самовозбуждения электромагнитных колебаний для частоты на максимуме рабочего перехода. Из условия dn/dt=0 определяется параметр,  имеющий смысл порогового значения населенности верхнего лазерного уровня
имеющий смысл порогового значения населенности верхнего лазерного уровня  . Из условия баланса мощности накачки и мощности излучения, что также соответствует порогу самовозбуждения,
. Из условия баланса мощности накачки и мощности излучения, что также соответствует порогу самовозбуждения, 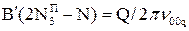 , где Q=2πνooqτэфф – добротность моды TEMooq резонатора, а τэфф – время жизни фотона hνooq в резонаторе.
, где Q=2πνooqτэфф – добротность моды TEMooq резонатора, а τэфф – время жизни фотона hνooq в резонаторе. . Ее решение возможно только путем численных расчетов. При реальных лазерных параметрах (N3>>
. Ее решение возможно только путем численных расчетов. При реальных лазерных параметрах (N3>> 


