
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Указания мер техники безопасностиСодержание книги
Поиск на нашем сайте
1) Лазерная установка ГОС-301 представляет собой ИСТОЧНИК ОПАСНОГО ИЗЛУЧЕНИЯ и электроопасности. 2) Импульсное излучение на выходе лазера невидимо и обладает большой энергией, способной вызвать тепловые ожоги и поражение глаз даже от рассеянного света. 3) В установке имеются конденсаторная батарей общей емкостью 2·10-3 Ф, заряженная до напряжения 3 кВ. При этом в отличие от широко распространенных лабораторных высоковольтных источников в данном случае ток батареи конденсаторов ограничивается не внутренним сопротивлением источника, а внешней нагрузкой. Поледеней при несчастном случае является участки тела попавшие под напряжение. 4) К обслуживанию и эксплуатации лазера допускаются только лица, получившие в результате специального экзамена по технике безопасности допуск к работе с такими установками по группе не ниже IV. СТУДЕНТЫ К самостоятельному УПРАВЛЕНИЮ установкой НЕ ДОПУСКАЮТСЯ. 5) Перед включением лазера проверить установку всех защитных экранов. 6) Перед включением проверить надежность заземления всех приборов установки 7) Работу с лазером при включении питания проводить только в защитных очках со светофильтрами СЗС-22. 8) Наладочные работы, осмотр и ремонт лазера производить только после отключения стойки питания и охлаждения от сети и после разрядки конденсаторов в блоке зажигания разрядной штангой, рассчитанной не напряжение не менее чем 25 кВ. 9) КАТЕГОРИЧЕСКИ ЗАПРЕЩАЕТСЯ: a) Работать при открытых крышках и стенках лазера, при закороченных блокировочных кнопках, а также при неисправных индикаторных пробках и лампах. b) Приступать к работе с лазером без твердого знания принципа работы основных частей. c) Вносить в зону излучения лазера блестящие предметы и производить визуальное наблюдение прямого излучения (даже в защитных очках). d) Работать в режимах, превышающих технические данные лазера. 10) При работе с лазером недопустимо попадание прямого излучения на кожу, особенно на органы зрения. Порядок выполнения работы 1) Повернуть ручку регулятора “Энергия накачки” блока накачки 3 в крайнее левое положение - “0”. 2) Открыть водопроводный кран системы охлаждения. Убедиться в прохождении водопроводной воды в систему слива. 3) Повернуть ключ на пульте управления блока накачки 3 в крайнее правое положение и включить тумблер “Сеть”. 4) Включить тумблер “Охлаждение”. 5) По истечении 10 мин. убедиться во включении второй ступени насоса внутреннего контура системы охлаждения лазерной головки дистиллированной водой. 6) Через зеркало 4 с помощью лазера 9 произвести юстировку лазера. 7) Установить экран перед зеркалом 5. 8) Включить тумблер “Сеть” на блоках питания 3, 10, осциллографе 8, измерителе 6. 9) Присоединить ко входу осциллографа кабель с выхода фотоприемника 7. 10) Нажать кнопку “Заряд конденсаторов”. По окончании заряда нажать кнопку “Поджиг”. Зафиксировать по прибору на пульте пороговую энергию накачки. 11) Определить пороговое значение энергии накачки. Выделить в диапазоне энергий накачки от пороговой до 20 кДж 5 контрольных значений. 12) Снять необходимое количество отсчетов энергии генерации (Еген) для установления ее зависимости от энергии накачки (Енак). 12) Произвести наблюдение по осциллографу и фотографирование осциллограмм с его экрана. Предварительная настройка осциллографа осуществляется регулировкой его чувствительности по входу так, чтобы амплитуда пичков генерации не превышала 3 см. 13) Обработать полученные данные, оценить погрешности измерений. Построить зависимости Еген и длительности общего цуга генерации от Енак. 14) Выключить тумблера “Сеть” всех приборов. Повернуть ключ на пульте в крайнее левое положение. Выключить на пульте тумблер “Охлаждение”. Отключить водопровод. 4. Контрольные вопросы и задания
2) Пользуясь скоростными уравнениями (1) и (2) определить пороговые условия генерации. 3) Каково влияние неоднородности распределения поля в резонаторе на кинетику генерации такого лазера? 4) Объясните модовую структуру поля в конфокальном резонаторе. 5) Каково частотное расстояние между осевыми модами в плоском резонаторе? В конфокальном резонаторе? 6) Каково частотное расстояние между поперечными модами в плоском резонаторе? В конфокальном резонаторе? 7) Каковы поляризационные характеристики излучения Nd3+ лазера на стекле, YAG:Nd3+ лазера, рубинового лазера? 9) Почему длительность импульса генерации лазера ГОС-301 меньше длительности импульса накачки (2 мс)? 10) Рассчитать спектр осевых мод лазера с резонатором, представленным на рис. 6. 11) Определить добротность резонатора лазера с зеркалами R1=32%, R2=41%, R3=0%,? Лабораторная работа №5 Цель работы: изучение пространственной структуры генерации непрерывного He-Ne лазера в зависимости от характеристик его резонатора. Открытые резонаторы Простейший лазерный резонатор состоит из двух плоских или сферических зеркал, установленных параллельно друг другу таким образом, чтобы их оптические оси совпадали. В резонаторе с зеркалами ограниченных размеров пучок не может сохраняться абсолютно сколлимированным из-за дифракционных эффектов. Часть излучения заполнявшего резонатор рассеивается на краях зеркал. Чтобы удержать лазерное излучение внутри резонатора, его зеркала имеют некоторую положительную кривизну (вогнутые зеркала). Можно представить резонатор в виде эквивалентной прозрачной бесконечной среды, содержащей набор линз и диафрагм. В таком резонаторе после многократных прохождений световой волной устанавливается стационарное распределение поля, практически не меняющееся при последующих отражениях. Такой резонатор называется устойчивым, физически это означает, что вследствие периодических фокусировок, поле световой волны сконцентрировано вблизи оси и дифракционные потери невелики. В неустойчивом резонаторе луч по мере прохождения эквивалентной системы линз и диафрагм все более и более расширяется, дифракционные потери в неустойчивом резонаторе велики. Определим аналитические соотношения позволяющие оценить устойчивость резонатора. Пусть имеется открытый оптический резонатор с длинной l, образованный двумя сферическими зеркалами имеющими радиус кривизны R1 и R2 соответственно. Представляя такую систему, с точки зрения распространения оптического излучения в ней, как бесконечный эквидистатнтный ряд линз с фокусными расстояниями F1 и F2, и проводя ее анализ в рамках параксиального приближения, для размеров (r, ρ) светового пятна на зеркалах (линзах) можно получить следующие выражения:
где L - длина резонатора, αn - угол выхода излучения из линзы (отражения от зеркала) определяется следующими выражениями:
После проведения несложных преобразований величину r(ρ) можно определить из следующего рекурсивного соотношения:
Обозначив выражения в скобках g1 и g2 соответственно, неравенства приобретают наглядную интерпретацию в пространстве (g1; g2) изображенную на рис. 1. Другая интерпретация выражения (4) заключается в простом мнемоническом правиле. Если мысленно провести две окружности с диаметрами равными R1 и R2 таким образом, чтобы они касались поверхностей зеркал в центре (см. рис. 2), то для устойчивых резонаторов окружности пересекаются, а для неустойчивых нет. 1.1. Произвольная оптическая волна, введенная в резонатор извне или возбуждаемая внутри, после циклического обхода резонаторной полости вновь вернется в отмеченную точку пространства; при этом характеристики волны в общем случае изменятся. Существует, однако, бесконечный дискретный набор волн, которые в результате различного рода взаимодействий с образующими резонатор элементами в каждом последующем проходе восстанавливают относительное пространственное распределение амплитуды и фазы, а также состояние поляризации в каждом поперечном сечении резонаторной полости. Такие волны называются собственными волнами или собственными типами колебаний (модами) резонатора. В отличие от замкнутых объемных резонансных систем СВЧ диапазона в открытом оптическом резонаторе возбуждаются волны, характеризующиеся почти строго ортогональной ориентацией векторов Е и Н к направлению распространения (ТЕМ-волны). Набег фазы при циклическом проходе собственной волны в стационарном режиме должен быть кратным 2π (целое число длин волн). Это условие определяет резонансную частоту каждого типа колебаний. Совокупность частот собственных волн образует частотный спектр мод. Конкретный характер распределения поля данной моды указывается в обозначении тремя индексами (m, n, q), соответствующими трем ортогональным измерениям резонатора. Продольное (вдоль оси) распределение электромагнитного поля в резонаторе аналогично распределениям, возникающим в замкнутых объемных резонаторах. Совокупность типов колебаний, характеризуемых только продольным индексом (q), называется продольным типом колебаний. Поперечные распределения поля собственных типов колебаний в открытых резонаторах отличаются от периодических распределений, характерных для замкнутых систем. Совокупность типов колебаний, характеризуемых одной парой поперечных индексов (m, n), называется поперечным типом колебаний. В устойчивом резонаторе распределения поля образуют характерные чередования максимумов и минимумов. Характер симметрии распределения поля моды зависит от формы и оптической однородности сечения резонатора. При прямоугольной симметрии индексы (m, n) в обозначении типа колебаний соответствуют числу перемен знака поля вдоль каждой поперечной оси (см. рис. 3). Низший тип колебаний (так называемая основная, или фундаментальная, мода) не содержит изменений знака поля. Гаусовы пучки У лазеров, генерирующих на основной моде, пучок обладает азимутальной симметрией в поперечном сечении с наибольшей интенсивностью на оси. С увеличением расстояния ρ от оси пучка интенсивность падает как exp{-(ρ/a)2}.
Рассмотрим, как меняется с продольной координатой характеристики пучка, интенсивность которого в произвольном сечении описывается функцией Гаусса.
где ρ – поперечная координата, z – продольная координата, а – радиус пучка. Математический аппарат такого распространения приведен в [3]. Как следует из этой работы, пучок имеет перетяжку только в одном месте. Перенесем туда начало координат (см. рис. 6) и пусть
Зависимость радиуса пучка от продольной координаты можно записать в виде
а кривизну волнового фронта пучка
Последние две формулы определяют пространственную структуру TEM - пучка генерации. Характерно следующее: 1) Волновой фронт пучка плоский в точках z=0 и z=∞ и сферический во всех остальных точках. В точке 2) Если в точки
носит название конфокального параметра пучка. 3) При распространении пучка в прозрачной среде, когда интенсивность на оси уменьшается только вследствие дифракционной расходимости, зависимость a(z) имеет вид гиперболы, асимптоты которой наклонены к оси под углами
Эта величина принимается за расходимость TEM00 пучка. При фокусировке гауссовского пучка идеальной линзой (см. рис. 7) меняется его конфокальный параметр, характер распределения интенсивности по сечению сохраняется. Предположим, что имеется пучок с перетяжкой а01. На расстоянии d1 установлена собирающая линза с фокусным расстоянием f. Тогда справа от нее на расстоянии d2 образуется новая перетяжка а02, причем [3]
Особенности фокусировки TEM00 – пучка определяются отношением половины конфокального параметра b/2 к фокусному расстоянию линзы f. Если b>>2f, фокусировка TEM00 – пучка подобна фокусировке широкого “параллельного” пучка света. Если b<<2f, то (7) подобны формулам, описывающим получение изображения с помощью тонкой линзы, если “предметом” считать перетяжку исходного пучка. Однако в любом случае при установке линзы на расстоянии d1=f от перетяжки исходного пучка перетяжка преобразованного пучка будет находиться в правом фокусе линзы: d2=f, а радиус новой перетяжки
где θ1,2 – расходимости исходного и преобразованного пучков. Эта формула может быть использована при измерении расходимости лазерного излучения. При генерации лазером поперечных мод более высокого порядка (TEMmn, m, n ≠ 0) многие характеристики генерации подобны TEM00 – пучку. В частности сохраняется кривизна волнового фронта и характер зависимости R(z). За расходимость TEMmn – пучка принимают угол между направлениями максимальных амплитуд для крайних пятен. Тем самым расходимость TEMmn – пучка оказывается различной для различных направлений. Полная расходимость
где поперечные направления θx, и θy, определяются симметрией в сечении пучка генерации. Для невысоких значений m, n < 4 можно использовать приближенную формулу
где a0 – радиус сечения пучка в перетяжке, m, n ≠ 0. Вообще с увеличением индексов типа колебания m или n расходимость пучка в соответствующем поперечном направлении возрастает. Если задана конфигурация резонатора (см. рис. 1), размер перетяжки TEMmn – пучка можно рассчитать по формуле
где a=R1-L, b=R2-L.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 1) Объясните качественное отличие четырехуровневой схемы от трехуровневой с точки зрения кинетики генерации лазера с импульсной накачкой.
1) Объясните качественное отличие четырехуровневой схемы от трехуровневой с точки зрения кинетики генерации лазера с импульсной накачкой.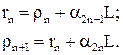 (1)
(1)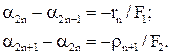 (2)
(2)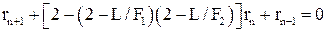 . (3)
. (3) Допуская, что решение имеет вид
Допуская, что решение имеет вид  , а также учитывая, что для ограниченности (устойчивости) размера пятна величина θ должна быть действительной, получаем следующее условие устойчивости резонатора:
, а также учитывая, что для ограниченности (устойчивости) размера пятна величина θ должна быть действительной, получаем следующее условие устойчивости резонатора: . (4)
. (4)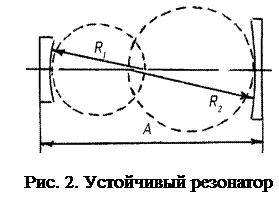 Собственные типы колебаний лазерного резонатора
Собственные типы колебаний лазерного резонатора Такой пучок, показанный на рис. 4, называется Гауссовым. Значение
Такой пучок, показанный на рис. 4, называется Гауссовым. Значение 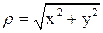 , при котором интенсивность излучения (мощность на единицу площади) уменьшается в е раз по сравнению с интенсивностью на оси пучка, называется поперечным размером пучка (а). Вообще говоря эта величина меняется от точки к точке вдоль оси пучка. В некоторой точке внутри резонатора, называемой шейкой (перетяжкой или горловиной) пучка он имеет минимальный размер а0. Поперечный размер пучка в шейке определяет расходимость лазерного пучка, поскольку внешний пучок в действительности является продолжением внутреннего лазерного пучка за пределами зеркал (см. рис. 5). Дифракционная расходимость характеризуется углом θ~λ/d, где λ – длина волны, d – диаметр отверстия. Для типичного небольшого He-Ne лазера расходимость составляет примерно 1 мрад.
, при котором интенсивность излучения (мощность на единицу площади) уменьшается в е раз по сравнению с интенсивностью на оси пучка, называется поперечным размером пучка (а). Вообще говоря эта величина меняется от точки к точке вдоль оси пучка. В некоторой точке внутри резонатора, называемой шейкой (перетяжкой или горловиной) пучка он имеет минимальный размер а0. Поперечный размер пучка в шейке определяет расходимость лазерного пучка, поскольку внешний пучок в действительности является продолжением внутреннего лазерного пучка за пределами зеркал (см. рис. 5). Дифракционная расходимость характеризуется углом θ~λ/d, где λ – длина волны, d – диаметр отверстия. Для типичного небольшого He-Ne лазера расходимость составляет примерно 1 мрад.
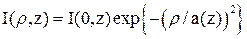 , (5)
, (5) . (6)
. (6)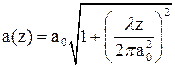 , (7)
, (7)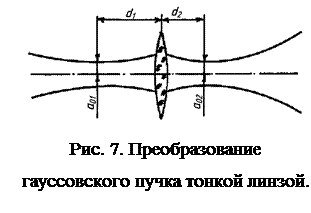
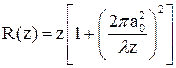 . (8)
. (8) кривизна волнового фронта достигает максимума.
кривизна волнового фронта достигает максимума.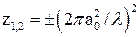 поместить сферические зеркала, радиус кривизны которых равен величине Rmax (см. рис. 6), то данный пучок оказывается собственным типом колебания такого резонатора. Величина
поместить сферические зеркала, радиус кривизны которых равен величине Rmax (см. рис. 6), то данный пучок оказывается собственным типом колебания такого резонатора. Величина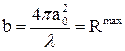 (9)
(9)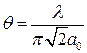 . (10)
. (10)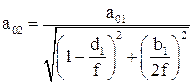 ;
; 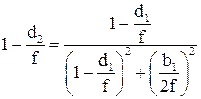 . (11)
. (11)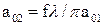 . Воспользовавшись (7) можно рассчитать изменение расходимости TEM00 – пучка, вызванное таким действием линзы
. Воспользовавшись (7) можно рассчитать изменение расходимости TEM00 – пучка, вызванное таким действием линзы , (12)
, (12)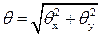 , (13)
, (13) , (14)
, (14)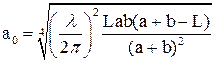 , (15)
, (15)


