
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання до виконання розрахунково-графічного завданняСодержание книги
Поиск на нашем сайте
4. ЗАВДАННЯ ДО ВИКОНАННЯ РОЗРАХУНКОВО-ГРАФІЧНОГО ЗАВДАННЯ 4.1. Перелік тем для виконання теоретичної частини
1. Суттєва характеристика господарських рішень і технологія прийняття рішень господарської діяльності. 2. Обґрунтування господарських рішень і оцінювання їх ефективності. 3. Прогнозування та аналіз господарських рішень. 4. Критерії прийняття рішень в умовах невизначеності. 5. Підприємницькі ризики та їх вплив на прийняття господарських рішень. 6. Критерії прийняття господарських рішень в умовах ризику. 7. Обґрунтування фінансових та інвестиційних рішень в умовах ризику. 8. Якісне оцінювання підприємницьких ризиків. 9. Кількісне оцінювання підприємницьких ризиків. 10. Основи ризик-менеджменту.
4.2. Завдання для виконання розрахункової частини Завдання 1 Компанія «Атекс» купує оптові партії бананів та реалізує їх в роздріб. Витрати на купівлю бананів (включаючи транспортування) складають 40 гривень за ящик. Ціна реалізації за ящик складає 100 гривень (наведені дані використовуються для прикладу вирішення). Компанія розглядає можливість укладення довгострокового контракту з постачальником. Задача економіста компанії : проаналізувавши інформацію про попит на банани, дати рекомендації стосовно вибору стратегії компанії щодо закупівлі бананів. Нижче наведений приклад вирішення цієї задачі. Уважно ознайомтесь з прикладом, звертаючи увагу на визначення та формули. На основі даних , наведених у таблиці 4.1 (де N є останньою цифрою залікової книжки студента (слухача)), необхідно :
1. Розрахувати ü прибуток (збиток) при різних обсягах купівлі та продажу бананів з урахуванням цін закупівлі та реалізації бананів; ü очікуваний прибуток (збиток) з урахуванням ймовірності попиту бананів за минулі періоди; ü стандартне відхилення від очікуваної величини прибутку та коефіцієнт варіації для кожного із варіантів, розглянутих економістом компанії; ü очікувану вартість точної інформації, надану фірмою «АІВ».
2. Вибрати стратегію компанії відносно закупівлі бананів. Дані розрахунків доцільно розмістити у вигляді таблиць.
3. Відобразити розрахунки пошуку оптимального рішення щодо закупівлі бананів у вигляді «дерева рішень».
Таблиця 4.1 – Вихідні данні завдання 1 Показники Вихідні дані Ціна закупівлі 1 ящика бананів, грн 50 + N Ціна продажу 1 ящика бананів, грн 110 - N Показник
умова Імовірність попиту за минулі періоди (Pi) Імовірність попиту за даними фірми «АІВ» (P1i) 100 ящиків щотижнево 10 % 40 % 200 ящиків щотижнево 30 % 30 % 300 ящиків щотижнево 40 % 20 % 400 ящиків щотижнево 20 % 10 % Приклад рішення Завдання пов’язано з вирішенням задачі в умовах невизначеності. Невизначеність пов’язана з наявністю можливих випадкових подій. Тому передусім слід встановити ці можливі випадкові події та визначити їх Імовірність. Імовірність випадкової події (А) – це відношення числа сприятливих наслідків випробування (m) до загального числа усіх можливих наслідків (n). Р (А) =ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Умовою завдання ці випадкові події установлені: ми розглядаємо основне завдання (рішення відносно закупівлі бананів) в залежності від подій - попиту на банани. Імовірність подій, яка визначена за допомогою математичних розрахунків або на основі статистичних спостережень минулих подій, є об’єктивною ймовірністю. Наявність інформації про Імовірність релевантних явищ дозволяє визначити очікувані результати майбутніх подій з урахуванням ймовірності можливих подій. Очікувана величина – це сума можливих значень змінної величини , зважених за допомогою їх ймовірності. Очікувана величина визначається формулою: Ā = де Ā –очікувана величина; Аi – значення змінної величини для певної події (i); Pi –Імовірність певної події (i). Спеціалісти компанії, які дослідили продаж бананів за попередні періоди, визначили можливий попит на банани та його ймовірність (табл. 4.2), а також розрахували прибуток при різних обсягах закупівлі бананів (табл.4.3). Таблиця 4.2 – Розподіл ймовірності попиту на банани Тижневий попит (ящиків) – (i) Імовірність попиту (Pi) 100 (i1) 0,20 (P1) 200 (i2) 0,40 (P2) 300 (i3) 0,30 (P3) 400 (i4) 0,10 (P4)
Таблиця 4.3 - Розрахунок прибутку при різних обсягах закупівлі та попиту Тижневий попит (ящиків) – (i) Обсяг закупівлі (ящиків) ) – (j) 100 (j1) 200 (j2) 300 (j3) 400 (j4) Прибуток, грн. (Aij) 100 (i1) 6 000 2 000 -2 000 -6 000 200 (i2) 6 000 12 000 8 000 4 000 300 (i3) 6 000 12 000 18 000 14 000 400 (i4) 6 000 12 000 18 000 24 000
Виходячи із даних таблиць 4.2 та 4.3 можливо розрахувати очікуваний прибуток (збиток) при різних обсягах закупівлі. У таблиці 4.4 зібрані дані розрахунку очікуваного прибутку при обсязі закупівлі 200 ящиків на тиждень.
Таблиця 4.4 - Очікуваний прибуток при обсязі купівлі 200 ящиків на тиждень Тижневий попит (ящиків) – (i) Прибуток, грн. (Ai) Імовірність попиту (Pi) Очікуваний прибуток, грн. Ā 100 (i1) 2 000 0,20 200 (i2) 12 000 0.40 4 800 300 (i3) 12 000 0,30 3 600 400 (i4) 12 000 0,10 1 200
10 000(Ā)
Аналогічно можливо розрахувати очікуваний прибуток (збиток) при інших обсягах закупівлі. Результати розрахунків приведені у таблиці 4.5.
Таблиця 4.5 - Розрахунок очікуваного прибутку (збитку) Тижневий попит (ящ.) – (i) Імовірність попиту (Pi) Обсяг закупівлі (ящиків) – (j) 0,20 1 200 -400 -1 200 0.40 2 400 4 800 3 200 1 600 0,30 1 800 3 600 5 400 4 200 0,10 1 200 1 800 2 400 Загальний очікуваний прибуток (збиток) -Ā 6 000 10 000 10 000 7 000 Більш наглядно розрахунок очікуваного прибутку для кожного із існуючих варіантів дій може бути представлений у вигляді «дерева рішень» (рис. 4.1).
Дерево рішень - це діаграма, що відображає декілька можливих дій, можливих подій, а також потенціальні результати кожного напрямку дій. Наведені розрахунки (рис. 1.1) показують, що у разі закупки 200 та 300 ящиків бананів прибуток кожного тижня складатиме 10 000 гривень.
ДЕРЕВО РІШЕНЬ
Дія (купівля) Подія (попит) Результат (прибуток) Імовірність Очікуваний прибуток 100 6 000 0,20 1 200 6 000 0.40 2 400 6 000 0,30 1 800 6 000 0,10
6 000 200 2 000 0,20 12 000 0.40 4 800 12 000 0,30 3 600 12 000 0,10 1 200
10 000 300 -2 000 0,20 -400 8 000 0.40 3 200 18 000 0,30 5 400 18 000 0,10 1 800
10 000 400 -2 000 0,20 -1 200 4 000 0.40 1 600 14 000 0,30 4 200 24 000 0,10 2 400
7 000 Рис.4.1 - Дерево рішень відносно обсягів закупівлі бананів
Але необхідно врахувати не тільки абсолютне значення очікуваного результату, а й можливе відхилення від очікуваної величини, яке характеризує величину ризику. Стандартне відхилення (s)рахується як квадратний корінь середньо квадратичного відхилення від очікуваної величини. s= Розрахуємо стандартне відхилення від очікуваного прибутку для кожного із основних варіантів, розмістивши у вигляді таблиці 4.6 для порівняння результатів.
Таблиця 4.6 - Стандартне відхилення від очікуваного прибутку Закупівля 200 ящиків бананів за один тиждень,грн. Закупівля 300 ящиків бананів за один тиждень,грн (2 000-10 000)2х0,2= 12 800 000 (-200-10 000)2х0,2= 28 800 000 (12 000-10 000)2х0,4= 1 600 000 (8 000-10 000)2х0,4= 1 600 000 (12 000-10 000)2х0,3= 1 200 000 (18 000-10 000)2х0,3= 19 200 000 (2 000-10 000)2х0,1= 400 000 (18 000-10 000)2х0,1= 6 400 000 Всього: 16 000 000 Всього: 56 400 000 s= s= Висновок: при тому що два варіанти мають однаковий очікуваний прибуток, необхідно закупати 200 ящиків бананів щотижнево, тому що стандартне відхилення в цьому випадку менше.
Загальні правила прийняття рішень в умовах невизначеності можливо сформулювати так: 1. Якщо альтернативні дії мають однакову очікувану величину, то вибирають дію з найменшим стандартним відхиленням. 2. Якщо альтернативні дії мають однакове стандартне відхилення, то вибирають дію з найбільшим очікуваним прибутком або з найменшим очікуваним збитком. 3. Якщо альтернативні дії мають різну очікувану величину та різне стандартне відхилення, то вибирають дію з найменшим коефіцієнтом варіації. Коефіцієнт варіації (Кv) – це відношення стандартного відхилення та очікуваного прибутку.
Кv = Чим менше значення коефіцієнта варіації, тим менший ризик. У нашому прикладі коефіцієнт варіації для двох основних варіантів дорівнює: Закупівля 200 ящиків бананів Кv = 4000 : 10 000=0,40 Закупівля 300 ящиків бананів Кv =7 483: 10 000=0,75 У прикладі імовірність майбутнього попиту була визначена на основі інформації про обсяги продаж в минулі періоди. Але попередній опит не гарантує точного результату розрахунків майбутнього обсягу продажу. Тому, якщо існує можливість отримати точнішу інформацію про майбутні події, її слід використати. Очікувана вартість точної інформації - це максимальна ціна, яка може бути виплачена за додаткову інформацію про події, котрі невідомі тому, хто приймає рішення. Очікувана вартість точної інформації дорівнює різниці між очікуваною вартістю з додатковою інформацією та очікуваною вартістю з наявною інформацією. Припустимо, що консалтингова фірма «АІВ» може надати компанії «Атекс» інформацію про попит, який завжди буде забезпечувати прийняття оптимального рішення щодо обсягу закупівлі бананів. Розрахунок очікуваної вартості точної інформації може бути представлений у вигляді таблиці 4.7.
Таблиця 4.7 - Розрахунок очікуваної вартості Розрахунок очікуваної вартості точної інформації: Тижневий попит бананів (i) (Āmax), грн (P1i) (A 1i) 100 ящиків 6 000 20 % 6 000 х 0,2 = 1 200 грн 200 ящиків 12 000 40% 12 000 x 0,4 = 4 800 грн 300 ящиків 18 000 30% 18 000 х 0,3 = 5 400 грн 400 ящиків 24 000 10% 24 000 х 0,1 = 2 400 грн Очікувана вартість з додатковою інформацією (A 1i) 13 800 грн Очікувана вартість з наявною інформацією(Ai) 10 000 грн Очікувана вартість точної інформації 3 800 грн
Таким чином, максимальна сума, яка може бути сплачена за додаткову інформацію про попит на банани, складе 3 800 грн. У ситуації, коли немає можливості оцінити Імовірність майбутніх подій, менеджер може вибрати одну з трьох стратегій: - максимізація максимальних результатів; - максимізація мінімальних результатів; - мінімізація максимального втрат. Стратегія 1. Максимізація максимальних результатів
Максимізація максимальних результатів - це оптимістичний прогноз, який передбачає найкращий результат. Таблиця 4.8 – Дані прибутку в залежності від обсягу щотижневої закупівлі Обсяг щотижневої закупівлі (ящиків) Максимальний прибуток, грн 6 000 12 000 18 000 24 000
З табл. 4.8 видно, що в нашому прикладі менеджер-оптиміст може прийняти рішення купувати 400 ящиків бананів щотижня, оскільки він сподівається отримати максимальний прибуток 24 000 грн. Втім , вибираючи таку стратегію, варто пригадати таке висловлювання: «Вірити в те, що подія відбудеться тому, що ти цього бажаєш, - безглуздо ».
Стратегія 2. Максимізація мінімальних результатів
Максимізація мінімальних результатів - це песимістичний прогноз, який допускає найгірший результат. Таблиця 4.9– Дані прибутку в залежності від обсягу щотижневої закупівлі Обсяг щотижневої закупівлі (ящиків) Мінімальний прибуток (збиток), грн 6 000 2 000 -2 000 -6 000 Менеджер-песиміст керується законом Паддера, який говорить: «Все, що добре починається, закінчується погано. Все, що починається погано, закінчується ще гірше». Тому такий менеджер, проаналізувавши дані таблиці 4.9, прийме рішення купувати 100 ящиків бананів щотижня. Стратегія 3. Мінімізація максимальних втрат.
В основу цієї стратегії покладено закон Мерфі: «Якщо якась неприємність може трапитися, вона неодмінно трапиться». Мінімізація максимальних втрат - це метод оцінки, за допомогою якого визначаються можливі втрати через нестачу запасів і реальну вартість зайвих запасів. Цей метод передбачає визначення збитку виходячи з реальних витрат внаслідок закупівлі зайвих запасів і можливої втрати прибутку внаслідок закупівлі запасів у кількості, що не задовольняє попит. Наприклад, у разі придбання 300 ящиків бананів при попиті 100 ящиків 200 ящиків бананів не будуть реалізовані, а компанія втратить 8 000 грн
Таблиця 4.10 - Розрахунок збитку в умовах дискретної ситуації Щотижневий попит (ящиків) Обсяг щотижневої закупівлі (ящиків) 4 000 8 000 12 000 6 000 4 000 8 000 12 000 6 000 4 000 18 000 12 000 6 000 Максимально можливий збиток, грн. 18 000 12 000 8 000 12 000
ВИСНОВОК: Наведені розрахунки показують, що згідно з принципом мінімізації максимальних втрат слід купувати 300 ящиків бананів щотижня.
Завдання 2 Фірма переглядає свою цінову політику.На товар А вводиться нова ціна. У разі її адаптації на ринку фірма буде мати додатковий прибуток, якщо споживач не готовий до зміни ціни - фірма зазнає збитків (розмір прибутку і втрат вказаний в таблиці 4.11). Імовірність прибутку і втрат дорівнює 0,5 і 0,5. Номер варіанта відповідає останній цифрі залікової книжки студента (слухача). Необхідно: визначити найбільш доцільне управлінське рішення, використовуючи дерево рішень. Таблиця 4.11 – Вихідні дані завдання 2 № варіанта Величина показника Збиток, тис. грн Прибуток, тис. грн Завдання 3 Досліджуються два інвестиційні проекти - А і Б. Кількість випадків спостережень (Ni), а також прибутки (Аi) в результаті вкладення в проекти А і Б,наведено в таблиці 4.12. Номер варіанта відповідає останній цифрі залікової книжки студента (слухача). Який проект буде кращим для капіталовкладень? Необхідно: визначити імовірність отримання прибутку, враховуючи кількість випадків спостережень, середню величину прибутку з кожного інвестиційного проекту, ступінь ризику, відносну оцінку ризику. Зробити висновок щодо привабливості капіталовкладень в проект А чи Б?
Таблиця 4.12 – Вихідні дані завдання 3 № варіанта
Величина показників ПРОЕКТ «A» N1a Прибуток (А1а) N2a Прибуток (А2а) N2a Прибуток (А3а) ПРОЕКТ «Б» N1б Прибуток (А1б) N2б Прибуток (А1б) N3б Прибуток (А1б)
Завдання 4 Підприємство має 2 варіанти виробництва і реалізації товарів. За прогнозними даними доходи від реалізації обох видів товарів у вдалому та невдалому випадках наведені в таблиці 4.13 (N – остання цифра номера залікової книжки студента (слухача)). Необхідно: оцінити ризик, обґрунтувати та ухвалити рішення, який вид товарів (1 чи 2) виробляти.
Таблиця 4.13 - Варіанти виробництва і реалізації товарів Варіанти виробництва і реалізації товарів Вдалий випадок Невдалий випадок Імовірність Дохід Імовірність Дохід 1 вид товарів 0,6 205+N 0,4 95+N 2 вид товарів 0,97 165+N 0,03 65+N
Завдання 5 Підприємець займається реалізацією полуниці: скуповує по 15 гривен за кошик і продає по 25 гривен за кошик. За кожний з 40 днів «сезону полуниці» він реалізовував різну кількість кошиків. Це зумовлено випадковістю попиту на цей товар. Торговець помітив, що попит обсягом 4 кошики спостерігався 4 дні, 5 кошиків — 8 днів, 6 — 16 днів, 7 — 10 днів, 8 — 2 дні.
Необхідно: побудувати платіжну матрицю доходів та матрицю ризиків і за допомогою різних критеріїв визначити оптимальну кількість товару, яку необхідно закуповувати підприємцю. Примітка. Уважно ознайомтесь з матеріалом до вирішення завдання. Використовуйте його для розрахунків . Вибір критеріїв завдання здійснюється, виходячи з табл. 4.14. Номер варіанта відповідає останній цифрі залікової книжки студента (слухача).
Таблиця 4.14 – Вибір варіанта завдання 5 Правило (критерій) № варіанта Критерій Лапласа 1; 3; 5; 7; 9 Критерій Вальда Правило максимакс Критерій Севіджа 0, 2, 4, 6, 8 Критерій Гурвіца (коефіцієнт песимізму = 0,5) Критерій Байєса
Матеріал до вирішення завдання
Багато рішень у підприємницькій діяльності доводиться приймати в умовах, коли необхідно вибирати напрями дій з декількох можливих варіантів, результати здійснення яких важко спрогнозувати. Невизначеність виступає основною характеристикою недостатньої забезпеченості процесу прийняття економічних рішень знаннями щодо певної проблемної ситуації. На теоретичному рівні ця ситуація досить добре розроблена, проте на практиці застосування формалізованих алгоритмів аналізу обмежене. Основні труднощі полягають у тому, що неможливо оцінити ймовірність появи наслідків прийнятих рішень. Для вибору оптимальної стратегії в ситуації невизначеності використовують декілька критеріїв. Кожен з критеріїв передбачає як оптимальне рішення використовувати тільки одну конкретну стратегію («чисту» стратегію). Але в деяких випадках краще не дотримуватися одної стратегії, а застосовувати декілька («мішану» стратегію). За наявної кількох альтернативних станів зовнішнього середовища і внутрішніх умов підприємства, їм відповідають належні значення цільових функції. Якщо жодна з альтернатив не домінуватиме, то постає задача вибору рішення із застосуванням правил і критеріїв теорії прийняття рішень. Наведемо кілька загальних критеріїв раціонального вибору варіантів рішень з безлічі можливих. Критерії засновані на аналізі матриці можливих станів навколишнього середовища й альтернатив рішень. Для прийняття рішень в умовах невизначеності та ризику за допомогою статичної ігрової моделі вхідна інформація подається у вигляді матриці, рядки якої — це можливі альтернативні рішення, а стовпчики — стани системи (середовища).Кожній альтернативі рішення і кожному стану системи (середовища) відповідає результат (наслідок рішення), який визначає витрати або виграш за вибору даної альтернативи рішення та реалізації даного стану системи. У дискретному випадку дані задаються у формі матриці, представленої в табл. 4.15.
Таблиця 4.15 – Матриця прибутків
S1 … Sm A1 a11 … a1m … … … … An an1 … anm
де: Аі—альтернатива і-го рішення (і = n); Si —можливий j-стан навколишнього середовища (j = 1,m); aij— результат (наслідок рішення). У загальному вигляді aij — неперервна функція аргументів Аі та Si, що позначає вартість капіталу, прийняту альтернативою j за стану навколишнього середовища і. Для вибору оптимальної стратегії в ситуації невизначеності та ризику використовуються різні правила та критерії.
Уважно ознайомтеся з прикладом вирішення завдання за різними критеріями. Приклад вирішення (умови завдання).
Фірма планує реалізацію своєї продукції на ринках, враховуючи можливі варіанти купівельного попиту Пj, j=1,4 (низький, середній, високий, дуже високий). На підприємстві розроблено три стратегії збуту товарів A1, А2, А3. Обсяг товарообігу (в грошових одиницях), залежний від стратегії і купівельного попиту, представлений в таблиці (N=3):
Таблиця 4.16 – Вихідні дані приклада Аj Пj П1 П2 П3 П4 А1 30 +N 25 + N/2 А2 70 - N 10 + N/2 А3 25 – N/2 60 - N Відомі можливі стани купівельного попиту, які відповідно q1=0,3, q2=0,2, q3=0,4, q4=0,1. Необхідно: знайти стратегію збуту, що максимізувала середній товарообіг фірми. При цьому використовувати критерії Вальда, Гурвіца, Севіджа, Байєса. Рішення за критерієм Байєса. По критерію Байєса за оптимальну вибирається та стратегія (чиста) Ai, при якій максимізовується середній виграш а або мінімізується середній ризик r. Рахуємо значення ∑(aijpj) : ∑(a1,jpj) = 33•0.3 + 10•0.2 + 20•0.4 + 26.5•0.1 = 22.55 Складаємо матрицю: Ai П1 П2 П3 П4 ∑(aijpj) A1 9.9 2.65 22.55 A2 13.4 4.6 2.5 35.5 A3 7.05 5.85 35.9 pj 0.3 0.2 0.4 0.1 Висновок: вибираємо стратегію N=3. Рішення за критерієм Лапласа. Якщо вірогідність станів природи правдоподібна, для їх оцінки використовують принцип недостатньої підстави Лапласа, згідно якого всі стани природи вважаються рівноімовірними, тобто: q1 = q2 = ... = qn = 1/n. qi = 1/4
Складаємо матрицю: Ai П1 П2 П3 П4 ∑(aij) A1 8.25 2.5 6.63 22.38 A2 12.5 16.75 2.88 6.25 38.38 A3 5.88 8.75 14.63 39.25 pj 0.25 0.25 0.25 0.25 Висновок: вибираємо стратегію N=3. Рішення за критерієм Вальда (правило крайнього песимізму). По критерію Вальда за оптимальну береться чиста стратегія, яка в найгірших умовах гарантує максимальний виграш, тобто a = max(min aij). Критерій Вальда орієнтує статистику на найбільш несприятливі стани природи, тобто цей критерій виражає песимістичну оцінку ситуації.
Складаємо матрицю: Ai П1 П2 П3 П4 min(aij) A1 26.5 A2 11.5 11.5 A3 23.5 58.5 23.5 Висновок:число 23,5 є максимальним, тому вибираємо стратегію N=3.
Рішення за критерієм Севіджа (правило мінімальних ризиків). Критерій Севіджа рекомендує вибирати як оптимальну стратегію ту, при якій величина максимальних ризиків мінімізується в найгірших умовах, тобто забезпечується: a = min(max rij). Критерій Севіджа орієнтує статистику на найбільш несприятливі стани природи, тобто цей критерій виражає песимістичну оцінку ситуації. При вживанні цього правила аналізується матриця ризиків. Знаходимо матрицю ризиків. Ризик – міра невідповідності між різними можливими результатами прийняття певних стратегій. Максимальний виграш в j-м стовпці bj = max(aij) характеризує сприятливість стану природи. 1. Розраховуємо 1-й стовпчик матриці ризиків: r11 = 50 - 33 = 17; 2. Розрахуємо 2-й стовпчик матриці ризиків: r12 = 67 - 10 = 57; 3. Розрахуємо 3-й стовпчик матриці ризиків: r13 = 40 - 20 = 20; 4. Розрахуємо 4-й стовпчик матриці ризиків: r14 = 58.5 - 26.5 = 32; Складаємо матрицю ризиків: Ai П1 П2 П3 П4 max(aij) A1 A2 28.5 33.5 33.5 A3 26.5 Висновок: число 32 є максимальним, тому вибираємо стратегію N=3. Рішення за критерієм Гурвіца (правило, що зважує песимістичний і оптимістичний підходи до ситуації). Критерій Гурвіца є критерієм песимізму - оптимізму. Приймається рішення , за яким досягається максимуму. За оптимальну приймається та стратегія, для якої виконується співвідношення: max(si), де si = y min(aij) + (1-y)max(aij). При у = 1 отримаємо критерій Вальда, при у = 0 отримаємо – оптимістичний критерій (максимакс). Критерій Гурвіца враховує можливість як найгіршої, так і найкращої для людини поведінки природи. Як вибирається у? Чим гірше наслідки помилкових рішень, тим більше бажання застрахуватися від помилок, тим у ближче до 1. Розраховуємо si : s1 = 0.5•10+(1-0.5)•33 = 21.5 Складаємо матрицю: Ai П1 П2 П3 П4 min(aij) max(aij) y min(aij) + (1-y) max(aij) A1 26.5 21.5 A2 11.5 11.5 39.25 A3 23.5 58.5 23.5 58.5 Висновок: вибираємо стратегію N=3. Таким чином, в результаті вирішення статистичної гри по різних критеріях частіше за інших рекомендувалася стратегія A3. Список джерел 1. Азаренкова Г. М. Аналіз моделювання і управління ризиком (в схемах та прикладах) : навч. посіб. / Г. М. Азаренкова. – Львів : Новий світ-2000, 2011. – 240 с. 2. Андрєєва Т. Є. Ризик у ринковій економіці : навч. посіб. / Т. Є. Андрєєва, Т. Е. Петровська. – Х. : Бурун Книга, 2005. – 128 с. 3. Донець Л. І. Економічні ризики та методи їх вимірювання : [навч. посіб.] / Л. І. Донець. – К. : Центр навчальної літератури, 2006. – 312 с. 4. Івченко І. Ю. Моделювання економічних ризиків і ризикових ситуацій : навч. посіб. / І. Ю. Івченко. – К. : ЦУЛ, 2007. – 344 с. 5. Кондрашихін А. Б. Теорія та практика підприємницького ризику (Авторизований доступ) : навч. пос. / А. Б. Кондрашихін, Т. В. Пепа. – К. : ЦУЛ, 2009. – 224 с. 6. Клименко С. М. Обґрунтування господарських рішень та оцінка ризиків : навч. метод. посіб. для сам. вивч. дисц. / С. М. Клименко, О. С. Дуброва. – К. : КНЕУ, 2006. – 188 с. 7. Кузьмін О. Є. Обґрунтування господарських рішень і оцінювання ризиків : навч. посіб. / О. Є. Кузьмін, Г. Л. Вербицька, О. Г. Мельник. – Львів : Нац. ун-т «Лівівська політехніка», 2008. – 212 с. 8. Лук'янова В. В. Економічний ризик : навч. посіб. / В. В. Лук'янова, Т. В. Головач. – К. : Академвидав, 2007. – 464 с. 9. Мороз О. Оптимальне управління економічними системами в умовах невизначеності та ризику : монографія / О. Матвійчук, А. Мороз. – Вінниця : Універсум, 2003. – 177 с. 10. Останкова Л. А. Аналіз, моделювання та управління економічними ризиками : навч. посіб. / Л. А. Останкова, Н. Ю. Шевченко. – К. : ЦУЛ, 2011. – 256 с. 11. Сараєва І. М. Системне моделювання процесу ідентифікації підприємницьких ризиків : [монографія] / І. М. Сараєва; ІПРЕЕД НАНУ. – О. : Фенікс, 2007. – 188 с. 12. Старостіна А. О. Ризик-менеджмент: теорія та практика : навч. посіб. / А. О. Старостіна, В. А. Кравченко. – К. : Політехніка, 2004. – 200 с. 13. Ступаков В. С. Риск-менеджмент : учеб. пособие / В. С. Ступаков, Г. С. Токаренко. – М. : Финансы и статистика, 2007. – 288 с. 14. Управління підприємницьким ризиком / за заг. ред. д-ра екон. наук Д. А. Штефанека. – Тернопіль : Економічна думка, 1999. – 224 с. 15. Чорноморченко Н. В. Обґрунтування господарських рішень і оцінювання ризиків : навч.-метод. посібник для сам. вивчення дисц. / Н. В. Чорноморченко, І. С. Іванова, Н. С. Приймак. – Львiв : Магнолiя-2006, 2010. – 260 с. 16. Шегда А. В. Ризики в підприємництві: оцінювання та управління : навч. посіб. / А. В. Шегда, М. В. Голованенко ; за ред. А. В. Шегди. – К. : Знання, 2008. – 271 с. Навчальне видання
МЕТОДИЧНІ ВКАЗІВКИ до виконання розрахунково-графічного завдання з дисципліни «Обґрунтування господарських рішень і оцінювання ризиків» (для студентів освітньо - кваліфікаційного рівня «бакалавр» напряму підготовки 6.030504 – «Економіка підприємства» і слухачів другої вищої освіти спеціальності 7.03050401 - «Економіка підприємства»)
Укладачі: ПетроваВалентина Федорівна
Відповідальний за випуск А. Є. Ачкасов Редактор О. В. Тарасюк Комп’ютерне верстання Ю. В. Горєлкіна
План 2013, поз.565М __________________________________________________________________ Підп. до друку 27.09.2013 Формат 60х84 1/16. Друк на ризографі Тираж 50 пр. Зам.№ Ум. друк. арк.1,5
Видавець і виготовлювач: Харківський національний університет міського господарства імені О. М. Бекетова вул. Революції, 12, Харків, 61002 Електронна адреса: rectorat@kname.edu.ua Свідоцтво суб’єкта видавничої справи: ДК №4064 від 12.05.2011р.
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.54.100 (0.014 с.) |

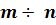 (4.1)
(4.1)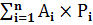 (4.2)
(4.2)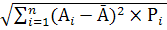 (4.3)
(4.3)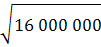 = 4 000
= 4 000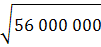 = 7 483
= 7 483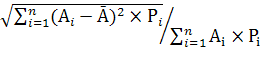 = s
= s 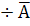 (4.4)
(4.4)


