
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
b)Тәуелсіз және тәуелді оқиғалар.Содержание книги
Поиск на нашем сайте
Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертпесе, ондай екі оқиғаны тәуелсіз деп атайды.Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай оқиғаны тәуелді оқиғалар деп атайды.А оқиғасының пайда болуы В оқиғасының пайда болуына байланысты, яғни А оқиғасының пайда болу ықтималдығы Воқиғасының пайда болуына байланысты өзгереді. Мұндай ықтималдықты шартты ықтималдық деп атайды. Шартты ықтималдықты былай белгілейді:
c)Толық ықтималдық Айталық, Н1, Н2, ...,Нп оқиғалары қос-қостан үйлесімсіз оқиғалардың толық тобын құрайтын болсын. Ал В оқиғасы осы оқиғалардың тек біреуімен ғана бірігіп орындалады дейік. Оның үстіне р(Н1), р(Н2), ...,р(Нп) және
Көбейту теоремасы бойынша
Демек, немесе жоғарыдағы берілгендері бойынша В-нің ықтималдығын осы (2) формуламен анықтайды. Бұл формуланы ықтималдықтардың толық формуласы деп атайды. Әдетте, Н1, Н2, ...,Нп оқиғаларын гипотезалар (болжамдар) деп атайды. Байес формуласы.Осы уақытқа дейін қарастырып келген ықтималдықтар интуитивті түрде теориялық болжамдарға сүйеніп, тәжірибе жүргізбей-ақ, комплекс шарт жөніндегі білім (түсінік) негізінде анықталып келді. Тәжірибеге дейінгі Н1, Н2, ...,Нп гипотезалар (оқиғалар) ықтималдығы сәйкес түрде р(Н1), р(Н2), ...,р(Нп) болатынды. Тәжірибе жүргізілді делік, соның нәтижесінде В оқиғасының пайда болғаны анықталды, енді осы В оқиғасының пайда болуына байланысты Н1, Н2, ...,Нп гипотезаларының ықтималдығын қайта қарауға тура келеді. Яғни Тәуелді оқиғалар В мен
Бұдан шығады. Бұл формулаға толық ықтималдық формуласынан шығады. Осы (3) формуланы Байес формуласы деп айтады.P(Hi) ықтималдықтары гипотезалардың априорлы (тәжірибеге дейінгі) ықтималдықтары,ал PB(Hi)-апостериорлы (тәжірибеден кейінгі) ықтималдықтары деп аталады. 18.Қайталанбалы тәуелсіз сынақтар. Бернули формуласы. Тәуелсіз п рет тәжірибе жасадық дейік. Әр жолы ізделінді А оқиғаның пайда болу ықтималдығы тұрақты
Осы формуланы Бернулли формуласы деп атайды. Муавр-Лапластың шектік теориясыТеория-1. Айталық 0<p<1 болсын. Онда |k-np|=o((npq
Яғни n {k;|k-np| Мұндағы Теореманы дәлелдемес бұрын мынаған назар аударайык: егер функциясын және 1`-теорема. 0<p<1 болсын . онда барлық
Лапластың интегралдық теоремасы тәуелсіз n рет тәжірибе жасағанда ізделінді А оқиғаның пайда болу ықтималдығы тұрақты Р(А)=p болсын. Онда А оқиғасының пайда болу саны Pn(k1,k2)≈Ф(х2) – Ф(х1) мұндағы Ф(х)=
N артқан сайын муавр-лаплас формуласына мәні дәлірек болады және бұл формуланы npq
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.86.160 (0.01 с.) |

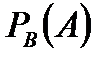 - В оқиғасы орындалғанда А оқиғасының пайда болу ықтималдығы.
- В оқиғасы орындалғанда А оқиғасының пайда болу ықтималдығы.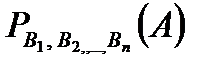 -
- 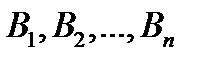 оқиғалары орындалғанда А оқиғасының пайда болу ықтималдығы.
оқиғалары орындалғанда А оқиғасының пайда болу ықтималдығы.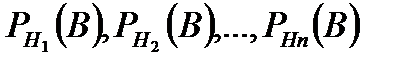 ықтималдықтары белгілі болсын. ықтималдықтың толық формуласы Шынында
ықтималдықтары белгілі болсын. ықтималдықтың толық формуласы Шынында 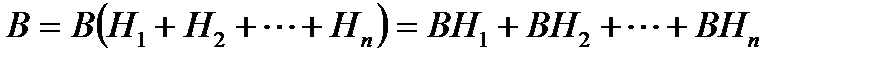 (1)Ал Н1, Н2, ...,Нп қос-қостан үйлесімсіз болғандықтан,
(1)Ал Н1, Н2, ...,Нп қос-қостан үйлесімсіз болғандықтан, 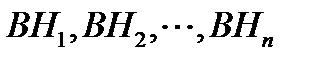 оқиғалары да қос-қостан үйлесімсіз. Олай болса, бұл оқиғаларға қосу теоремасын қолдануға болады. Сонда
оқиғалары да қос-қостан үйлесімсіз. Олай болса, бұл оқиғаларға қосу теоремасын қолдануға болады. Сонда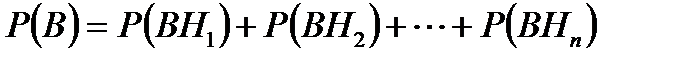 шығады.
шығады. болады.
болады.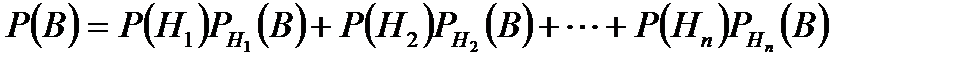
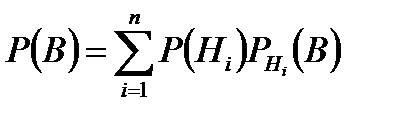
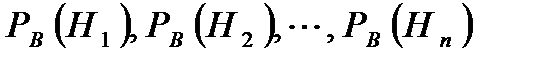 ықтималдықтар мәнін анықтауға тіреледі. Бұл ықтималдықты анықтау үшін, көбейту теоремасы мен ықтималдықтардың толық формуласын пайдаланамыз.
ықтималдықтар мәнін анықтауға тіреледі. Бұл ықтималдықты анықтау үшін, көбейту теоремасы мен ықтималдықтардың толық формуласын пайдаланамыз.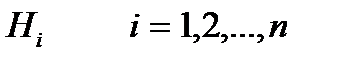 үшін
үшін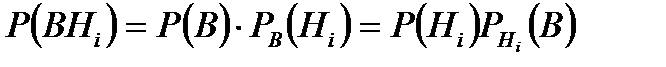
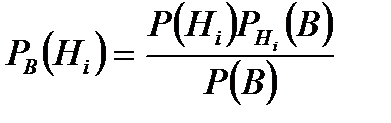
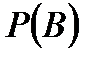 мәнін қойсақ, онда
мәнін қойсақ, онда 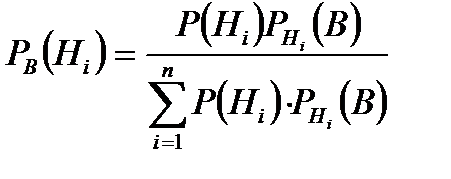
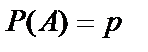 болсын. Онда А оқиғасының пайда болмауы
болсын. Онда А оқиғасының пайда болмауы 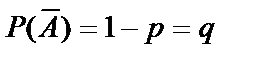 болады. Енді осы тәжірибелер нәтижесінде А оқиғасы k рет пайда болу ықтималдығын
болады. Енді осы тәжірибелер нәтижесінде А оқиғасы k рет пайда болу ықтималдығын 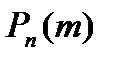 деп белгілейді және ол мынаған тең:
деп белгілейді және ол мынаған тең: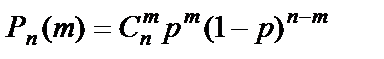
 шартын қанағаттандыратын барлық к-лар үшін бірқалыпты түрде
шартын қанағаттандыратын барлық к-лар үшін бірқалыпты түрде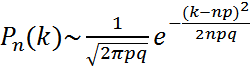 , n
, n 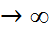
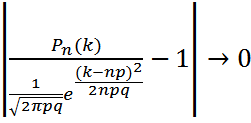
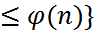
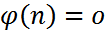 ((npq
((npq 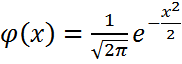
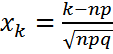 белгілеуін енгізсек, онда теореманы былай тұжырымдауға болады.
белгілеуін енгізсек, онда теореманы былай тұжырымдауға болады.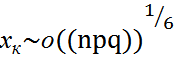 үшін
үшін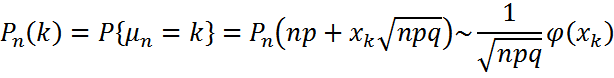
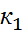 мен
мен 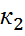 арасында болу ықтималдығы Pn(k1,k2) жуық шамамен мынаған тең:
арасында болу ықтималдығы Pn(k1,k2) жуық шамамен мынаған тең: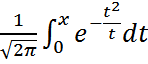 және
және 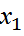 =
= 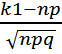 x2=
x2= 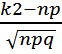
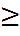 20 болған кезде қолданған жөн. Есептеуді оңайлату үшін ықтималдылықтар теориясы оқулықтарында Ф(х)=
20 болған кезде қолданған жөн. Есептеуді оңайлату үшін ықтималдылықтар теориясы оқулықтарында Ф(х)= 


