Кездейсоқ оқиғалар. Ықтималдықтың анықтамалары. Ықтималдықтарды қосу және көбейту теоремалары.
17.Кездейсоқ оқиғалар. Ықтималдықтың анықтамалары. Ықтималдықтарды қосу және көбейту теоремалары.
А оқиғасының пайда болу мүмкіндігінің сандық мөлшеріне р(А) функциясының мәні алынады. Мұны осы А оқиғасының ықтималдығы деп атайды.Ықтималдықтың классикалық анықтамасы оқиғалардың тең мүмкіндіктеріне (тең ықтималдығына) сүйенеді.А оқиғасы қолайлы жағдайлар санының (т) сынаудың тең мүмкіндікті барлық жағдайлар санын (п) қатынасын А оқиғасының ықтималдығы деп атайды және былай жазады:
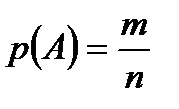
Ықтималдықтың бұл анықтамасын классикалық анықтама дейміз.
Күрделі оқиға ықтималдығын анықтау үшін негізінен ықтималдықтарды қосу және көбейту теоремаларын пайдаланады.
Қосу теоремасы. Үйлесімсіз А және В оқиғаларының қосындысының ықтималдығы олардың ықтималдықтардың қосындысына тең, яғни
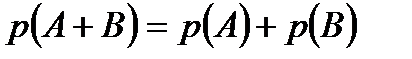
Д/уі: Теореманы дәлелдеу үшін (1) теңдіктегі үш ықтималдықты есептеп, ол мәндерді (1) теңдікке қойып, оның дұрыстығына көз жеткізу жеткілікті.
Қосудың кеңейтілген теоремасы
Егер А1, А2, ...,Ап қос-қостан үйлесімсіз оқиғалар болса 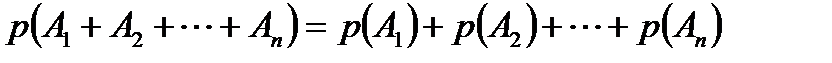
1-салдар.қос-қостан үйлесімсіз сынау нәтижелері ықтималдықтарының қосындысы бірге тең.
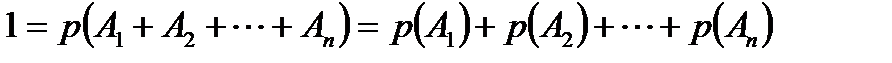 2-салдар Қарама-қарсы екі оқиға ықтималдықтарының қосындысы бірге тең, яғни 2-салдар Қарама-қарсы екі оқиға ықтималдықтарының қосындысы бірге тең, яғни
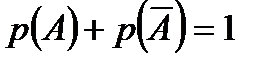
a)Ықтималдықтарды көбейту теоремасы
Екі тәуелді оқиға көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығын сол оқиға пайда болды деп алынғандағы екінші оқиғаның шартты ықтималдығына көбейткенге тең:
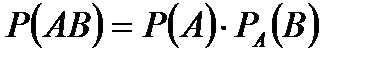
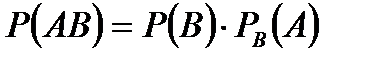
Теорема. Екі тәуелсіз оқиғалар көбейтіндісінің ықтималдығы олардың шартсыз ықтималдықтарының көбейтіндісіне тең, яғни
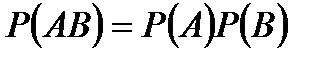 болады. болады.
|