
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
y’’=f(x), y’’=f(x,y’), y’’=f(y,y’) түріндегі дифференциалдық теңдеулерді шешудің әдістері.Содержание книги
Поиск на нашем сайте
3.y’’=f(x), y’’=f(x,y’), y’’=f(y,y’) түріндегі дифференциалдық теңдеулерді шешудің әдістері. 1) Квадратура әдісі. y’=ʃf(x)dx+c1 y(x)=ʃ(ʃf(x)dx)dx+c1x+c2 ʃf(x)dx=φ(x) 2) y’’=f(x,y’), y’=p, y’’=p’алмастыру арқылы p’=f(x,p)немесе F(x,p,p’)=0 бірінші ретті теңдеуге келтіріледі. 3) Тәуелсіз айнымал айқын түрде кірмейтін F(y,y’,…,y(n))=0 теңдеуі y’=p(y) алмастыру арқылы реті бірге төмендетілген теңдеуге келеді. Бұл алмастыру үшін y’’==p,
10. Екінші ретті тұрақты коэффицентті, сызықты, біртекті дифференциялдық теңдеулер. Екінші ретті коэффиценттері тұрақты біртекті жәй сызықтық дифференциялдық теңдеуді қарастырайық: a0y’’+a1y’+a2y=0 (1) теңдеуі берілсін дейік, мұндағы а0, а1, а2 коэффиценттері тұрақты сандар. Бұл теңдеудің дербес шешімін y(x)=ekx түрінде іздеп көрейік, мұнд. K- анықтауға жататын белгісіз. (1)- теңдеудің сол жағына y(x)=ekx, y’(x)=ekx , y’’(x)=ekx өрнектерін қойып, мына теңдеуді шығарып аламыз. (a0k2+a1k+a2) ekx=0. ekx функциясы х-тің ешбір мәнінде нөлге тең болмайтындықтан y(x)=ekx функциясы (1)-теңдеудің шешімі болуы үшін a0k2+a1k+a2 үшмүшелігі нөлге тең болуы қажетті және жеткілікті. a0k2+a1k+a2 үшмүшелігі характеристикалық үшмүшелік, ал a0k2+a1k+a2=0 теңдеуі(1)-дифференциялдық теңдеудің характеристикалық теңдеуі деп аталады. Характеристикалық үшмүшелікті қарастырғанда әртүрлі жағдайларға кездесеміз. 1-жағдай. Сипаттамалық үшмүшліктің әртүрлі нақты екі түбірі бар дейік, оларды k1 және k2 арқылы белгілейік және k1¹k2 сонда біз (1)- теңдеудің әртүрлі дербес екі шешімін : у1(x)=ek1x және у2(x)=ek2x шығарып аламыз. Бұл дербес екі шешім бір-бірімен бірі сызықтық байланыссыз, барлық сан өсінде негіздік дербес шешімдер жүйесін құрып, Вронскийдің анықтауышы деп аталатын екі ретті анықтауышты береді: w(x)= Демек (1)-теңдеудің жалпы шешімі мына түрде жазылады: y (x)= C1×ek1x+C2× ek2x. 2-жағдай. Енді сипаттамалық үшмүшеліктің бір-біріне тең нақты екі түбірі бар болсын. Бұл жағдайда a0k2+a1k+a2 квадрат үшмүшеліктің дискриминанты нөлге тең. Сондықтан K1=k2=k0= Бұл жағдайда сипаттамалық теңдеудің нақты бір шешімін у1(x)=ek0x бірден жазып аламыз. Ал, екінші дербес шешімді бірінші дербес шешімнен сызықтық тәуелсіз етіп, у2(x)=х×ek2x түрінде таңдап аламыз. Сонда сипаттамалық үшмүшелікке сәйкес (1)- теңдеудің жалпы шешімі былай жазылады: y (x)= C1×ek0x+C2×х ek0x =(C1+C2x) ek0x. 3-жағдай. Егерде сипаттамалық үшмүшеліктің түбірлері комплекс сандар болса, k1=a+ib ; k2=a-ib, онда (1)-теңдеудің жалпы шешімі былай жазылады: 1-Мысал: 1)y’’-5y’+6y=0 теңдеуін алып қарастырайық. Бұл теңдеудің сипаттамалық үшмүшелігінің k2-5k+6 түбірлері k1=2; k2=3. Сондықтан сипаттамалық теңдеудің негіздік дербес шешімдер жүйесі: у1(x)=e2x және у2(x)=e3x шешімдерінен тұрады. Демек біртекті екінші ретті дифференциялдық теңдеудің жалпы шешімі: y (x)= C1×e2x+C2× e3x болады. 2-Мысал. y’’+6y’+13y=0 дифференциалдық теңдеудің жалпы шешімін табу керек. Шешуі. Берілген теңдеудің k2-2k+1=0 сипаттаушы теңдеуінің k=-3
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.237.218 (0.006 с.) |

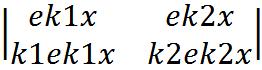 =(k2-k1)×e(k1+k2)x¹0.
=(k2-k1)×e(k1+k2)x¹0.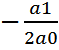
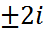 түбірлері комплекс түйіндес сандар. Теңдеудің сызықтық тәуелсіз шешімдері y1=e-3xcos2x, y2=e-3xsin2x фуекциялар болып, оның жалпы шешімі y=e-3x(C1cos2x+C2sin2x) болады.
түбірлері комплекс түйіндес сандар. Теңдеудің сызықтық тәуелсіз шешімдері y1=e-3xcos2x, y2=e-3xsin2x фуекциялар болып, оның жалпы шешімі y=e-3x(C1cos2x+C2sin2x) болады.


