Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
а)Кездейсоқ шамалардың берілген аралықта мен қабылдау ықтималдығы.Содержание книги
Поиск на нашем сайте
1.Берілген интервал бойынша үздіксіз кездейсоқ шаманың мән қабылдау ықтималдығы. Теорема. Х үздіксіз кездейсоқ шамасы (а,b) интервалында мән қабылдаса, онда үлестіру тығыздығының а-дан b-ға дейінгі анықталған интегралына тең
Дәлелдеуі.P(a ≤ x < b)=F(b) – F(a) теңдігін пайдаланамыз. Ньютон-Лейбниц формуласы бойынша P(a ≤ X < b)= Ал P(a ≤ x < b)=
2.Көрсеткішті үлестірудің берілген интервалдан мән қабылдау ықтималдығы. Х үздіксіз кездейсоқ шаманың (а,b) интервалдан мән қабылдау ықтималдығын берілген үлестіру бойынша табамыз
Ол үшін мына формуланы пайдаланамыз P(a < X < b)=F(b) – F(a). Мұнда P(a < X <b) = e-λa – e-λb. 3.Қалыпты кездейсоқ шаманың берілген интервалдан мән қабылдау ықтималдығы. Теорема.Қалыпты заңымен үлестірілген кездейсоқ шаманың (α,β) интервалында болу ықтималдығы мына формуламен анықталады: P(α < х <β)= Дәлелдеуі.Қалыпты үлестіру заңы бойынша (α,β) интервалында мән қабылдау ықтималдығы мынаған тең: P(α < х <β)= Егер x=α, онда P(α ≤ х <β)= Лаплас функциясы бойынша Φ(x)= P(α < х <β)= в)Анықтама. Егер Х кездейсоқ шамасының үлестірім тығыздығы
теңдігі арқылы анықталса, онда Х кездейсоқ шамасы көрсеткіштік үлестірім заңымен берілген деп атайды. Үлестірім функциясын табатын болсақ
Енді математикалық үмітін есептейік:
U=x, du=dx =
Дисперсияны есептеу үшін M(x2) мәнін табамыз
Дисперсияның мәнін Д(х)=М(х2)-М2(х) формуласымен есептесек
Бұдан көрсеткіштік үлестірім заңы үшін
с) Анықтама. Егер үздіксіз кездейсоқ шама мына үлестіру тығыздығы
арқылы берілсе, онда ол қалыпты үлестіру заңыменберілген дейді. Қалыпты үлестіру екі параметр арқылы анықталатынын көреміз:
a және σ Бұл параметрлердің мағынасы мынадай: а) а – математикалық үмітке тең, яғни M(x)=a б) σ – қалыпты үлестіруі орташа квадраттық ауытқуына тең σ(х)=σ. Енді осыларды дәлелдейік. а) Үздіксіз кездейсоқ шаманың математикалық үмітінің анықтамасы бойынша
Жаңа айнымалы енгізейік:
Қалыпты үлестірудің математикалық үміті а параметріне тең: М(х)=а. б) Үздіксіз кездейсоқ шама дисперсиясының анықтамасы бойынша
М(х)=а екені белгілі. Жаңа айнымалы енгізейік:
Интегралды табамызда ν=z, dν=
|
|||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.174.5 (0.009 с.) |

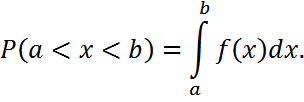
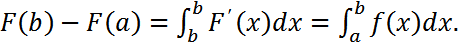
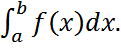
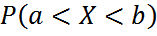 болғандықтан мына теңдікті аламыз
болғандықтан мына теңдікті аламыз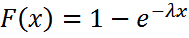 (x ≥ 0)
(x ≥ 0)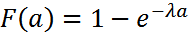 ,
, 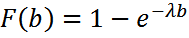 екенін ескеріп, кездейсоқ шаманың (а,b) интервалдан мән қабылдау ықтималдығын аламыз:
екенін ескеріп, кездейсоқ шаманың (а,b) интервалдан мән қабылдау ықтималдығын аламыз: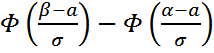 (*)
(*)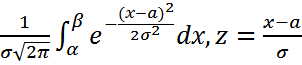 десек, осыдан x= σz+a; dx=σdz.
десек, осыдан x= σz+a; dx=σdz.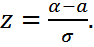 Егер x=β, онда
Егер x=β, онда 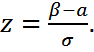
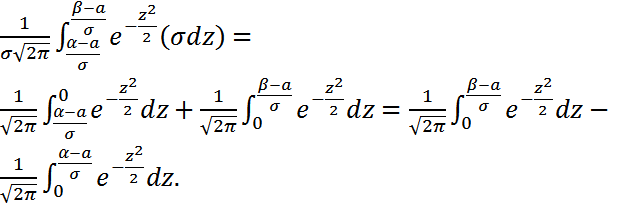
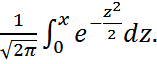 Сонда
Сонда
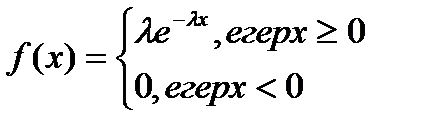
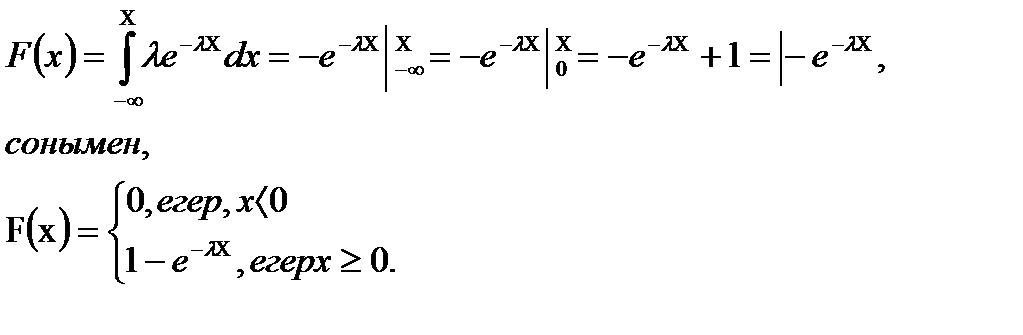
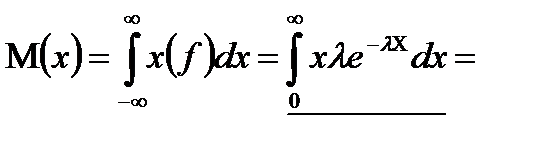 бөліктеп интегралдаймыз
бөліктеп интегралдаймыз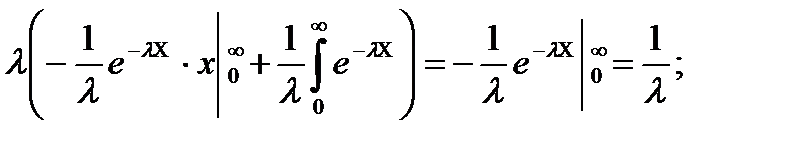
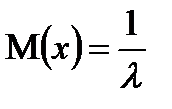
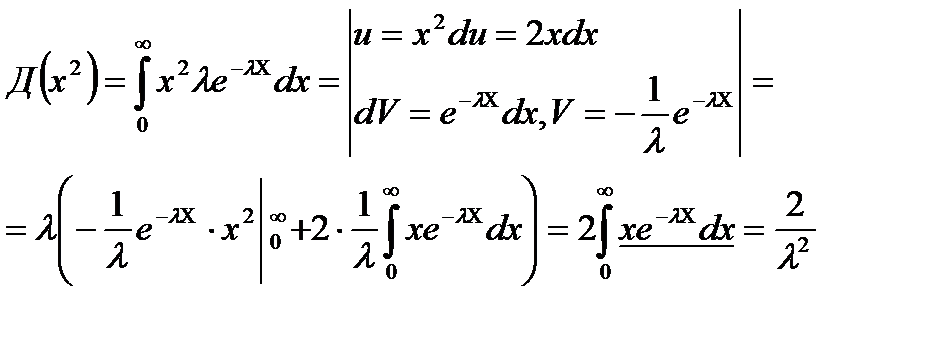
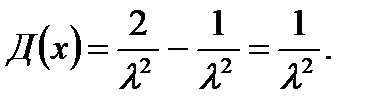
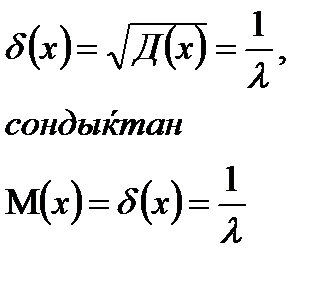
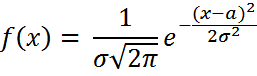
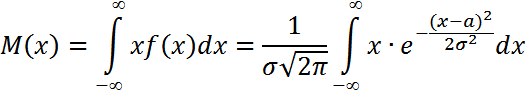
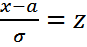 . Осыдан x=σz+a, dx=σdz.
. Осыдан x=σz+a, dx=σdz.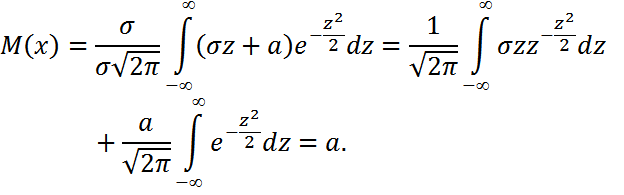
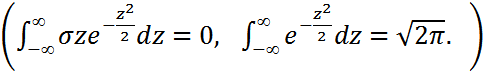 - бұл Пуассон интегралы бойынша.
- бұл Пуассон интегралы бойынша.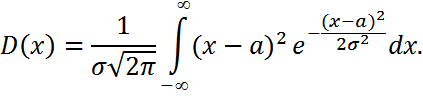
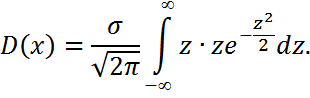
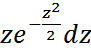 қойсақ, онда табамызD(x)=σ2, σ(x)=
қойсақ, онда табамызD(x)=σ2, σ(x)=