
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые случайные процессы.Содержание книги
Поиск на нашем сайте Процессы массового обслуживания.К числу случайных процессов, изучаемых методом имитационного моделирования относятся, в частности, процессы, связанные с формированием и обслуживанием очередей. Простейшая задача данного класса такова. Имеется система массового обслуживания с одним узлом обслуживания (магазин с одним продавцом, ремонтная зона в автохозяйстве, травмпункт с одним врачом, телефонная станция с одним входом, сервер с одним входным каналом и т.д.). К услугам системы клиенты прибегают случайным образом (с заданной функцией распределения отрезков времени между приходами). Если система свободна, то начинает обслуживать клиента сразу, иначе ставит его в очередь. Длительность обслуживания каждого клиента — случайная величина с известным законом распределения. В ходе решения данной задачи требуется дать ответ на вопросы типа: какова функция распределения вероятностей времени ожидания клиента в очереди? Времени простоя системы в ожидании клиентов? Если сами эти функции определять сложно, то каковы их наиболее важные характеристики (т.е. математическое ожидание, дисперсия и т.д.)? Задача Бюффона. Французский натуралист, биолог, математик, естествоиспытатель и писатель XVIII века Жорж-Луи Леклерк де Бюффон аналитически нашел, что если на поле, разграфленное параллельными прямыми, расстояние между которыми L, бросается наугад игла длиной l, то вероятность того, что игла пересечет хотя бы одну прямую, определяется формулой «Бросок иглы» моделируется генерированием трех случайных чисел – координат одного из концов иглы X,Y и угла наклона иглы к положительному направлению оси абсцисс α. Координаты второго конца иглы вычисляются из прямоугольного треугольника с гипотенузой l и острым углом α (или π-α). Для простоты можно считать, что прямые проведены через точки 0, 1, 2, … Тогда условием пересечения иглой какой-либо прямой будет неравенство целых частей ординат концов иглы. Процесс случайного одномерного блуждания (модель «пьяницы»). В начальный момент времени точка находится на нулевой отметке числовой прямой. Блуждание задается по правилу: если случайное число из отрезка [0,1] меньше 0,5, то делается шаг вправо на расстояние h, в противном случае ¾ влево. Распределение случайных чисел принимается равновероятным. Обычно ставятся следующий вопрос: какова вероятность удаления точки на расстояние k от начального положения через n шагов. Обобщение данной модели на плоскость и на большое количество точек позволяет моделировать процессы, происходящие в жидкостях и газах.
|
||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 39; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

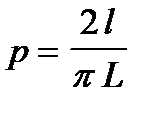 . Эта задача дала способ имитационному определению числа p. Действительно, если L=2l, то
. Эта задача дала способ имитационному определению числа p. Действительно, если L=2l, то 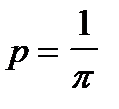 .
.


