
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пример выполнения задания. Задание к лабораторной работеСодержание книги
Поиск на нашем сайте
Пример выполнения задания Задача.Реализовать моделирование межвидовой конкуренции при фиксированных значениях начальной численности популяций В качестве математической модели межвидовой конкуренции примем формулы (3). Исследуем модель путем нахождения особых точек на фазовой плоскости (N1ON2) ([6]). Как известно, судьбы популяций зависят от соотношения параметров r1, r2, β1, β2, α1, α2, а именно, обе популяции выживают, если на фазовой плоскости существует особая точка- устойчивый узел- c координатами
1. Выписать математическую модель, определить состав набора входных параметров и их конкретные числовые значения. 2. Спроектировать таблицу для представления результатов моделирования, предусмотрев в ней области ввода исходных данных, параметров модели и вывода результатов. 3. Выбрать метод интегрирования дифференциальных уравнений модели, разработать самостоятельно табличный алгоритм интегрирования с заданной точностью. 4. Произвести отладку и тестирование алгоритма в среде табличного процессора. 5. Выполнить конкретное задание из своего варианта работы. 6. Качественно проанализировать результаты моделирования. 7. Создать текстовый отчет по лабораторной работе, включающий: - постановку задачи и описание модели; - результаты тестирования программы; - результаты, полученные в ходе выполнения задания (в различных формах); - качественный анализ результатов.
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 4; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.194.30 (0.005 с.) |

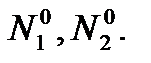 Проанализировать зависимость судьбы популяций от соотношения значений параметров r1, r2, β1, β2, α1, α2.Выяснить, при каких условиях обе популяции выживают.
Проанализировать зависимость судьбы популяций от соотношения значений параметров r1, r2, β1, β2, α1, α2.Выяснить, при каких условиях обе популяции выживают.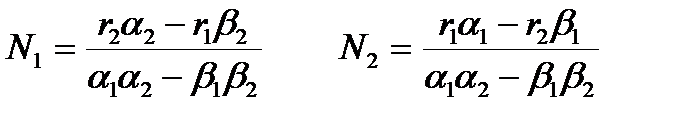 . При этом выполняются следующие соотношения:
. При этом выполняются следующие соотношения: 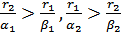 . Выберем значения параметров r1, r2, α1, α2 произвольно (имея в виду, что r1, r2 – это числа, означающие скорость роста популяции в отсутствие конкуренции и должны иметь значения, большие единицы, а α1, α2 характеризуют конкуренцию, т.е. вероятность гибели особи при встрече с другой особью и должны быть меньше единицы), а параметры β1, β2 получим из соотношений
. Выберем значения параметров r1, r2, α1, α2 произвольно (имея в виду, что r1, r2 – это числа, означающие скорость роста популяции в отсутствие конкуренции и должны иметь значения, большие единицы, а α1, α2 характеризуют конкуренцию, т.е. вероятность гибели особи при встрече с другой особью и должны быть меньше единицы), а параметры β1, β2 получим из соотношений 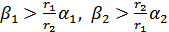 . Начальные значения численности популяций
. Начальные значения численности популяций 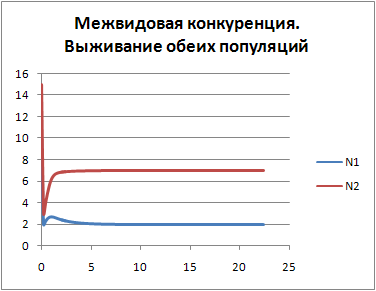
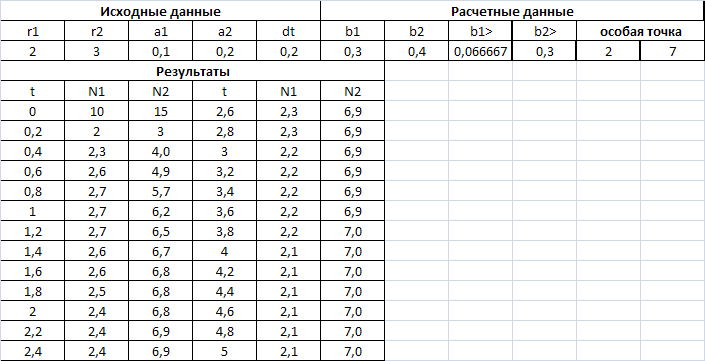 Рис.1 При заданных значения входных параметров обе популяции выживают
Рис.1 При заданных значения входных параметров обе популяции выживают


