
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитті материалдардың анизотропиясы менСодержание книги
Поиск на нашем сайте
2.24 Магнитті материалдардың анизотропиясы мен магнитострикциясы Магнитті материалдардан өндіріс пен тұрмысқа қажетті материалдар дайындаған уақытта олардың магнитті анизотропиялық қасиеті мен магнитострикциялық (магнитті материалдарды магнит өрісіне енгізген уақытта оның сызықты өлшемдерінің өзгеру қасиеті) қасиеттерін ескермеуге болмайды. Жоғарыда келтірілген алмасу энергиясы материалдың барлық жағында бірдей шамаға ие болатындықтан ол изо- тропты (барлық жағында бірдей) қасиетке ие болады. Ол магнит моменттерін реттелген күйге келтіргенімен домендердің қорытқы магнит моментінің бағытын кристаллографилық остің бағытына қарай бағыттай алмайды. Магнитті материалдарда кейбір кристаллографиялық остердің бойында жеңіл, өте жеңіл, ауыр магниттелу құбылыстары байқалады. Осындай бағыттарға көлемге ортақталған кристалдық торға ие болатын темірдің жеке кристалында Магнитті кристаллографиялық анизотропияның энер- гиясын магниттелу векторының
мұндағы Осы тұрақтылардың таңбасы мен шамасына байланысты қандай бағыттың жеңіл, ауыр т.б.с.с. магниттелуге сәйкес келетіндігін анықтауға болады. Магнитті материалды екі полюстан тұратын кішкентай магнитшелерден тұрады деп жорысақ, онда магнит анизотропия энергиясының пайда болуына магниттік диполь-дипольдік өзара әсерлесу жауапты болып табылады. Жоғарыда келтірілген изотроптық алмасу энергиясы тек атомның орбиталық магнит моменті нөлге тең болғанда ғана жүзеге асырылады. Егер атомның орбиталық магнит моменті Атомды қоршаға электр өрісі (кристалдық тордық өрісі) электронның орбиталық қозғалысына әсер етеді. Сондықтан кристалдық тордың өрісі, электрон орбитасын белгілі бір кристаллографиялық өстің бойына қарай бұруға тырысады. Атомның спин-орбиталық моменті кристалл өрісімен өзара әсерге түсіп, келтірілген байланыс арқылы электронның спиндік қозғалысына да өз әсерін тигізеді. Анизотропияның осындай "механизмін" жеке ионды анизотропия деп атайды. Өйткені ол жеке ионның орбиталық моментінің кристалдың барлық өрісімен байланысын береді. Бұл жерде мынадай екі жағыдайда еске алуға тура келеді. Егер орбиталық моменттің кристалл өрісімен өзара әсерлесу энергиясының (
2.20-сурет.Магнит анизотропия энергиясы а-куб кристалдық торының негізгі бағыттары, б-темір монокристалының негізгі кристаллографиялық бағыттары бойынша магниттелінуі, в, г-Жеке ионды анизотропияның сұлбасы (в-3d металдар, 2 сирек кездесетін металдар үшін) "–" берік байланыс "~" әлсіз байланысты көрсетеді Осындай магнитті материалға сырттан магнит өрісінің тудыратын болса, орбиталық магнит моментіне қатысты спиндік магнит моментінің бағыты өзгереді. Бұл жағыдайда магнит анизотропия энергиясының өзгерісіне спин-орбиталық әсерлесу жауапты (2.20в- сурет) болады. Сирек кездесетін элементтерде жеке иондық ани-зотропия жүзеге асады. Бұл магнитті материалдарда спин-орбиталық өзара әсерлесу энергиясы, орбиталық моменттің кристалл өрісімен әсерлесу энергиясынан көп болады. Сондықтан осындай магнитті материалдарға сырттан магнит өрісін тудырған кезде орбиталық және спиндік магнит моменттері тұтас бірге (2.20,г- сурет) бұрылады. Көпшілік қолды техникалық магнитті материалдарда анизотропияның жеке ионды табиғаты пайдаланылады: а) куб кристалдық торының негізгі бағыттары; б) темір монокристалының негізгі кристаллографиялық бағыттары бойынша магниттелінуі; в, г) жеке ионды анизотропияның сұлбасы (-3d металдар, 2 сирек кездесетін металдар үшін) "–" берік байланыс "~" әлсіз байланысты көрсетеді Магниттті материалдарды қолданғанда ерекше ескеретін тағы да бір қасиеті – магнитострикция. Ферромагнитті материа-лдарға сырттан магнит өрісін туғызғанда біздің еркімізден тыс сызықтық өлшемдерінің өзгеруі Магнит өрісіндегі магнитті материалдардың сызықтық өлшемдерінің өзгерісін олардың сыртқы күштің әсерінен болатын механикалық деформациясымен салыстыруға болады. Механикалық деформация кезінде атомдардың арақашықтығы өзгереді. Қорытындысында атомдардың электрондық қабаттары бірін-бірі жабады. Бұл магниттік анизотропия энергиясының өзгерісіне әкеліп соғады. Сондықтан магнитті материалдардың магниттелуі бағытын өзгертетін болсақ, онда ол оның кристалдық торын деформацияға ұшыратады. Магнитті материал үшін алмасу энергиясы мен магнит анизотропия энергиясы қосындысының ең төменгі мәнге ие болуы оның пішінін сақтау үшін тиімді болып табылады. Егер алмасу энергиясы изотропты болып, кристалдың магниттелуі кристаллографиялық оське тәуелсіз болса, онда пайда болатын магнитострикция да изотропты болады. Бұл магнитостиркцияны алмасу магнитострикциясы немесе пара-процесстің магнитострикциясы деп атайды. Магнитті материалдарда кездесетін алмасу маг-нитострикциясының шамасы үлкен шамаға ие болмайды. Оған қарама-қарсы магнитті анизотропия энергиясына байланысты кристалда пайда болатын анизотропиялық магни- тострикцияның шамасы ескерерліктей мәнге ие болады. Мысалы, куб кристалында оның мәні кристаллографиялық ось бағыттарында әртүрлі мәнге ие болады.
мұндағы –
Егер Онда салыстырмалы деформация
мұндағы Магнитострикциялық деформацияның пайда болуын мынадай сұлбаның көмегі арқылы түсіндіруге (2.22- сурет) болады: а) кюри б) в) сыртқы магнит өрісі г) магнит өрісінің үлгінің магнитострикциялық дефор -мациясына әсері. Кюри температурасынан жоғары Магниттелу векторын Көп доменді кристалдарды сыртқы магнит өрісіне енгізгенде, қосымша магнитострикциялық деформация пайда болады. Өйткені көп домендер сыртқы магнит өрісінде жеке доменге көшуге тырысады. Магнитострикциялық деформа-цияның шамасы салыстырмалы деформация шамасымен Ауыспалы валентті 3d металлдар үшін магнито- стрикциялық деформация
в г 2.21-сурет.Магнитострикциялық деформацияның пайда болуы а-шар формалы. б-өзінің өлшемін ұлғайтуы, в-эллипс формалы, г-эллипсоиданың осінің бағытына бағыттас Ферромагнетиктердегі магнитострикция құбылысына көп тоқталу себебімізді айта кеткен жөн. Өйткені магнито-стрикциялық құбылыс техникада ультрадыбыс алудың бірден-бір көзі болып табылады. Қазіргі техника мен ғылым өркендеген кезде ультрадыбыстың қолдану аясы күннен күнге кеңейіп келеді.
2.25. Магнетиктердің термодинамикасы. Магниттеу жұмысы. Магниттердің жалпы термодинамикалық қатынасы. Тұрақты қысымдағы және тұрақты көлемдегі магниттердің меншікті жылу сыйымдылықтары. Магнитколориметрлік құбылыс. Екі А және Б магниттерді әртүрлі полюстері арқылы бір- бірімен беттескен (
2.22-сурет. А және Б екі тұрақты магниттердің магниттелуінің өріспен өзара әсерлесуі
Мұндағы S- магниттердің полюстерінің көлденең қима- сының ауданы. Оларды бір- бірінен
Магнит зарядының беттік тығыздығы
Магнит моменттерінің бір өлшем көлемге қатынасын магниттелу пәрменділігі немесе көлемдік магниттелу деп атайды. Тәжірибеде А магниттің магниттелуі Б магниттің өрісінде немесе керісінше іске асады. Сонда сыртқы күшке қарсы атқарылған жұмыс W-ның көлемге
Мұндағы «-» таңбасы жұмыс жүйе үстінен жүргізіледі дегенді білдіреді. Егер І магниттелу Н магнит өрісінде біртекті болмаса, онда
Немесе интеграл түрінде
Егер
Мұндағы
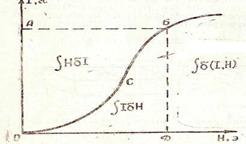
магниттелудің сыртқы жұмысы деп аталады. Оны сүлбе 2.23- сурет түрінде көрсетуге болады. Сонда ОАВСО- қисықтың ауданы жұмсалған жұмыс, ал магнитті магниттеуге кеткен жұмыс ОСВDO ауданымен өлшенеді.
2.23- сурет. Магниттеу жұмысын кескіндеу сүлбесі
Магнитті сыртқы Н магнит өрісіне енгізген кезде реалаксация уақытынан кейін оның күйі өзгереді де жаңа термодинамикалық күйге өтеді. Термодинамикалық қатынасты оқып үйренуді жеңілдету мақсатында біз тек қайтымды процесстерді ғана қарастырамыз. Яғни гитерезис құблысын еске алмаймыз. Осы жағыдай үшін макроскопиялық термодинамикалық процесстерді қарас-тырайық. Термодинамиканың бірінші заңынан жүйеге берілген Егер ішкі энергия магнитті магниттеуге және қыздыруға жұмсалса, онда қайтымды процесстердің энтро пиясы
Ал магнитті магниттеуге жұмсалған жұмыс
Егер магниттелу мен магниттің көлемі бір мезгілде өз- герсе, онда жұмыс
мұндағы Р- қысым, еркін энергия
F=U-TS (2.77)
Термодинамикалық потенциал
Ф=F+PV=U-TS+PV (2.78)
Мұндағы Т температура. Біз магниттер үшін термодинамикалық потенциалды басқадай формада жаза аламыз.
Ф=F+PV-IH (2.79)
Мұндағы IH магнитті магниттеудің сыртқы энергиясы, Енді (2.74) (2.76) теңдеулерді
Егер (2.77) теңдеуді дифференциалдап (2.80) теңдеуді ескере отырып
Енді Ф термодинамикалық потенциалды дифференциалдап (2.82) теңдеуді ескерсек
Магниттердің негізгі термодинамикалық теңдеулерін Гиббстің кез келген термодинамикалық функциясынан (U,F,Ф) шығарып алуға болады. Жоғарыдағы термодинамикалық потенциалдағы
Сонда
Осы теңдеуден
(а)- (ж) (2.84) белгілеулерді пайдалана отырып, магниттер термодинамикасынын дифференциалдық теңдеулерін мынадай түрде жазамыз.
Мұндағы индекстер (Н,Т,Р) қайсысының тұрақты бола- тының көрсетеді. Мысал ретінде магниттердің жылу сы -йымдылығын қарастырайық. Жылу сыйымдылық дегеніміз берілген жылу мөлше- рінің қандай да бір процесс кезінде температураны жоғарылатқан кезде жұмсалатын жылу мөлшері. Магниттердің жылу сыйымдылығы қысымға (Р), көлемге (V) магниттелуге (І), магнит өрісінің кернеуіне (Н) тәуелді болады. Сонымен магниттердің жылу сыйымдылығы Н:
Мұндағы x,y параметрлері меншікті жылу сыйымдылықтың өзгеру кезінде тұрақты болады. Термодинамиканың екінші бастамасын
Меншікті жылу сыйымдылықтың анықтамасы бойынша
Егер айнымалылар Т,Р,Н алатын болсақ онда энтропияның дифференциалы үшін
Енді жаңа айнымалы Т,Р,І қарастырайық.
Осы (2.93) теңдеу мен (2.92) теңдеулерін біріктіре отырып
Егер Р,І=const болса, онда
Осы теңдеуді Т көбейтіп және (2.91) теңдеуді ескере отырып,
Тағы да (2.87) теңдеуді пайдалана отырып магниттердің термодинамикалық теңдеулерінен
түрінде де жазуға болады. Бұл термодинамикалық теңдеулер Магниттердегі магнит өрісін адиабаталық түрде өзгерткенде температурасының өзгерісін магнитокалариметрлік эффект деп атайды. Адиабаталық түрде
Ол өз кезегінде магниттің температурасының өзгеруіне әкеледі. Сыртқы магнит өрісінің кернеуін арттырған кезде І магниттелу векторы өседі. Яғни магниттің ішкі энергиясы азайған кезде магниттелу шамасына жауапты элементар магнит моменттерінің саны өсетін сияқты болып көрінеді. Бұл жағыдайда магнит энергиясы магниттелу жұмысына тең шамаға
немесе
Егер тәуелсіз айнымалы ретінде Т мен І алатын болсақ, онда
Енді (2.99)(2.98) теңдеулерден
немесе
Адиабаталық процесс жағыдайында
Сонда магниттің тұрақты V көлеммен І магниттелу кезіндегі меншікті жылу сыйымдылығы
Осы (2.102) теңдеуді (2.100) қойып
Немесе (2.104) (2.98) теңдеулерден
Енді
Сонымен (2.103) (2.106) теңдеулер магниттер үшін магнитокалориметрлік эффектінің өрнектерін береді. Келесі мысал ретінде магниттердегі магнитострикция құбылысын қарастыруға болады. Егер (2.83) теңдеудегі көлемнің орнына
Бұл теңдеуден T,P және T,H тұрақтылар ретінде алып мынадай теңдеулер жазуға болады.
Осы теңдеулерден екінші ретті туынды алсақ
Енді
Бұл (2.108) және (2.109) теңдеулер магнитострикция мен магнит өрісінің кернеулігі арасындағы кері пропор -ционалдықты береді. Кез келген магнитті магнит өрісіне орналастырғанда ол деформацияланады. Деформацияланған магниттің магниттік қасиеттерін сипаттайтын статистикалық және динамикалық қасиеттері өзгереді. Ферромагниттердегі магнитострикция құбылысы олардың серпімді қаттылық коэффициентінің төмендеуін туғызады. Кез келген магнитострикция коэффициенті ферромагнетиктердегі тосын магниттелу векторының бұрылуын өзгертеді. Магнитострикция кезінде Егер кезкелген ферромагнитті денеде Магниттік жылулық құбылыстардың ішінде өндірістье қолданылатындардың бір ретінде магниттерді адиабаталық магнитсіздендіруді қолдану болып табылады. Бұл құбылыс өте төменгі температура алу үшін қолданылады. Магниттерге өте үлкен магнит өрісін түсірген кезде спиндердің жылулық тербелістері азаяды. Енді осы магнит өрісін алып тастайтын болсақ, онда спиндердің ретсізденуі жүреді де магниттің температурасы төмендейді. Егер спиндер жүйесі оқшауланған болса, онда энтропия өз шамасын сақтап, сыртқы магнит өрісін қосқан кезде спиндер өздерінің реттелген күйін сақтайды да магниттердің температурасының төмендеуіне әкеледі. Осы физикалық құбылыстар төменгі температура алудың физикалық негізі болып табылады.
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.181.90 (0.014 с.) |

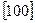 жеңіл,
жеңіл, 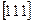 ауыр магниттелу бағытына сәйкес (2.20,б- сурет) келеді. Осыдан барып кристаллографиялық магниттік анизотропия энергиясы деген ұғым келіп шығады. Магниттік анизотропияның өлшемі ретінде магниттелу век- торын жеңіл магниттелу бағытынан ауыр магниттелу бағытына бұруға жұмсалатын энергия мөлшері алынады. Осы энергия көптеген техникада қолданылатын ферромагнетиктердің қаси-етін анықтайды.
ауыр магниттелу бағытына сәйкес (2.20,б- сурет) келеді. Осыдан барып кристаллографиялық магниттік анизотропия энергиясы деген ұғым келіп шығады. Магниттік анизотропияның өлшемі ретінде магниттелу век- торын жеңіл магниттелу бағытынан ауыр магниттелу бағытына бұруға жұмсалатын энергия мөлшері алынады. Осы энергия көптеген техникада қолданылатын ферромагнетиктердің қаси-етін анықтайды.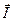 кристаллографиялық осьте-рімен жасайтын бұрыштары арқылы
кристаллографиялық осьте-рімен жасайтын бұрыштары арқылы 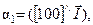
 белгілейді. Сонда анизотропия энергиясы куб кристалдары үшін
белгілейді. Сонда анизотропия энергиясы куб кристалдары үшін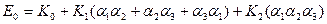 (1.67)
(1.67)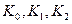 –анизотропия тұрақтылары;
–анизотропия тұрақтылары; 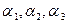 - ба-ғыттауыш косинустары деп аталады.
- ба-ғыттауыш косинустары деп аталады.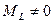 нөлден өзгеше мәнге ие болса, онда қосымша анизотропиялық энергия шамасы пайда болады. Осы уақытта электронның ядроны айнала қозғалатын тұйық орбитасы деформацияланып, шеңбер орнына элипс формасына ие болады.
нөлден өзгеше мәнге ие болса, онда қосымша анизотропиялық энергия шамасы пайда болады. Осы уақытта электронның ядроны айнала қозғалатын тұйық орбитасы деформацияланып, шеңбер орнына элипс формасына ие болады.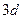 металдарда) спин-орбиталдық өзара әсерлесу энергиясынан үлкен болса, онда
металдарда) спин-орбиталдық өзара әсерлесу энергиясынан үлкен болса, онда 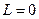 нөлге тең болады да, ол қозғалмайды.
нөлге тең болады да, ол қозғалмайды.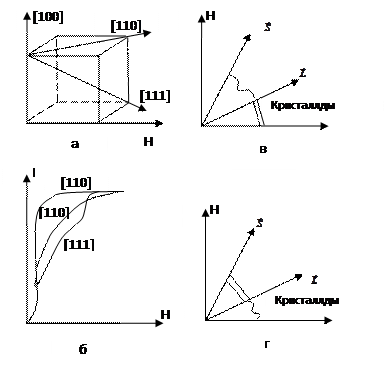
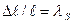 байқалады. Бұл құбылысты магнитострикция деп атайды.
байқалады. Бұл құбылысты магнитострикция деп атайды.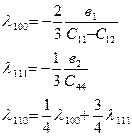 (2.68)
(2.68)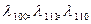 куб торына ие болатын ферро- магнетиктер үшін сәйкесті магниттелу бағыттарына сәйкес келетін магнитострикция коэффициенттері.
куб торына ие болатын ферро- магнетиктер үшін сәйкесті магниттелу бағыттарына сәйкес келетін магнитострикция коэффициенттері.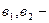 магниттің серпімділік тұрақтылары,
магниттің серпімділік тұрақтылары,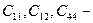 серпімділік модульдері.
серпімділік модульдері.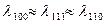 магнитострикция коэффициенттері бір-біріне тең болса, онда бұндай магнитострикция құбылысын изотропты магнитострикция деп атайды.
магнитострикция коэффициенттері бір-біріне тең болса, онда бұндай магнитострикция құбылысын изотропты магнитострикция деп атайды.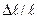 шамасы мынадай өрнек арқылы есептелінеді:
шамасы мынадай өрнек арқылы есептелінеді: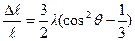 (2.69)
(2.69)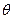 - магниттеу бағытымен өлшеу бағытының арасын-дағы бұрыш.
- магниттеу бағытымен өлшеу бағытының арасын-дағы бұрыш.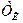 температурасынан жоғары тұрған ферро-магнитті сфера формалы үлгі;
температурасынан жоғары тұрған ферро-магнитті сфера формалы үлгі;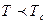 температура кезінде изотропиялық алмасу магнитострикция есебінен үлгінің көлемінің өзгеруі;
температура кезінде изотропиялық алмасу магнитострикция есебінен үлгінің көлемінің өзгеруі;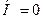 кездегі
кездегі 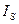 бұратын магнит өрісі
бұратын магнит өрісі 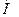 оны кристаллографиялық ось бағытында эллипсоиданың осінің бағытына бағыттас етіп (2.21,г- сурет) бұрады. Осы құбылыс магнитострикциялық деформациясының кристаллографиялық осьтерінің бағытында әртүрлі мәнді қабылдауына жауапты болып табылады.
оны кристаллографиялық ось бағытында эллипсоиданың осінің бағытына бағыттас етіп (2.21,г- сурет) бұрады. Осы құбылыс магнитострикциялық деформациясының кристаллографиялық осьтерінің бағытында әртүрлі мәнді қабылдауына жауапты болып табылады.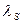 бағаланады.
бағаланады.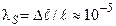 ал сирек кез- десетін
ал сирек кез- десетін 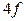 металдар үшін
металдар үшін 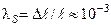 мәндеріне ие болады.
мәндеріне ие болады.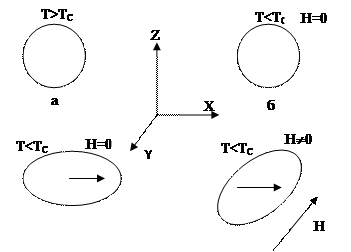
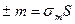 ) деп жориық.2.22- сурет.
) деп жориық.2.22- сурет.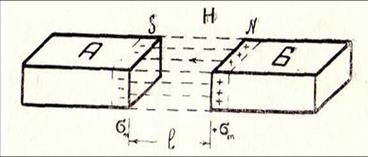
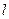 аралыққа ажырату үшін белгілі бір жұмыс жасау қажет
аралыққа ажырату үшін белгілі бір жұмыс жасау қажет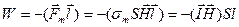
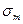 сан жағынан магниттелу векторына тең болады.
сан жағынан магниттелу векторына тең болады.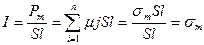
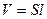 қатынасы немесе энергия тығыздығы
қатынасы немесе энергия тығыздығы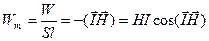 (2.70)
(2.70)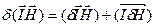 (2.71)
(2.71)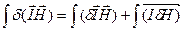 (2.72)
(2.72)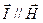 бағыттары бірдей болса, онда (2.72) теңдеуді мынадай түрде жазуға болады
бағыттары бірдей болса, онда (2.72) теңдеуді мынадай түрде жазуға болады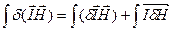 (2.73)
(2.73)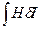 - магниттеу жұмысы, ал
- магниттеу жұмысы, ал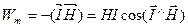
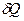 жылуы жүйенің ішкі энергиясын
жылуы жүйенің ішкі энергиясын 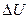 өзгертуге және сыртқы күштерді жеңуге
өзгертуге және сыртқы күштерді жеңуге 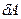 жұмсалады.
жұмсалады.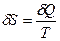 (2.74)
(2.74)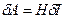 (2.75)
(2.75)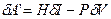 (2.76)
(2.76)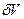 - магниттің көлемінің өзгерісі. Бұл қатынастарда басқа термодинамикалық функциялар:
- магниттің көлемінің өзгерісі. Бұл қатынастарда басқа термодинамикалық функциялар: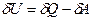 теңдеуіне қойсақ онда
теңдеуіне қойсақ онда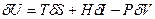 (2.80)
(2.80)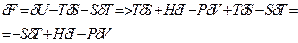 (2.81)
(2.81)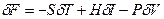 (2.82)
(2.82)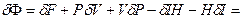
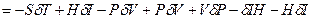
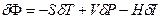 (2.83)
(2.83)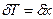 ,
, 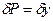 ,
, 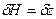 белгілесек (2.84)
белгілесек (2.84)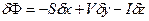 (2.85)
(2.85)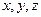 айнымалылары бойынша бірінші және екінші ретті туындылары
айнымалылары бойынша бірінші және екінші ретті туындылары 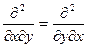 негізінде
негізінде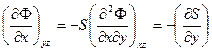 (a)
(a)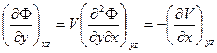 (б)
(б)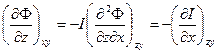 (в)
(в)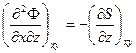 (г)
(г)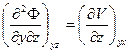 (д)
(д)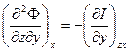 (ж)
(ж)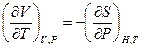 (2.86)
(2.86)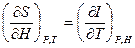 (2.87)
(2.87)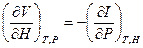 (2.88)
(2.88)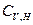 ;
; 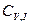 ;
; 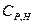 ;
; 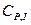 деп бөледі. Тұрақты магнит өрісінің кернеуі мен магниттелуі кезінде
деп бөледі. Тұрақты магнит өрісінің кернеуі мен магниттелуі кезінде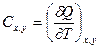 (2.89)
(2.89)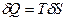 еске алсақ, онда (2.89) теңдеу мынадай түрге ие болады.
еске алсақ, онда (2.89) теңдеу мынадай түрге ие болады. (2.90)
(2.90)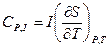 ;
; 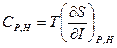 (2.91)
(2.91)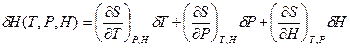 (2.92)
(2.92)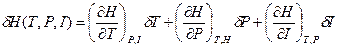 (2.93)
(2.93) (2.94)
(2.94)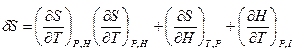 (2.95)
(2.95)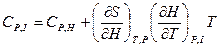 (2.96)
(2.96)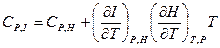 (2.97)
(2.97)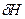 магнит өрісін өзгерткен кезде магнит
магнит өрісін өзгерткен кезде магнит 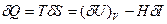
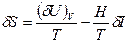 (2.98)
(2.98)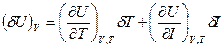 (2.99)
(2.99)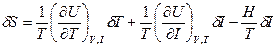
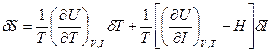 (2.100)
(2.100)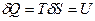
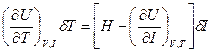 (2.101)
(2.101)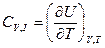 (2.102)
(2.102)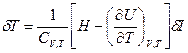 (2.103 )
(2.103 )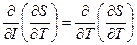 пайдалана отырып, (2.100) теңдеуден
пайдалана отырып, (2.100) теңдеуден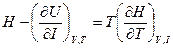 (2.104)
(2.104)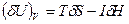 (2.105)
(2.105)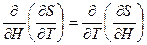 теңдеуді пайдаланып,
теңдеуді пайдаланып,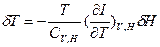 (2.106)
(2.106)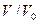 жазсақ онда термодинамикалық потенциал мынадай түрде өзгереді.
жазсақ онда термодинамикалық потенциал мынадай түрде өзгереді.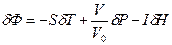 (2.107)
(2.107)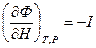 ,
, 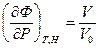
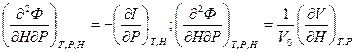
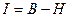 өрнегін пайдалана отырып, жоғарыдағы термодинамикалық потенциал теңдеуінен, меншікті жылу сыйымдылықтың магниттелу векторы мен магнит өрісінің кернеулігін есептеген тәрізді магнитострикция коэффициентінің магнит өрісін сипаттайтын параметрлерге тәуелділігін мына өрнектер арқылы есептеуге болады. .
өрнегін пайдалана отырып, жоғарыдағы термодинамикалық потенциал теңдеуінен, меншікті жылу сыйымдылықтың магниттелу векторы мен магнит өрісінің кернеулігін есептеген тәрізді магнитострикция коэффициентінің магнит өрісін сипаттайтын параметрлерге тәуелділігін мына өрнектер арқылы есептеуге болады. .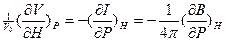 (2.108)
(2.108)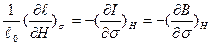 (2.109)
(2.109)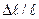 салыстырмалы ұзару мен Юнг модулі азаяды да
салыстырмалы ұзару мен Юнг модулі азаяды да 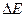 - эффект пайда болады.
- эффект пайда болады. 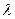 магнитострикцияға пайда болған кезде ғана пайда болатындықтан көпшілік ферромагниттік қасиетке ие болатын қорытпаларда (мысалы Fe-Ni)
магнитострикцияға пайда болған кезде ғана пайда болатындықтан көпшілік ферромагниттік қасиетке ие болатын қорытпаларда (мысалы Fe-Ni) 



