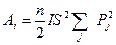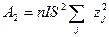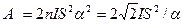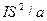Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заттың магниттік қасиетіне әсер ететін энергияларСодержание книги
Поиск на нашем сайте
2. Заттың магниттік қасиетіне әсер ететін энергиялар 2.1 Өзара әсерлесудің алмасу энергиясы. Магнитті кристалдардың тосын магниттелу моменттерін түсіндіру үшін Розинг пен Вейсс
мұндағы Темір кристалы үшін
осындай үлкен өрісте орналасқан ферромагниттердің ~10 Жоғарыда (2.1) теңдеу арқылы анықталатын Вейстің молекулалық өрісін жүйедегі классикалық диполь туғызатын ішкі өрістен аздаған шамаға үлкен болатындығын дәлелдеуге бола-ды. Бұл өрістің пайда болуын алмасу күшінің электростатикалық сипатқа ие болатындығының кванттық механикалық негізде Паули принципіне байланыстыра отырып түсіндіреді. Гейзенберг-Дирак моделінің шеңберінде кристалдық тордың і-ші
түйінінде орналасқан атомды толық спиннің операторы
Мұндағы
Мұндағы қосу амалы жақын орналасқан атомдар жұбы арқылы жүргізіледі. Көрші параллель спиндердің параллель бағытталуынан сәл ауытқыған жағыдайларында алмасу энергиясын квазиклас-сикалық жуықтау әдісіне сүйене отырып, спиндік операторларды классикалық векторлармен алмастыру арқылы мынадай түрде жазуға болады
Мұндағы
Мұндағы
Немесе
Сонда
Енді (2.4) өрнектің қалған екі қосылғышын (2.7) теңдеу түрінде жазуға болады.
Қорытындысында,
Жіктеудің жоғары дәрежелерін еске алмасақ, онда алмасу энрегиясын
Бұл (2.9) өрнек біртекті магниттелетін (ақаусыз кристалл үшін) алмасу энергиясының өсуін сипаттайды. Бірдей спиндер жүйесін үшін бір өлшем көлемге келетін алмасу энергиясының тығыздығын анықтау үшін қосуды көршілес түйіндер арқылы жүргізіп, көршілер арасындағы өзара әсерлесулерді екі рет есептемеу үшін ½ «факторын» коэффициентін енгізіп, көлем бірлігі ішіндегі спиндер саны n көбейтеміз. Кубтық кристалдық торға ие болатын кристалдар үшін
Енді (2.9) теңдеуіндегі тұрақты шамаларды ескермей жаза-тын болсақ, онда
Мұндағы
Қарапайым көлемге ортақталған кубтық торлар үшін
Кубтық ортаға ортақталған кубтық және жаққа ортақталған кубтық кристалдық торлар үшін с=1.2 және 4 тең сәйкесті мәндерді қабылдайды. Гексогональдық сингонияға ие болатын кристалдық тор-лары үшін
Мұндағы
Гексоганальды тығыз орналастырылған кристалл үшін (2.12) және (2.10) өрнектерін
Мұндағы а- жақын көршілес атомдардың арақашық-тықтары. Осындай жолмен басқа да кристалдық торлар тектері (тетроганальдық, тригональдық, ромбалық, моноклиндік, три-клиндік) үшін де алмасу энергиясын есептеуге болады.
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.51 (0.009 с.) |

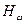 ішкі күшті молекулалық магнит өрісі болатындығы туралы гипотезаны ұсынды. Бұл өріс сыртқы магнит өрісінің кернеулігі
ішкі күшті молекулалық магнит өрісі болатындығы туралы гипотезаны ұсынды. Бұл өріс сыртқы магнит өрісінің кернеулігі 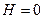 тең болғанда атомдардың магнит моменттерін бір- біріне параллель орналас-тыруға тырысады. Атомдық магнит моменттердің
тең болғанда атомдардың магнит моменттерін бір- біріне параллель орналас-тыруға тырысады. Атомдық магнит моменттердің 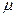 ішкі молекулалық өріспен
ішкі молекулалық өріспен 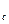 кезінде ондаған есе көп болуы керек.
кезінде ондаған есе көп болуы керек.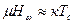 (2.1)
(2.1)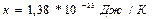 - Больцман тұрақтысы,
- Больцман тұрақтысы, 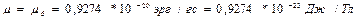 .
.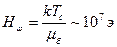
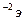 сыртқы магнит өрісінде тосын магниттелуін түсіндіру үшін оларды жеке домендерге (тосын магниттелген аймақтарға бөлу) ұсынылды.
сыртқы магнит өрісінде тосын магниттелуін түсіндіру үшін оларды жеке домендерге (тосын магниттелген аймақтарға бөлу) ұсынылды.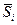 ар-қылы сипаттауға болады. Сонда электрондар жүйесінің энергия операторын белгілі бір аддитивті тұрақтыға дейін жуықтап магниттік өзара әсерлесу күшін алмасақ, онда
ар-қылы сипаттауға болады. Сонда электрондар жүйесінің энергия операторын белгілі бір аддитивті тұрақтыға дейін жуықтап магниттік өзара әсерлесу күшін алмасақ, онда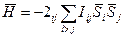 (2.2)
(2.2)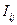 - атомдық алмасу интегралы. Ол кристалдық тордың түйіндерінде орналасқан атомдардың электрондық қа-баттарының бірін- бірі жабуы нәтижесінде электрондық спин-дерінің параллель және антипараллель орналасу нәтижесінде пайда болатын кулондық өзара әсерлесудің айырмашылығын сипаттайды. Бұл интегралдың шамасы i және j атомдарының арақашықтығына тәуелді болады. Сонда (2.2) теңдеудің орнына
- атомдық алмасу интегралы. Ол кристалдық тордың түйіндерінде орналасқан атомдардың электрондық қа-баттарының бірін- бірі жабуы нәтижесінде электрондық спин-дерінің параллель және антипараллель орналасу нәтижесінде пайда болатын кулондық өзара әсерлесудің айырмашылығын сипаттайды. Бұл интегралдың шамасы i және j атомдарының арақашықтығына тәуелді болады. Сонда (2.2) теңдеудің орнына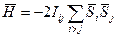 (2.3)
(2.3)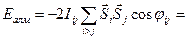
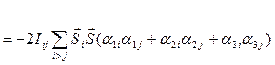 (2.4)
(2.4)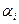 және
және 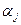 сәйкесті
сәйкесті 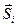 және
және 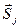 векторларының бағыттаушы косинустары. Енді бағыттаушы косинустардың ко-ординаталардың функциясы екендігін ескере отырып, Тейлор қатарына жіктеуді қолданатын болсақ, онда
векторларының бағыттаушы косинустары. Енді бағыттаушы косинустардың ко-ординаталардың функциясы екендігін ескере отырып, Тейлор қатарына жіктеуді қолданатын болсақ, онда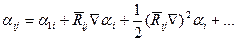 (2.5)
(2.5)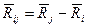 i-ші және j-ші түйіндер аралығы. Бұдан
i-ші және j-ші түйіндер аралығы. Бұдан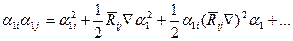 (2.6)
(2.6)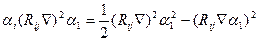
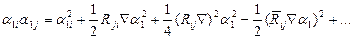 ( 2.7)
( 2.7)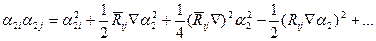
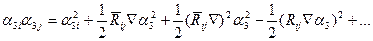
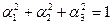 ескере отырып
ескере отырып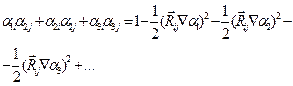 (2.8)
(2.8)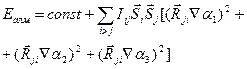 (2.9)
(2.9)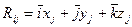 , ал
, ал 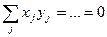 және
және 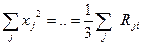
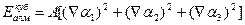 (2.10)
(2.10)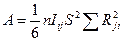
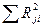 сәйкесті
сәйкесті 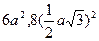 және 12
және 12 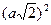 , яғни әрбір жағыдай үшін
, яғни әрбір жағыдай үшін 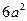 тең болады. Сонда қарастырып отырған кристалдық торлар үшін көлем бірлігіне келетін спиндер саны: 1/
тең болады. Сонда қарастырып отырған кристалдық торлар үшін көлем бірлігіне келетін спиндер саны: 1/ 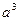 , 2/
, 2/ 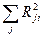 сәйкесті 6/а, 12/а және 24/а мәндерге ие болады. Қортындысында алмасу параметрлерінің мәнін жалпы түрде
сәйкесті 6/а, 12/а және 24/а мәндерге ие болады. Қортындысында алмасу параметрлерінің мәнін жалпы түрде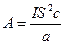 (2.11)
(2.11)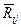 векторының базалық жазықтыққа проекциясын
векторының базалық жазықтыққа проекциясын 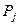 арқылы, ал
арқылы, ал 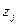 арқылы гексагоальдық оське проекциясын белгілесек, онда алмасу энергиясының тығыздығы
арқылы гексагоальдық оське проекциясын белгілесек, онда алмасу энергиясының тығыздығы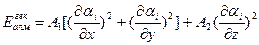 (2.12)
(2.12)