Куб кристалының серпімді энергиясы
Деформацияланбаған кристалды бір жақты деформа- циялаған кезде оның бірлік векторлары 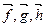 үш ортогонал осьтердің бойында үш ортогонал осьтердің бойында 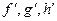 жаңа мәндерге ие болсын деп жориық. жаңа мәндерге ие болсын деп жориық.
Мұндағы 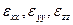 шамалары шамалары 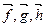 векторларының ұзындықтарының салыстырмалы өзгерістерін береді. Енді деформация тензорларының векторларының ұзындықтарының салыстырмалы өзгерістерін береді. Енді деформация тензорларының 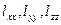 құраушыларын құраушыларын 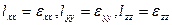 арқылы анықтайық. арқылы анықтайық.
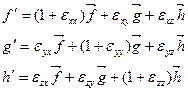
Ал аралас құраушыларын 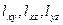 бірінші ретті дәлдікке дейін осьтер арасындағы бұрыштардың өзгерістері арқылы анықтауға болады. бірінші ретті дәлдікке дейін осьтер арасындағы бұрыштардың өзгерістері арқылы анықтауға болады.
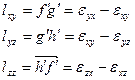
lij анықтау үшін деформация тензорының алты құраушысын анықтау жеткілікті.
Жүктеме немесе бір өлшем бетке әсер ететін күш, аз деформация мөлшері үшін Гук заңы бойынша оған сызықтық байланыста болады. Екінші ретті тензор құраушыларының арасындағы сызықтық байланысты Гук заңының кеңейтілген түрінде мынадай түрде жазуға болады.
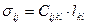
Мұндағы σij - симметриялы (σij= σjll) жүктеме тензоры, ал 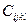 коффициенті төртінші рангалы 34=81 құраушыға ие болатын тензор түзейді. Деформация шамасы dl өте аз шамаға ие болған кезде жүктеме жұмыс жасайды. коффициенті төртінші рангалы 34=81 құраушыға ие болатын тензор түзейді. Деформация шамасы dl өте аз шамаға ие болған кезде жүктеме жұмыс жасайды.
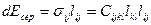
Ал энергияның тығыздығы осы өрнектен алынған интегралға тең болады.
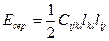
Куб кристалы үшін тәуелсіз тұрақты шама ретінде тек үш шаманы алады.
Ciiii = C11, Ciijj = C12, Cijij = C44 (2.37)
Кристалдың симметрия қасиетіне сүйене отырып, 90° бұрғанда инвариантты болатындығын ескере келе серпімді энергияны
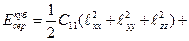
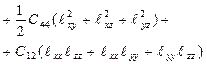 (2.37а) (2.37а)
Мұндағы Cij - серпімділік модулі, lij -деформация. Бұл шама магниттелудің 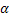 косинусының бағытына тәуелсіз болады. косинусының бағытына тәуелсіз болады.
Серпімділік модулінің темір кристаллы үшін мәні
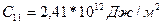
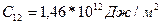
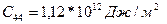
Ал никель үшін
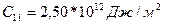
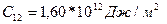
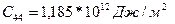
|