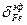Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитострикцияның 180°-тық домен шекаралығы энергиясына әсеріСодержание книги
Поиск на нашем сайте
Енді куб кристалдарындағы домен шекаралығының энергиясы мен енін анықтайық. Домен шекаралығының қалыптасуына алмасу және магнитокристаллографиялық энергиялармен бірге магнитосерпімділік өзара әсерлесу энергиясы да әсер етеді. Куб кристалындағы деформация тензорының (2.39) құраушыларын (2.40) (2.41) өрнектерді ескере отырып,
Бұл өрнектен Сонда серпімді дененің тепе- теңдік теңдеуді жалпы түрде
бұдан Сондықтан домен шекаралығының басы артық магнито-серпімділік энергиясын Енді куб кристалдарындағы 180°-тық домен шекаралығын Сонда деформация тензорының құраушысын (2.64) мынадай түрде жазуға болады.
Жоғары келтірілген 2.10- суреттегі домен шекаралығы үшін
Яғни Шекаралық қабаттың қалыңдығы мен энергиясы (2.49) (2.50) бойынша анықталатын. Енді (2.62) ескере отырып
Бұл өрнектегі шамаларға мынадай белгілеулер енгізіп,
(2.65) теңдеуді қайтадан жазайық.
Сонда (2.49) теңдеуді интегралдау қорытындысын мы- надай түрге келеді
Шекара қалындығын есептеу үшін (2.50) өрнегін қол-данамыз. Интегралды есептегеннен кейін
Осындай жолмен куб кристалдарында жеңіл магниттелу осіне ие болатын 180 Кестеден магнитосерпімді энергия никель кристалында домен шекаралығының энергиясын біршама өзгертеді. Ал темір кристаллы үшін ескерерліктей шамаға ие болмайды.
2.10- кесте
Темір мен никель кристалдарындағы 180°-тық домен шекаралығының ені мен энергиясы. Салыстыру үшін жақша ішінде магнитострикцияның әсерінсіз есептелген мәндері келтірілген.
Шекаралыққа жүргізілген [001] [110] [
2,19 (1,8292 2,27 (2.0040
2,02 (2,000 2,78 (2,7808
7,91 4,45 (7,9161
10,87 5,59 (5,8018
Домен шекаралығының қалыңдығы (2.66) өрнегінен барлық магниттелу бағыттары үшін ескерерліктей мәнге ие. Оның шамасы Жеке оське ие болатын кобальт кристаллы үшін магнитострикция домен шекаралығымен оның қалыңдығына аса әсер ете қоймайды. Өйткені кобальттың магнитострикциясы никель мен темірге қарағанда ескерусіз аз шама, бірақ магнитокристаллографиялық анизатропиясы, темірдің аниза-тропия тұрақтысынан үлкен. Жеке оске ие болатын магнитті кристалдарда домен шекаралығы белгілі бір шекаралық қалыңдығына ие болып, магнитострикцияға тәуелсіз болады.
|
|||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 9; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.238.81 (0.008 с.) |

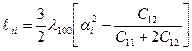 (2.64)
(2.64)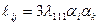
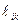 құраушы екі қарама- қарсы маг- ниттелген домен үшін өзара тең болады. Әрі қарай
құраушы екі қарама- қарсы маг- ниттелген домен үшін өзара тең болады. Әрі қарай 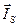 магниттелу векторының шекаралықта үлестірілуі тек бір ғана координатаға тәуелді болса, онда деформация тензоры да бірақ координатаға тәуелді болып, ал
магниттелу векторының шекаралықта үлестірілуі тек бір ғана координатаға тәуелді болса, онда деформация тензоры да бірақ координатаға тәуелді болып, ал 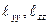 және
және 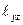
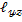 құраушылары тұрақты күйінде қалады.
құраушылары тұрақты күйінде қалады. , ол
, ол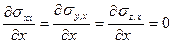 ,
,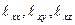 құраушыларының тұрақтылығы келіп шыға-ды. Сонымен 180°-тық домен шекаралығының деформациясы тұрақты және оның сан мәні шексіз жағыдай үшін есептелген мәндеріне тең болады.
құраушыларының тұрақтылығы келіп шыға-ды. Сонымен 180°-тық домен шекаралығының деформациясы тұрақты және оның сан мәні шексіз жағыдай үшін есептелген мәндеріне тең болады.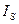 векторының бағыттаушы косинус-тарының мәнін қою арқылы есептейді.
векторының бағыттаушы косинус-тарының мәнін қою арқылы есептейді.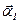 және
және 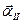 бағыттауыштары арқылы бөлінетін, ал
бағыттауыштары арқылы бөлінетін, ал 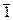 ] және [001] бағытталған (
] және [001] бағытталған ( 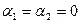
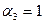 ).
).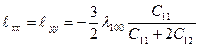 ,
,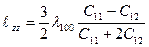 ,
,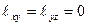
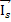 векторы [-
векторы [- 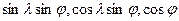 ] бұрыштарымен анықталады. Магнитосерпімді энергияның өсім- шесі
] бұрыштарымен анықталады. Магнитосерпімді энергияның өсім- шесі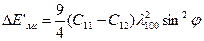
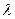 бұрышына тәуелсіз.
бұрышына тәуелсіз.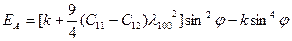 (2.65)
(2.65)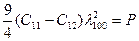
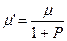
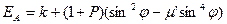
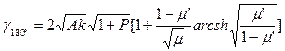
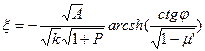 (2.66)
(2.66) -тық домен шекаралығының параметрлерін есептеулерді жүргізуге (2.10 кесте) болады.
-тық домен шекаралығының параметрлерін есептеулерді жүргізуге (2.10 кесте) болады.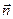 нормаль бағыттары
нормаль бағыттары ]
]
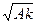
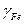
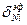
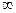 )
)