
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сыртқы жүктеме- кернеу энергиясыСодержание книги
Поиск на нашем сайте
2.14 Сыртқы жүктеме- кернеу энергиясы Магниттік қасиетке ие болатын денелерге сырттан күш түсірілген кезде, онда пайда болатын қосымша энергияны тензор түрінде жазады
Мұндағы Uik - магнитострикция және сыртқы жүктемелер тудыратын серпімді деформация тензоры. Куб кристаллдары үшін біртекті жүктеме кезінде
Мұндағы σ - сыртқы жүктеме кернеу, ал
Бұл энергияның шамасы сырттан түсірілген σ жүктеме- кернеудің шамасына немесе табиғи кристаллографиялық анизатропия кезінде үлкен шамаға (λSσ>>>k) ие болады. Изотропты кристалл үшін (2.45)
Мұндағы θ бұрышы магниттелу векторы
2.15 Тұтас ферромагнитті кристалдардағы жазық домен шекаралықтары. Ферромагнитті кристалдарда тосын магниттелудің та- ралуын есептеу (домендердің өлшемімен форма - пішіні мен олардың аралығындағы шекаралықтарды анықтау) жүйенің потенциалдық энергиясының жиынтығын «минимизациялай» отырып вариациялық есептерді шешу жолымен жүргізілуі қажет. Вариациялық есептерді шешу сызықтық емес дербес туындылардан тұратын дифференциялдық теңдеулер жүйесіне әкеледі. Бұл теңдеулерді интегралдау өте қиын болғандықтан олардың аналитикалық шешімдерімен кейбір дербес жағыдайлар үшін ғана алынған. Ландау мен Лифшиц домен құрлысының жалпы мәсе- лелерін өте үлкен дәлдікке ие болатын бір- біріне тәуелсіз екі есепке (мәселеге) бөліп қарастыруды ұсынады. Олар: а) домен шекаралығындағы тосын магниттелу векторының таралуы; б) шекаралық қабаттардағы Сонымен мәселені осылай шешуге бару домен құры- лымының барлығы «постулаттанады», оның құрылымының маңызды параметрлерін есептеуге мүмкіндік ашады. Ең қарапайым жағыдайда жалқы (жеке) осьті кристалды магнитсіздендіру домен аралық шекараны екі антипараллель магниттелген фазалық облысқа бөледі. Әрбір фаза жеңіл магнит-телу осінің бойында біртекті магниттеледі. Сондықтан бұл фаза-лардың ішінде алмасу энергиясымен анизатропия энергиялары ең аз шамаға ие болады. Магниттелу векторын фазалар шекараларында 180° яғни +IS -тен -IS дейін ауыстыру магниттелудің біртектілігін бұзады да, оң алмасу энергиясының шамасын арттырады. Бұл жағыдай-да спиндердің бағыты бір атомдық жазықтықтан екінші атом-дық жазықтыққа бірден 180° бұрылса (2.6 сурет) онда бұндай шарт магнитокристаллографиялық энергияның Егер кристалдық торының тұрақтысы а тең болатын куб кристалының симметриясын еске алатын болсақ, онда шекара-лықтың екі жағының бір өлшеміне 1/
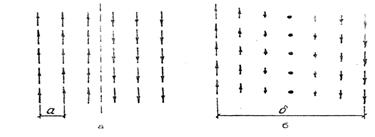
Талап етіп отырған бұрыштың өзгерісі N табалдырық арқылы іске асырылса, онда (2.6 б- сурет) көршілес спиндер аралығындағы бұрыш π/N тең болады. Сонда көршілес жұп спиндер үшін алмасу энергиясы
2.6-сурет. Домен шекаралығындағы спиндердің бұрылуын бейнелейтін сүлбе яғни γалм энергиясы Сонымен алмасу энергиясының ең аз шамасы магниттелу векторын атомдық қабаттарда бұрудың басты шарты болып табылады.
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.79.188 (0.009 с.) |

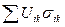 (i,k=x,y,z)
(i,k=x,y,z)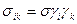 (i,k=x,y,z)
(i,k=x,y,z)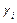 кристал осіне қатысты оның бағыттаушы косинусы.
кристал осіне қатысты оның бағыттаушы косинусы.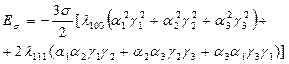 (2.45)
(2.45)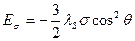
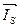 мен біртекті жүктеме - кернеу бағыты арасындағы бұрыш.
мен біртекті жүктеме - кернеу бағыты арасындағы бұрыш.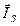 магниттелу векторының сыртқы факторлардың әсерінен таралуы .
магниттелу векторының сыртқы факторлардың әсерінен таралуы .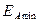 шартын өзгертпейді. Ол оң алмасу энергиясының пайда болуына жол ашады. Бұл жағыдайда екі көршілес спиндер аралығының екі жағында шекаралық бір - біріне тең және (2.4) теңдеуге сәй-кесті +2IS2 алмасу энергиясы пайда болады.
шартын өзгертпейді. Ол оң алмасу энергиясының пайда болуына жол ашады. Бұл жағыдайда екі көршілес спиндер аралығының екі жағында шекаралық бір - біріне тең және (2.4) теңдеуге сәй-кесті +2IS2 алмасу энергиясы пайда болады.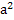 спиндер жұбы келеді. Сонда бір өлшем шекаралық ауданға келетін жалпы энергия
спиндер жұбы келеді. Сонда бір өлшем шекаралық ауданға келетін жалпы энергия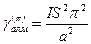
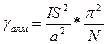
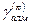 энергиясын (180° - шекаралық келетін) энергиядан N есе аз болады.
энергиясын (180° - шекаралық келетін) энергиядан N есе аз болады.


